常见排序--归并排序（递归和非递归）+计数排序

4 归并排序

基本思想：
归并排序（MERGE-SORT）是建立在归并操作上的一种有效的排序算法,该算法是采用分治法（Divide andConquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。 归并排序核心步骤：(其实就是一个后序排序，先分解到一个有序再合并)

4.1 递归形式

难点在于合并：举个简单例子：就是两个数组合并成一个有序的数组方法类似
方法：就是两个数组一个一个数比大小，小的拿下来（我们需要一个额外的数组-叫tmp来实现），存在tmp数组中拿下来的数组往后移动到下一个数，然后我们可以至少保证有一个数组被拿完，剩下的我们依次拿下来，最后再把tmp赋给原来的数组中。
(begin1: 和begin2：是两个数组的开头。 )
这一块这样实现：

int begin1 = left, begin2 = mid + 1;
	int end1 = mid, end2 = right;
	int i = begin1; //begin1不一定是0
	while (begin1<=end1 && begin2 <= end2)
	{
    
		if (a[begin1] <= a[begin2])
		{
    
			tmp[i++] = a[begin1++];
		}
		else
		{
    
			tmp[i++] = a[begin2++];
		}

	}

	//三种可能。1.左半部分走完了，右半部分未走完。2.右半部分走完了，左半部分未走完。
	//3.都走完了。我们其实不用关心，谁还剩下。
	while (begin1 <= end1)
	{
    
		tmp[i++] = a[begin1++];
	}

	while (begin2 <= end2)
	{
    
		tmp[i++] = a[begin2++];
	}

	memcpy(a + begin, tmp + begin, (end - begin + 1) * sizeof(int));
}

注意：最后tmp需要释放。
代码块：

void _mergeSort(int* a, int begin,  int end, int* tmp)
{
    
	assert(a);

	if (begin >= end)
		return;

	int left = begin;
	int right = end;
	int mid = left + (right - left) / 2;//（right+left）/2

	_mergeSort(a, left, mid, tmp);
	_mergeSort(a, mid + 1, right, tmp);

	int begin1 = left, begin2 = mid + 1;
	int end1 = mid, end2 = right;
	int i = begin1; //begin1不一定是0
	while (begin1<=end1 && begin2 <= end2)
	{
    
		if (a[begin1] <= a[begin2])
		{
    
			tmp[i++] = a[begin1++];
		}
		else
		{
    
			tmp[i++] = a[begin2++];
		}

	}

	//三种可能。1.左半部分走完了，右半部分未走完。2.右半部分走完了，左半部分未走完。
	//3.都走完了。我们其实不用关心，谁还剩下。
	while (begin1 <= end1)
	{
    
		tmp[i++] = a[begin1++];
	}

	while (begin2 <= end2)
	{
    
		tmp[i++] = a[begin2++];
	}

	memcpy(a + begin, tmp + begin, (end - begin + 1) * sizeof(int));
}

void MergeSort(int* a, int n)
{
    
	assert(a);

	int* tmp = (int*)calloc(n, sizeof(int));
	if (tmp == NULL)
	{
    
		printf("calloc fail");
		exit(-1);
	}

	_mergeSort(a, 0, n - 1, tmp);

	free(tmp);
}

4.2非递归形式

非递归说白了我们直接从合并那一步开始，我们手搓一个递归形成。

非递归排序与递归排序相反，将一个元素与相邻元素构成有序数组，再与旁边数组构成有序数组，直至整个数组有序。
要有mid指针传入，因为不足一组数据时，重新计算mid划分会有问题需要指定mid的位置
图有助于理解：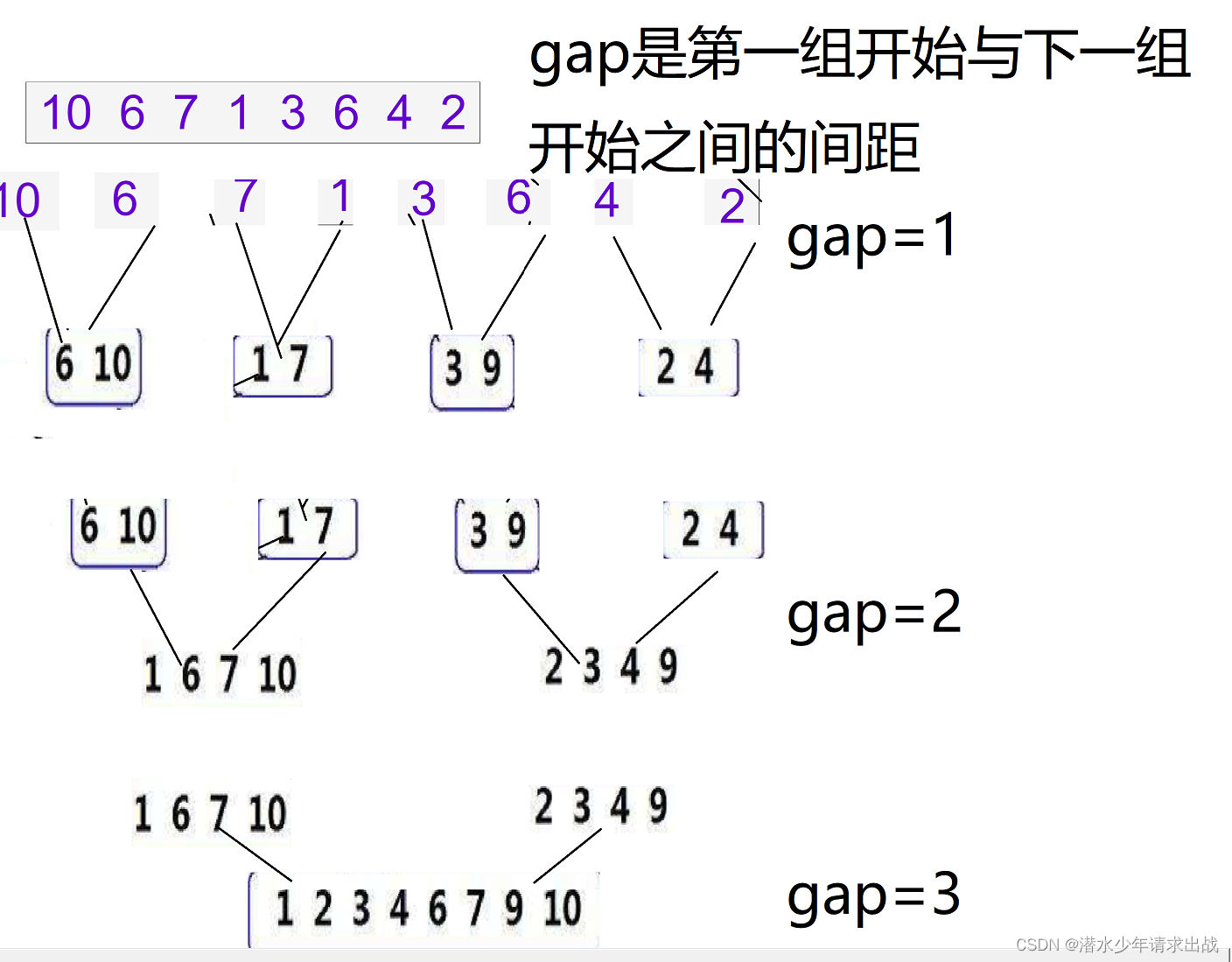

到这一步了，这不就简单 我们先看下面一段代码

void MergeSortNonR(int* a, int n)
{
    
	assert(a);

	int* tmp = (int*)calloc(n, sizeof(int));
	if (tmp == NULL)
	{
    
		printf("calloc fail");
		exit(-1);
	}
	int gap = 1;
	while (gap < n)
	{
    
		for (int i = 0; i < n; i += 2 * gap)
		{
    
			int begin1 = i, begin2 = i + gap;
			int end1 = i + gap - 1, end2 = i + 2 * gap - 1;
			
			int j = begin1;
			while (begin1 <= end1 && begin2 <= end2)
			{
    
				if (a[begin1] <= a[begin2])
				{
    
					tmp[j++] = a[begin1++];
				}
				else
				{
    
					tmp[j++] = a[begin2++];
				}

			}

			//三种可能。1.左半部分走完了，右半部分未走完。2.右半部分走完了，左半部分未走完。
			//3.都走完了。我们其实不用关心，谁还剩下。
			while (begin1 <= end1)
			{
    
				tmp[j++] = a[begin1++];
			}

			while (begin2 <= end2)
			{
    
				tmp[j++] = a[begin2++];
			}
		}

		memcpy(a, tmp, n * sizeof(int));

		gap *= 2;

	}

	free(tmp);
}

有问题吗？
先看一张每组的begin和end的范围图：

我们清晰的发现了，它越界了。

int begin1 = i, begin2 = i + gap;
int end1 = i + gap - 1, end2 = i + 2 * gap - 1;

我们可以知道begin1不会越界，其它都有可能。这个时候我们需要修边。（注意不要把越界的都改为n-1，这样可能会导致我们最后从tmp复制回去就丢失数据了）
操作：我们可以让它范围不成立或只有一个值

//修边
			if (end1 >= n)
			{
    
				end2 = end1 = n - 1;
				begin2 = n;
			}
			else if (begin2 >= n)
			{
    
				end2 = n - 1;
				begin2 = n;
			}
			else if (end2 >= n)
			{
    
				end2 = n - 1;
			}

综上可得
代码块：

void MergeSortNonR(int* a, int n)
{
    
	assert(a);

	int* tmp = (int*)calloc(n, sizeof(int));
	if (tmp == NULL)
	{
    
		printf("calloc fail");
		exit(-1);
	}

	int gap = 1;
	while (gap < n)
	{
    
		for (int i = 0; i < n; i += 2 * gap)
		{
    
			int begin1 = i, begin2 = i + gap;
			int end1 = i + gap - 1, end2 = i + 2 * gap - 1;

			//修边
			if (end1 >= n)
			{
    
				end2 = end1 = n - 1;
				begin2 = n;
			}
			else if (begin2 >= n)
			{
    
				end2 = n - 1;
				begin2 = n;
			}
			else if (end2 >= n)
			{
    
				end2 = n - 1;
			}

			int j = begin1;
			while (begin1 <= end1 && begin2 <= end2)
			{
    
				if (a[begin1] <= a[begin2])
				{
    
					tmp[j++] = a[begin1++];
				}
				else
				{
    
					tmp[j++] = a[begin2++];
				}

			}

			//三种可能。1.左半部分走完了，右半部分未走完。2.右半部分走完了，左半部分未走完。
			//3.都走完了。我们其实不用关心，谁还剩下。
			while (begin1 <= end1)
			{
    
				tmp[j++] = a[begin1++];
			}

			while (begin2 <= end2)
			{
    
				tmp[j++] = a[begin2++];
			}
		}

		memcpy(a, tmp, n * sizeof(int));

		gap *= 2;

	}

	free(tmp);
}

5计数排序

这个借助哈希桶部分性质，其实没什么。
这个实用于小范围集中重复的整数部分。我们需要借助一个数组来完成–tmp。
（简单理解就是我们把每个数的值就是一个下标，我们把这个数出现几次就在tmp数组下标所存的数就是几。负数就不适合）
思路：实际上，我们可以把最小的整数存再第一个。怎么做哪？对我们可以每个数减去最小值–这样既保证了负数可以存也杜绝空间浪费。最后我们再依次取出就可以了

void CountSort(int* a, int n)
{
    
	assert(a);

	int min = a[0], max = a[0];
	for (int i = 1; i < n; ++i)
	{
    
		if (min > a[i])
			min = a[i];
		
		if (max < a[i])
			max = a[i];
	}

	int range = max - min + 1;

	int* tmp = (int*)calloc(range, sizeof(int));
	if (tmp == NULL)
	{
    
		printf("calloc fail");
		exit(-1);
	}

	for (int i = 0; i < n; ++i)
	{
    
		tmp[a[i] - min]++;
	}

	int i = 0;
	for (int j = 0; j < range; ++j)
	{
    
		while (tmp[j]--)
		{
    
			a[i++] = j + min;
		}
	}

	free(tmp);
}

6总结

运行截图：

排序算法复杂度及稳定性分析：