Find the nearest common ancestor (Sword finger offer) of two nodes in the binary tree (search tree)

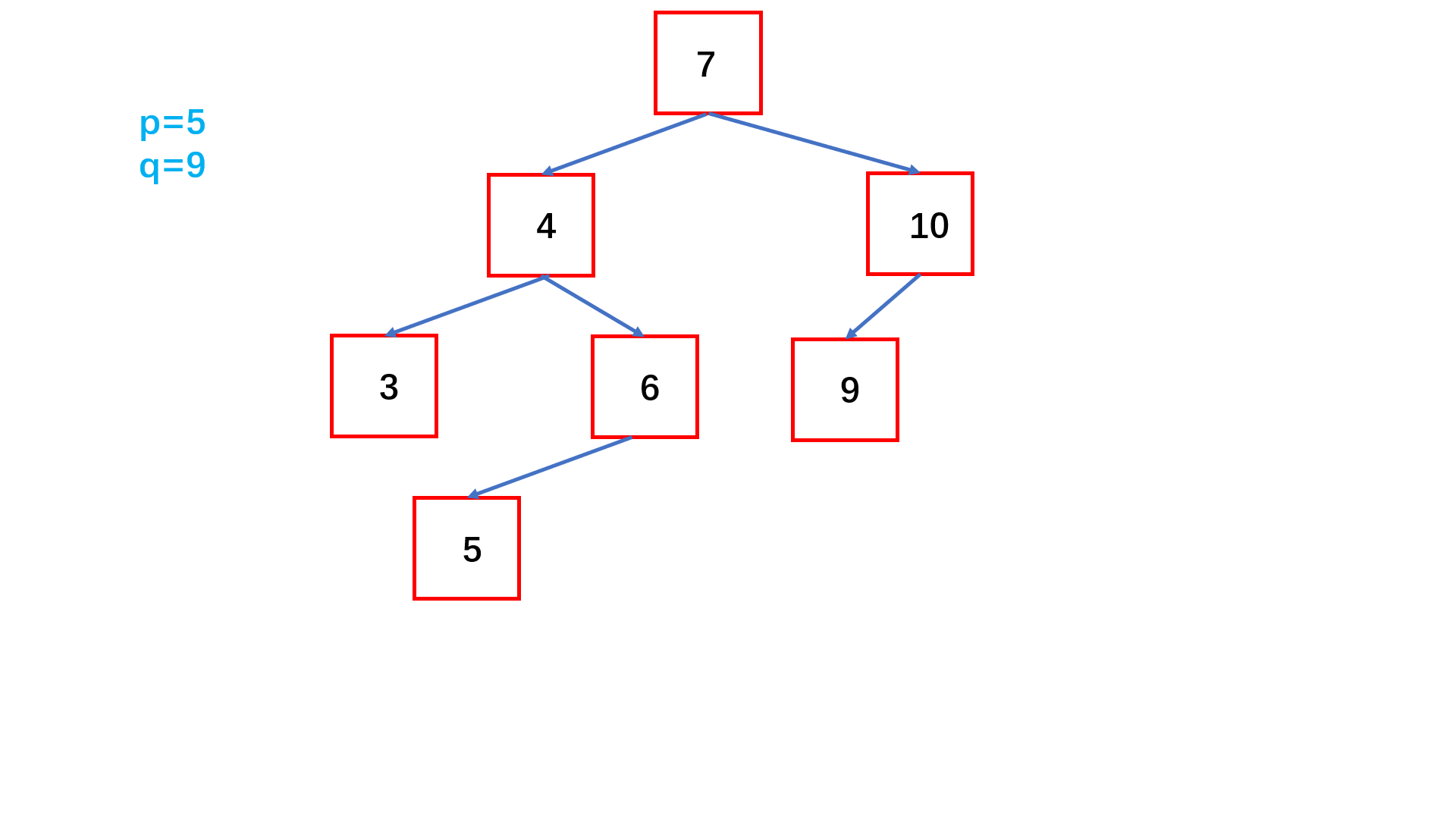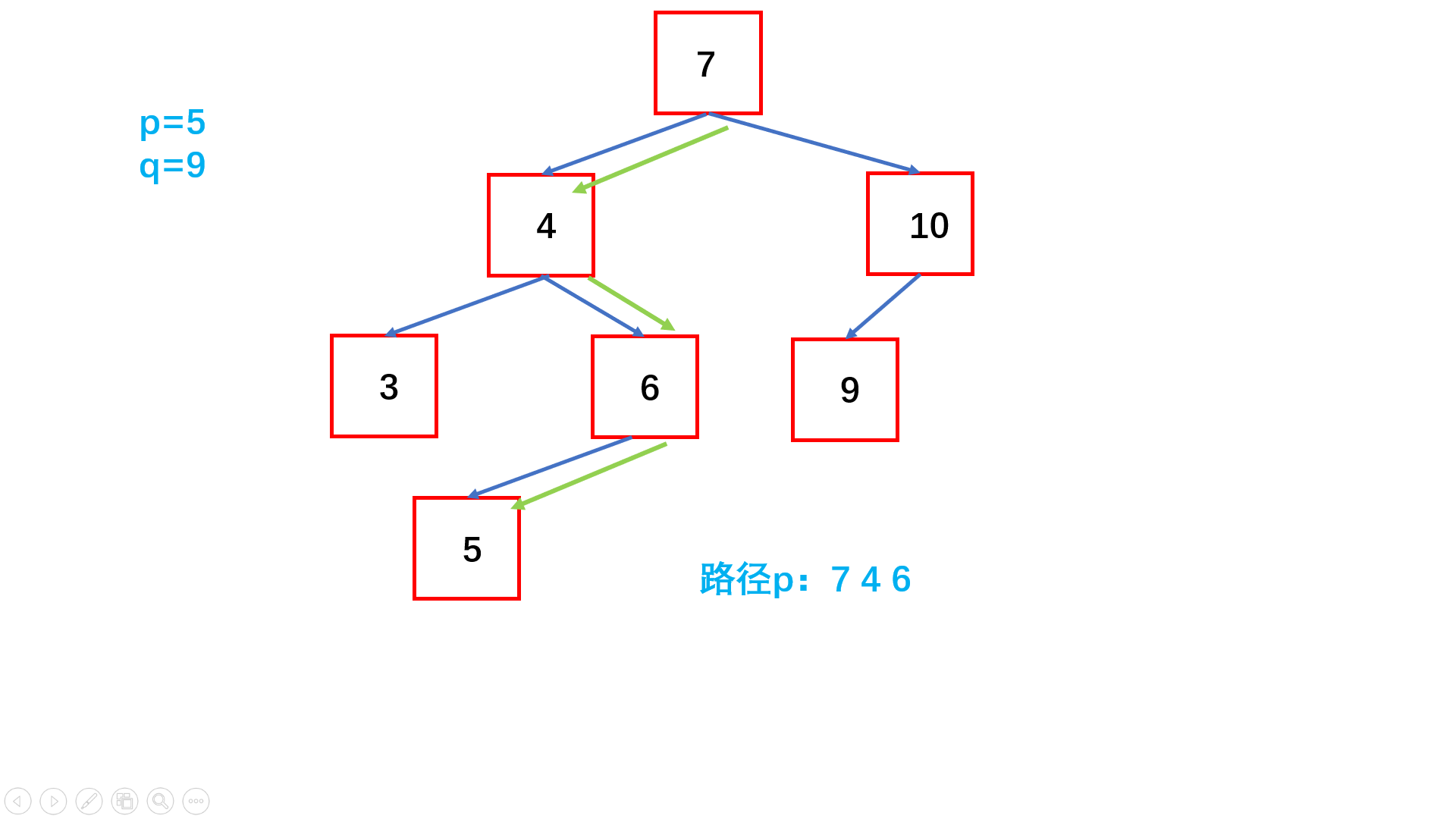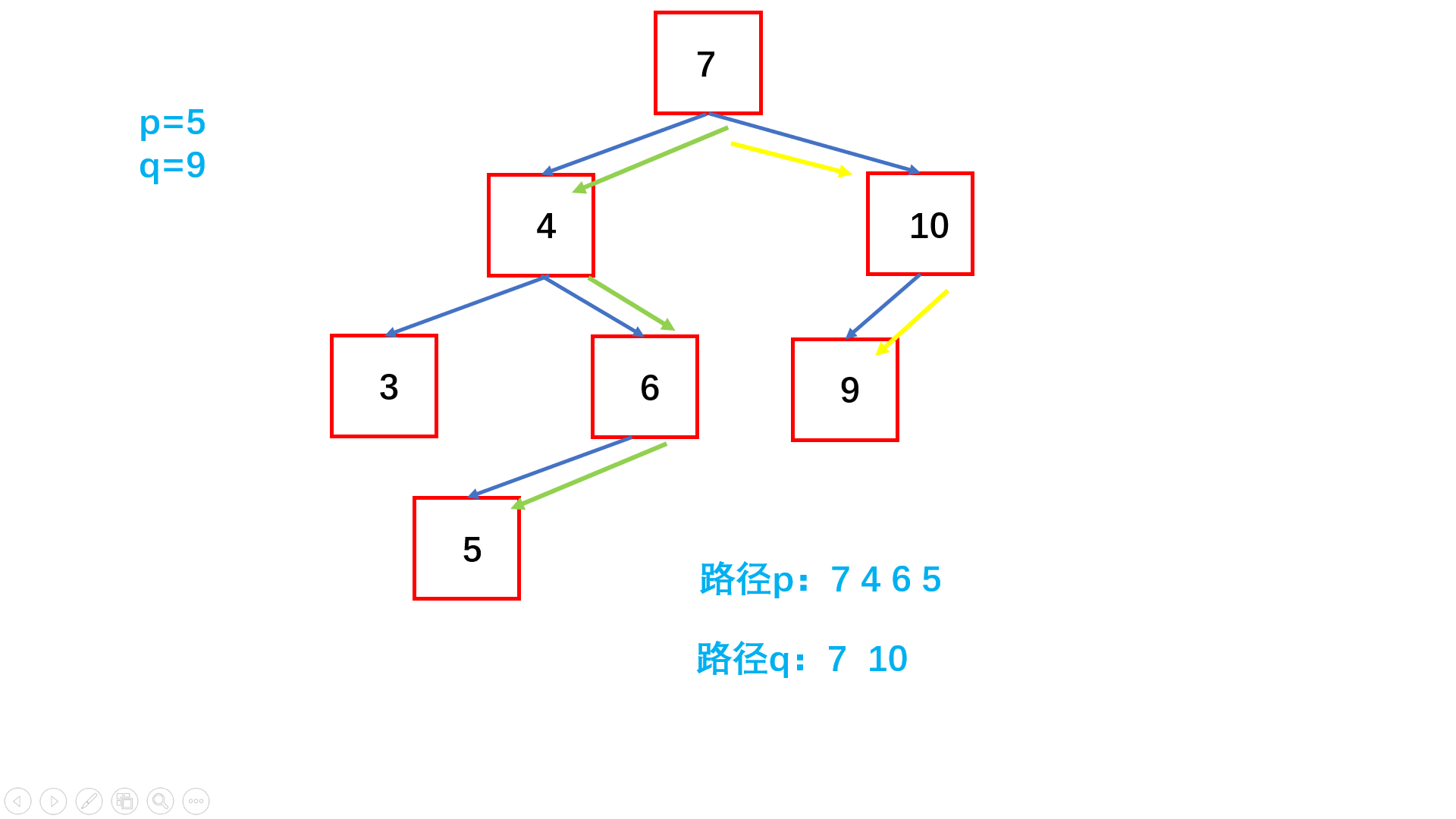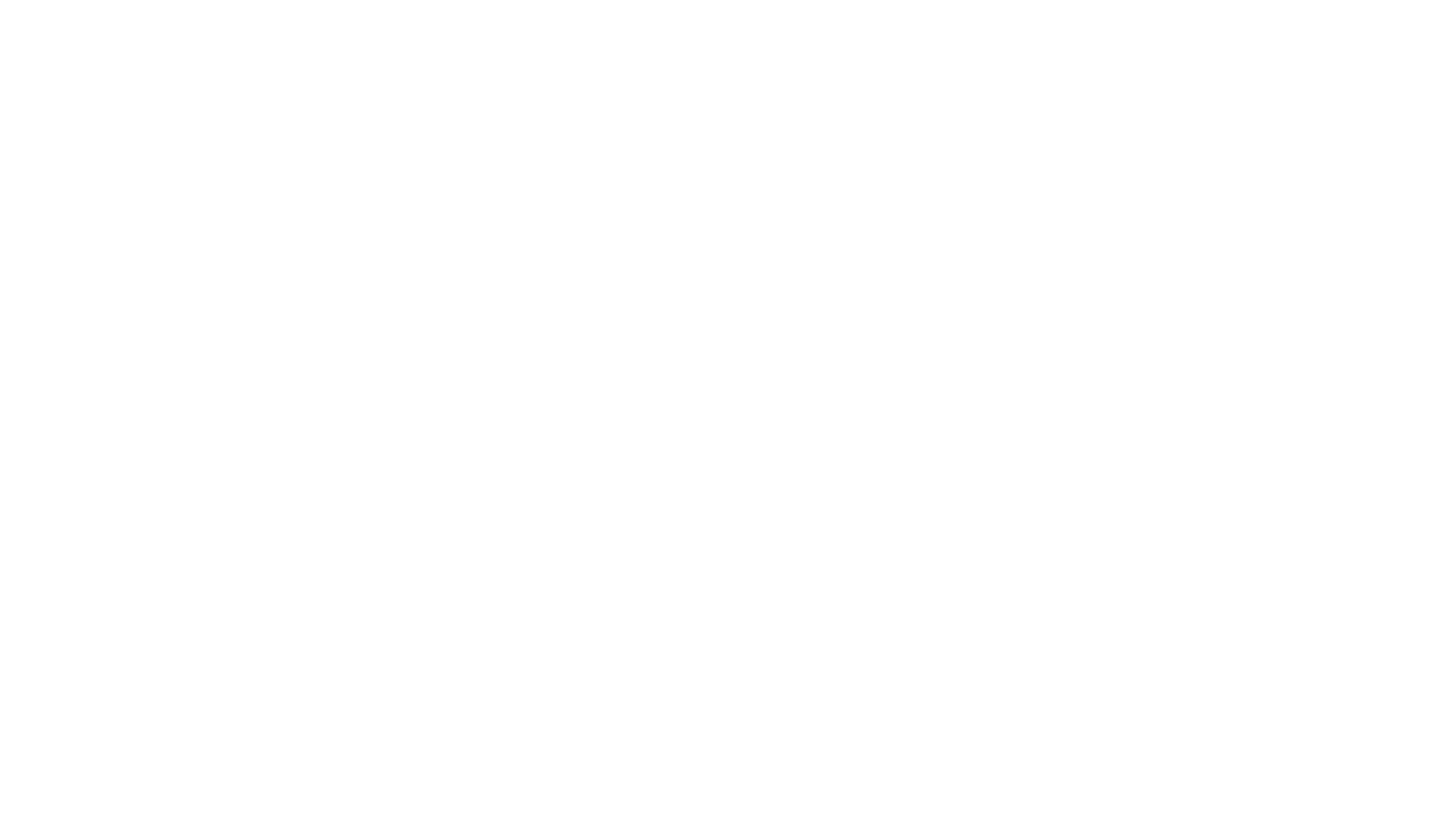
The nearest common ancestor of a binary search tree

Topic link

\

// Method 1 : recursive !
public int lowestCommonAncestor (TreeNode root, int p, int q) {
    
            // write code here
            // Using the characteristics of binary search tree , The left subtree is smaller than the root , Root less than right subtree !
            // To locate the common ancestor node !
            if(root==null) return -1;
            //pq On both sides of the node , therefore  root Is the public node !
            if(root.val>=p&&root.val<=q||root.val<=p&&root.val>=q) return root.val;
            //pq Are on the left side of this node , The description is in the left subtree 
            if(root.val>=q&&root.val>=p)
                return lowestCommonAncestor(root.left,p,q);
            else{
    
                return lowestCommonAncestor(root.right,p,q);
            }
}

• Time complexity O(N) In the worst case, recursively traverse all nodes !
• Spatial complexity O(N), The worst recursion depth is O(N)

• Save the path values of two nodes through two array collections
• Find the last equal node , The common ancestor !

// 
public ArrayList<Integer> getPath(TreeNode root,int x){
    
        ArrayList<Integer> path = new ArrayList<>();
        if(root==null) return path;
        while(root.val!=x){
    // Node values are different , Description has not traversed to  x!
            path.add(root.val);
            // You can't use two if Judge , Because the judgment here will change once ,root The direction of !!!
            if(root.val>x){
    
                // The description is in the left subtree !
                root = root.left;
            }else{
    
                // Description in the right subtree !
                root = root.right;
            }
        }
       // take  x  Node save !
       path.add(x);
        return path;
    }
    public int lowestCommonAncestor (TreeNode root, int p, int q) {
    
        // write code here
        ArrayList<Integer> path1 = getPath(root,p);
        ArrayList<Integer> path2 = getPath(root,q);
        int ret = 0;
        for(int i = 0;i<path1.size()&&i<path2.size();i++){
    
            // there  path1.get(i) Equality cannot be directly compared , Packaging needs to pass equals Compare !
            if(path1.get(i).equals(path2.get(i))){
    
                ret = path2.get(i);// Update the same value 
            }else{
    
                break;// No same value , Exit loop !
            }
        }
        return ret;
    }

Be careful :

Integer Packaging comparison cannot be performed directly through == Compare , To use equals Compare !

• Time complexity : O(N) The worst , After traversing all nodes , That is, a single branch of a binary tree , It becomes a linked list , So you need to compare all nodes !
• Spatial complexity :O(N) The worst , All nodes are recorded and saved !

Find the nearest common ancestor of two nodes in the binary tree

Topic link

describe :

• This is different from the search binary tree above , We can not directly use the characteristics of search binary tree , Find the path directly !

• Here we are just ordinary binary trees , You need to traverse all the nodes , Then find the path !

• And we know that finding a path is the ancestor who found his path , That is, save the parent node relationship of each node !

• We use Map Key value pair save ,key Save the current node ,value Save the root node !

• Here we can traverse to with the help of the queue o1 and o2 The node is OK !

// Method 1 :BFS  breadth-first !
public int lowestCommonAncestor (TreeNode root, int o1, int o2) {
    
        // write code here
        // Save with a data structure o1 and o2 The path of !
        // We know that the binary tree here is just an ordinary binary tree , It's not a binary search 
        // Therefore, you cannot directly locate the node path 
        // Our path cannot be all the parent nodes of this node , Then we can change our thinking !
        // adopt map Record o1 and o2 Parent of node , as well as o1 and o2 A series of ancestors , adopt map The key value pair mapping is saved !
        // And then we're finding out o1 The path of !
        // And then in o1 Find... In the path o2 perhaps o2 The nearest ancestor of is the nearest common ancestor !
        if(root==null) return -1;
        Map<Integer,Integer> map = new HashMap<>();//key Save the current node ,value Save parent !
        map.put(root.val,Integer.MAX_VALUE);// The root node has no parent node !
        // Through the queue , Sequence traversal , When traversal to o1 and o2 The node exits !
        Queue<TreeNode> q = new LinkedList<>();
        q.offer(root);
        while(!map.containsKey(o1)||!map.containsKey(o2)){
    
            TreeNode cur = q.poll();
            if(cur.left!=null){
    
                 // Save the parent-child relationship of the current node !
                map.put(cur.left.val,cur.val);
                q.offer(cur.left);
            }
            if(cur.right!=null){
    
                map.put(cur.right.val,cur.val);
                q.offer(cur.right);
            }
        }
        // take o1 And its ancestral path is preserved !
        Set<Integer> ancestors = new HashSet<>();
        while(map.containsKey(o1)){
    
            ancestors.add(o1);
            // Find his father , All the way to the root node !
            o1 = map.get(o1);
        }
        while(!ancestors.contains(o2)){
    
            // stay o1 Found in ancestors o2 perhaps o2 Our closest ancestors 
            o2 = map.get(o2);
        }
        return o2;
    }

Time complexity :O(N) At worst, all nodes will be traversed recursively !
Spatial complexity :O(N)map and queue The worst O(N)

---

We can do it recursively !

• o1 ,o2 They are located in root On the left and right subtrees of

• o1==root,o2 On its subtree !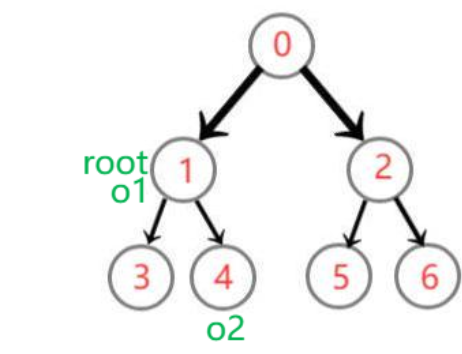

  

  • o2==root,o2 In its subtree

  

// Method 2 : recursive 
 public int lowestCommonAncestor (TreeNode root, int o1, int o2) {
    
        // write code here
        if(root == null) return -1;
        // Find the nearest public node !
        return help(root,o1,o2).val;
    }
    public TreeNode help(TreeNode root,int o1,int o2){
    
        if(root==null||root.val==o1||root.val==o2){
    
            // Recursion to null || eureka o1 perhaps o2
            return root;
        }
        // See if the left subtree exists o1 perhaps o2 node 
        TreeNode left = help(root.left,o1,o2);
        TreeNode right = help(root.right,o1,o2);
        if(left==null){
    
            // The left subtree is empty , explain o1 and o2 The node is in the right subtree !
            return right;
        }
        if(right==null){
    
            return left;
        }
        // explain o1 and o2 On both sides !
        return root;
    }

Time complexity :O(N) At worst, all nodes will be traversed recursively !
Spatial complexity :O(N) Single branch tree , Degenerated into a linked list !