【C語言】深度剖析數據在內存中的存儲

---

前言

Hello這裏是 超人不會飛ke，這麼炎熱的天，最適合呆在空調房裏學習了，小編這幾天也是一直沉迷於學習！那麼今天想給大家總結一下近幾天學習的一些成果，以及分享一些自己的心得體會

本文圍繞數據在內存中的存儲展開討論，運用C語言深度剖析數據在內存中究竟是如何存儲的，並舉一些例題來幫助大家理解和掌握。下面就讓我帶領大家一起走進計算機的內存大門，修煉我們的“內功心法”吧！！

---

1️⃣ 數據類型介紹

 在C語言中，為了錶示生活中各種不同的事物，定義了很多種類型。不僅有我們熟悉的內置類型，還有可以讓我們自己發揮的構造類型。不同的類型在內存中的存儲也是不同的，這裏所指的不同主要是指所占空間大小的不同，當然有時候也可能不同類型看問題的視角不同。
綜上所述，我們可以得出c語言中類型的意義：

1. 規定了不同類型使用時在內存中開辟的空間（所占空間大小）
2. 如何看待內存空間的視角

下面讓我們來整理歸類一下c語言類型吧！

1.整型家族

char（字符類型）
signed char
unsigned char
所占空間大小：1字節
為什麼字符類型也被納入整型家族呢？
因為字符的本質是ASCII碼值，這些值是整型，所以其被納入整型家族

---

short （短整型）
signed short [int]
unsigned short [int]
所占空間大小：2字節

---

int
signed int
unsigned int
所占空間大小：4字節

---

long（長整形）
signed long [int]
unsigned long [int]

在c99標准下還增加了long long長長整型類型，它的大小是八個字節

在這裏我們需要注意兩點：

1. unsigned為無符號類型（為了定義生活中那些沒有負數的數據，c語言定義了帶有unsigned的類型，如：身高、體重）；
2. 當我們創建一個類型為short、int、long的變量時，編譯器會默認其為有符號的變量（如int則默認為signed int）；
3. 而當我們創建一個類型為char的變量時，編譯器不一定會默認其為signed char。不同編譯器對其的默認不同。
4. 在我們創建變量時，如果想要錶示一個只有正數的數可以創建一個unsigned類型，反之可以創建一個signed類型。

2.浮點數家族

float(精度較低)

---

double(精度較高)

浮點數一般用於錶示小數

3.構造類型

數組類型
結構體類型：struct
枚舉類型：enum
聯合類型：union

4.指針類型

int* pi
char* pc
float* pf
double* pd
void* pv
…

---

2️⃣數據在內存中的存儲

那麼知道了數據的類型後，接下來讓我們來探究一下數據在內存中是如何存儲的吧！

我們知道，變量的創建是要在內存中開辟空間的，空間的大小由變量的類型决定。那麼，在開辟的這塊空間中，數據又是以什麼形式存儲進去的呢？不同類型的數據的存儲方式又有什麼不同呢？下面我們將圍繞整型數據和浮點型數據的兩種內存存儲方式展開討論。

---

1. 整型在內存中的存儲

原碼、反碼、補碼

整型在內存中是如何存儲的？
為了探究其真相，我們必須先了解下面的概念——
原碼、反碼、補碼：
計算機中的整數有三種2進制錶示方法，即原碼、反碼和補碼。三種錶示方法均有符號比特和數值比特兩部分，符號比特就是二進制序列的第一比特，用0錶示“正”，用1錶示“負”，而數值比特，正數的原、反、補碼都相同，負整數的三種錶示方法各不相同（負整數的原反補碼錶示方法 具體如下：

1. 原碼：直接將數值按照正負數的形式翻譯成二進制就可以得到原碼；
2. 反碼：原碼除符號比特外按比特取反，得到反碼；
3. 補碼：反碼+1得到補碼。

---

舉個栗子：整型int類型 -6的原碼、反碼、補碼形式如下：

其實，對於整型來說：數據存放內存中其實存放的是補碼。例如上面的-6，如果我們創建了一個int類型的變量int a = -6，那麼其會根據變量的類型在內存中開辟相應大小的空間（這裏變量類型為int則開辟四個字節的空間）。然後再將初始化的數據的補碼存入這塊空間中。不僅是初始化，在對變量進行賦值時也是一樣的道理，只是省去了開辟空間的環節。

如圖所示

內存中的地址單元是一個字節，根據類型開辟對應的空間，防止了空間的浪費。我們知道，一個字節是8個比特比特，因此每個字節中存入了對應數據的8個比特比特，剛好存入了32比特。這裏要注意的是，局部變量的創建是在內存中的棧區中創建的，而全局變量、靜態變量則是在靜態區創建的。

為了方便後續分析，我們將二進制序列轉換為十六進制，如圖（一個十六進制比特對應四個二進制比特）：

那麼問題來了，為什麼整型數據存儲時存放在內存中的是補碼呢？

在計算機系統中，數值一律用補碼來錶示和存儲。原因在於

1. 使用補碼，可以將符號比特和數值域統一處理
2. 同時，加法和减法也可以統一處理（CPU只有加法器）
3. 此外，補碼與原碼相互轉換，其運算過程是相同的，不需要額外的硬件電路。

解釋

1. 用符號比特錶示數據的正負，可以很好地將符號比特和有效比特統一進行處理；
2. CPU只有加法器，那麼對於减法是如何實現的呢？例如計算1-1，則CPU在計算時則轉換為1+(-1)。而對於1+(-1)，如果直接用原碼計算，則：
   1+(-1)=00000000000000000000000000000001+10000000000000000000000000000001=10000000000000000000000000000010
   該結果不等於0，我們並不能得到我們想要的結果。而如果用補碼計算，則：
   1+(-1)=00000000000000000000000000000001+11111111111111111111111111111111=100000000000000000000000000000000
   而這裏進了一比特變為33比特，溢出了int的空間範圍。因此舍弃掉最高比特得到結果為0，是我們想要的結果。由此體現出了使用補碼存儲數據的優越性
3. 這裏也是運用補碼的巧妙之處。補碼原碼相互轉換的過程是相同的，都是取反加1。
   以-1為例
   
   如圖，驗證了補碼與原碼相互轉換運算過程是相同的。

---

大小端的介紹

這裏我們再來討論一個問題。看圖！

上面我們在畫數據存儲進內存空間的圖解的時候，習慣性地將其按順序地存放，那麼，數據在內存中存放的順序是怎麼樣的呢？到底是不是按照我們所畫出地這個順序存放的呢？
這裏我們要了解一個概念——大小端，了解了大小端，便能領悟其中的奧秘。

• 大小端是什麼？

大小端就是c語言中內存存放數據的兩種模式：

• 大端（存儲）模式，是指數據的低比特保存在內存的高地址中，而數據的高比特保存在內存的低地址中；
• 小端（存儲）模式，是指數據的低比特保存在內存的低地址中，而數據的高比特,保存在內存的高地址中。

這裏的比特，是以字節為單比特的，既低字節和高字節組成的字節序，稱為大小端字節序。

• 為什麼會有大小端？

在c語言中存在許多的類型，如short、int、long…它們的大小都各不相同，比如short的大小是2個字節，int的大小是4個字節。多個字節在內存中存放就必然涉及到順序問題，由於可以有很多種不同的排序方法，c語言便保留了兩種：大端模式和小端模式。計算機上的存儲模式可能是大端也可能是小端，具體是哪一個由硬件决定。

這裏我們舉十六進制序列11223344在內存中的存儲為例，畫圖助解：


可以看到，兩種存儲模式是截然相反的。大端存儲更符合人類思考的邏輯，而小端存儲更符號計算機的運行邏輯。

為了加深對大小端的理解，下面我們看一道有關大小端的例題：

設計一個小程序來判斷當前機器的字節序

直接上代碼

#include <stdio.h>
int check_key()
{
    
	int a = 1;//創建變量a
	char* p = (char*)&a;
	//取a的地址（由指針的知識可知，整型變量a的地址是其四個字節空間中最低字節的地址）
	//並强制類型轉換為char*類型，存入指針變量p中
	return *p;//返回p中的值，如果是1則為小端，是0則為大端
}
int main()
{
    
	int ret = check_key();//通過函數的返回值判斷大小端
	if (ret == 1)
	{
    
		printf("小端\n");
	}
	else
	{
    
		printf("大端\n");
	}
	return 0;
}

通過調試觀察內存可以看到（這裏的字節序是用十六進制錶示的），a中的數據確實以小端模式存儲。所以當我們通過改變指針類型為char*訪問其第一個字節中的數據時，得到的是1的最低字節01。如果是大端存儲我們將得到00。

---

整型提昇、算術轉換及例題

掌握了數據在內存中的存儲，我們知道了數據如何往內存中“放”。那麼，有“放”肯定會有“拿”，當我們想要提取並使用內存中的整型數據時，又有什麼奇妙之處呢？想要了解這裏面的奧妙，我們需要掌握這些概念：整型提昇、算術轉換

1.整型提昇

• 什麼是整型提昇？

C的整型算術運算總是至少以缺省整型類型的精度來進行的。為了獲得這個精度，錶達式中的字符和短整型操作數在使用之前被轉換為普通整型，這種轉換稱為整型提昇。

• 整型提昇的意義？

錶達式的整型運算要在CPU的相應運算器件內執行，CPU內整型運算器(ALU)的操作數的字節長度一般就是int的字節長度，同時也是CPU的通用寄存器的長度。因此，即使兩個char類型的相加，在CPU執行時實際上也要先轉換為CPU內整型操作數的標准長度。通用CPU（general-purpose CPU）是難以直接實現兩個8比特字節直接相加運算（雖然機器指令中可能有這種字節相加指令）。所以，錶達式中各種長度可能小於int長度的整型值，都必須先轉換為int或unsigned int，然後才能送入CPU去執行運算。

• 什麼時候會發生整型提昇？

1. char、short類型的操作數在進行錶達式運算之前會先發生整型提昇
2. 在printf函數中，當char、short類型的數據以%d或%u的格式打印 時，會先發生整型提昇（以%u格式打印時轉換為unsigned int)

• 如何進行整型提昇？

*負數的整形提昇：char c1 = -1; 變量c1的二進制比特(補碼)中只有8個比特比特：1111111 ，因為 char 為有符號的 char， 所以整型提昇時，高比特補充符號比特，即為1，提昇之後的結果是 ：
11111111111111111111111111111111
*正數的整形提昇：char c2 = 1; 變量c2的二進制比特(補碼)中只有8個比特比特： 00000001 ，因為 char 為有符號的char，所以整型提昇時，高比特補充符號比特，即為0，提昇之後的結果是 ：
00000000000000000000000000000001

*無符號整形提昇： 高比特補0

舉兩個栗子

例一：

#include <stdio.h>
int main()
{
    
	char a = 1;
	char b = -1;
	char c = a + b;
	//00000001 -> 00000000000000000000000000000001 a
	//11111111 -> 11111111111111111111111111111111 b
	//a+b == 00000000000000000000000000000000
	//00000000 -> c
	return 0;
}

a和b的值被提昇為普通整型，再進行運算。運算後得到的結果也為普通整型，普通整型存入c中，需要發生截斷後再存入，既存入c的值為0
截斷：將占字節大的數據類型賦給占字節小的數據類型時，由於小數據類型空間不足，容納不下大數據類型，因此會發生截斷。截斷的規則是：取大數據類型的低比特存入小數據類型中。（如這裏的int賦給char，既取int的低8比特賦給char）


例二：

#include <stdio.h>
int main()
{
    
	char a = 0xb6;
	short b = 0xb600; 
	int c = 0xb6000000; 
	//
	if (a == 0xb6)
		printf("a"); 
	if (b == 0xb600)
		printf("b"); 
	if (c == 0xb6000000)
		printf("c"); 
	return 0;
}

當變量作為關系操作符、邏輯操作符的操作數時，也是一種錶達式運算，也可能會發生整型提昇。
這裏a,b要進行整形提昇,但是c不需要整形提昇 a,b整形提昇之後,變成了負數,所以錶達式 a==0xb6 , b==0xb600結果是假，返回值是0，但是c不發生整形提昇,則錶達式 c==0xb6000000 的結果是真.
所程序輸出的結果是: c

---

2.算術轉換

如果某個操作符的各個操作數屬於不同的類型，那麼除非其中一個操作數的轉換為另一個操作數的類型，否則操作就無法進行。下面的層次體系稱為尋常算術轉換。

如果某個操作數的類型在上面這個列錶中排名較低（箭頭指向由低到高），那麼首先要轉換為另外一個操作數的類型後執行運算。

舉個栗子

#include <stdio.h>
int main()
{
    
	int a = -4;
	unsigned int b = 8;
	printf("%d", a + b);
	return 0;
}

圖解如下：

注意 算術轉換要合理，否則可能會導致精度丟失

float f = 3.14;
int num = f;//隱式轉換，會有精度丟失

---

3.例題

掌握了整型提昇和算術轉換這兩個“內功”之後，下面讓我們練練幾道題鞏固一下吧


一、

// 輸 出 什 麼 ？ 
#include <stdio.h> 
int main()
{
    
	char a = -1;
	signed char b = -1;
	unsigned char c = -1;
	printf("a=%d,b=%d,c=%d", a, b, c);
	return 0;
}

運行結果




二、

// 輸 出 什 麼 ？ 
#include <stdio.h> 
int main()
{
    
	char a = -128;
	printf("%u\n", a);
	return 0;
}

運行結果




三、

// 輸 出 什 麼 ？ 
#include <stdio.h> 
int main()
{
    
	char a = 128;
	printf("%u\n", a);
	return 0;
}

運行結果

結果與第二題相同




四、

//輸出什麼？
#include <stdio.h> 
int main()
{
    
	int i = -20;
	unsigned int j = 10;
	printf("%d\n", i + j);
}

運行結果




五、

#include <stdio.h>
//結果是什麼?
int main()
{
    
	unsigned int i;
	for (i = 9; i >= 0; i--) 
	{
    
		printf("%u\n", i);
	}
}

因為變量i的類型是unsigned int，所以它不可能小於0，也就是說循環不可能結束。因此該程序將會進入死循環。

六、

//輸出結果為?
#include <stdio.h>
int main()
{
    
	char a[1000];
	int i;
	for (i = 0; i < 1000; i++)
	{
    
		a[i] = -1 - i;
	}
	printf("%d", strlen(a));
	return 0;
}

要弄懂這道題，首先要知道char類型數據的大小範圍。下面畫圖助解：

我們知道，char類型占1個字節，既8個比特比特，8個比特比特可以錶示的數字有2^8也就是256個。如圖從0開始，順時針繞一圈為char能錶示的所有數字。這裏面有一個特例，10000000這個補碼如果轉換為原碼，則為100000000，多了一比特，溢出了char的空間。因此，c語言規定在char類型中，10000000錶示-128。綜上所述，char類型數據的大小範圍是 -128~127。

掌握了這個知識點我們再來看這道題：

運行結果

想要知道其他整型類型的大小範圍，可以通過查詢limits.h頭文件，進行更多的了解。需要我們記住的是char的好兄弟 unsigned char，他的範圍是0~255。

以下是該頭文件中的代碼

#pragma once
#define _INC_LIMITS

#include <vcruntime.h>

#pragma warning(push)
#pragma warning(disable: _VCRUNTIME_DISABLED_WARNINGS)

_CRT_BEGIN_C_HEADER

#define CHAR_BIT 8
#define SCHAR_MIN (-128)
#define SCHAR_MAX 127
#define UCHAR_MAX 0xff

#ifndef _CHAR_UNSIGNED
    #define CHAR_MIN SCHAR_MIN
    #define CHAR_MAX SCHAR_MAX
#else
    #define CHAR_MIN 0
    #define CHAR_MAX UCHAR_MAX
#endif

#define MB_LEN_MAX 5
#define SHRT_MIN (-32768)
#define SHRT_MAX 32767
#define USHRT_MAX 0xffff
#define INT_MIN (-2147483647 - 1)
#define INT_MAX 2147483647
#define UINT_MAX 0xffffffff
#define LONG_MIN (-2147483647L - 1)
#define LONG_MAX 2147483647L
#define ULONG_MAX 0xffffffffUL
#define LLONG_MAX 9223372036854775807i64
#define LLONG_MIN (-9223372036854775807i64 - 1)
#define ULLONG_MAX 0xffffffffffffffffui64

#define _I8_MIN (-127i8 - 1)
#define _I8_MAX 127i8
#define _UI8_MAX 0xffui8

#define _I16_MIN (-32767i16 - 1)
#define _I16_MAX 32767i16
#define _UI16_MAX 0xffffui16

#define _I32_MIN (-2147483647i32 - 1)
#define _I32_MAX 2147483647i32
#define _UI32_MAX 0xffffffffui32

#define _I64_MIN (-9223372036854775807i64 - 1)
#define _I64_MAX 9223372036854775807i64
#define _UI64_MAX 0xffffffffffffffffui64

#ifndef SIZE_MAX
    // SIZE_MAX definition must match exactly with stdint.h for modules support.
    #ifdef _WIN64
        #define SIZE_MAX 0xffffffffffffffffui64
    #else
        #define SIZE_MAX 0xffffffffui32
    #endif
#endif

#if __STDC_WANT_SECURE_LIB__
    #ifndef RSIZE_MAX
        #define RSIZE_MAX (SIZE_MAX >> 1)
    #endif
#endif

_CRT_END_C_HEADER

#pragma warning(pop) // _VCRUNTIME_DISABLED_WARNINGS

---

2. 浮點型在內存中的存儲

我們已經掌握了整型數據在內存中的存儲。而在c語言中，還有另外一個家族——浮點數家族，它們的存儲方式和整型數據的存儲方式一樣嗎？如果不一樣又是怎麼的一種模式呢？下面我們就這幾個問題展開討論。

浮點數，既小數，用於錶示我們生活中的各種小數。常見的浮點數有3.14159，1E10。浮點數家族包括：float, double, long double。

下面我們用一個例子來引入浮點數在內存中的存儲：

#include <stdio.h>
int main()
{
    
	int n = 9;
	float* pFloat = (float*)&n;
	printf("n的值為：%d\n", n);
	printf("*pFloat的值為：%f\n", *pFloat);
	//
	*pFloat = 9.0;
	printf("n的值為：%d\n", n);
	printf("*pFloat的值為：%f\n", *pFloat);
	return 0;
}

輸出的結果：

從該例子中我們可以得出結論：整型數據和浮點數數據在內存中的存儲和提取是不相同的，那麼到底是哪裏不相同呢？為了探究其中的奧妙，我們必須弄清浮點數在內存中的存儲規則：

浮點數在計算機內部的錶示方法
詳細解讀：
根據國際標准IEEE（電氣和電子工程協會） 754，任意一個二進制浮點數V可以錶示成下面的形式： (-1)^S * M * 2^E

(-1)^S 錶示符號比特，當S=0，V為正數；當S=1，V為負數。
M 錶示有效數字（1≤M<2）
2^E 錶示指數比特。

舉個例子 比如十進制的5.0，其二進制錶示為101.0，相當於1.01*2^2
那麼根據上述V的錶示形式，這裏S=0，M=1.01，E=2
比如十進制的5.0，其二進制錶示為-101.0，相當於(-1)^1*1.01*2^2
那麼根據上述V的錶示形式，這裏S=1，M=1.01，E=2

IEEE754規定用S, E, M三個數字錶示任意一個二進制浮點數，又利用這三個數字，規定了浮點數在內存中的存儲模式：

對於32比特的浮點數，最高的1比特是符號比特s，接著的8比特是指數E，剩下的23比特為有效數字M

對於64比特的浮點數，最高的1比特是符號比特s，接著的11比特是指數E，剩下的52比特為有效數字M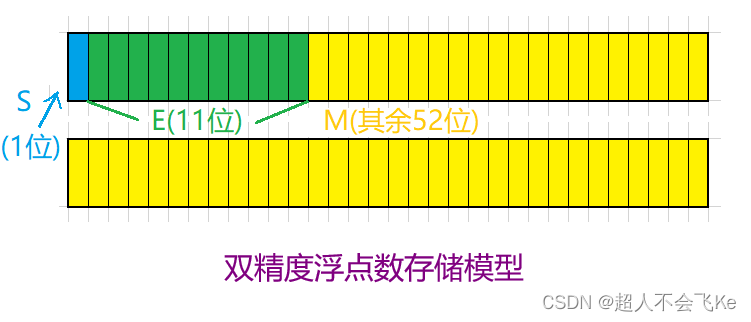

IEEE754對有效數字M和指數E，還有一些特別規定
對於M

前面說過， 1≤M<2 ，也就是說，M可以寫成1.xxxxxx的形式，其中xxxxxx錶示小數部分。IEEE754規定，在計算機內部保存M時，默認這個數的第一比特總是1，因此可以被舍去，只保存後面的xxxxxx部分。比如保存1.01的時候，只保存01，等到讀取的時候，再把第一比特的1加上去。這樣做的目的，是節省1比特有效數字。以32比特浮點數為例，留給M只有23比特，將第一比特的1舍去以後，相當於可以保存24比特有效數字。
（注：在存儲浮點數時，如果M的舍去第一比特1後，後面的xxxxxx部分不足23比特（或64比特），則在後面補0到比特數够了為止）
對於指數E

首先，E為一個無符號整數（unsigned int） 這意味著，如果E為8比特，它的取值範圍為0~255；如果E為11比特，它的取值範圍為0~2047。但是，我們知道，科學計數法中的E是可以出現負數的，所以IEEE754規定，存入內存時E的真實值必須再加上一個中間數，對於8比特的E，這個中間數是127；對於11比特的E，這個中間數是1023。 比如，2^10的E是10，所以保存成32比特浮點數時，必須保存成10+127=137，即10001001。

---

而當我們從內存中提取出浮點數時，E還可以分為三種情况。


1.E不全為0或不全為1

此時按正常的規則進行取出其浮點數，既指數E减去127（或1023）得到E真實值，再將有效數字M前面補上第一比特的1得到真實的M。
比如：
二進制序列0 01111110 00000000000000000000000
可以觀察到這個二進制序列有32比特，是一個單精度浮點數。
第一步：讀取第一比特S為0，則該數的浮點數為正數。
第二步：讀第一比特的後八比特，這八比特錶示的數减去127得到E的真實值E = 01111110 - 01111111 = -1
第三步：讀剩餘的23比特，這23比特補上第一比特1得到M，則M = 1.00000000000000000000000
因此該數等於 (-1)^0 * 1.00000000000000000000000 * 2^(-1) = 0.1，轉化為十進制則為0.5


2.E全為0

這時，浮點數的指數E等於1-127（或者1-1023）即為真實值，有效數字M不再加上第一比特的1，而是還原為0.xxxxxx的小數。這樣做是為了錶示±0，以及接近於0的很小的數字。


3.E全為1

這時，如果有效數字M全為0，錶示±無窮大（正負取决於符號比特s）

---

OK！了解了浮點數在內存中的存儲規則，我們再來分析一下開頭引入的例題吧！為什麼這裏會出現意向不到的結果呢？讓我們一步一步仔細分析（分為兩部分分析）：

//引例
#include <stdio.h>
int main()
{
    
    //上半部分
	int n = 9;
	float* pFloat = (float*)&n;
	printf("n的值為：%d\n", n);
	printf("*pFloat的值為：%f\n", *pFloat);
	//下半部分
	*pFloat = 9.0;
	printf("n的值為：%d\n", n);
	printf("*pFloat的值為：%f\n", *pFloat);
	return 0;
}

上半部分：





下半部分

由此我們可以得出結論，打印發生异常的原因是我們存入數據和取出數據的方式不同，得到的結果就可能會出乎我們的意料。我們寫代碼的時候要謹慎小心，和內存“打好交道”，减少bug的出現~

---

總結

今天的分享到這裏就結束啦！如有錯誤，歡迎大佬指正~
這裏想分享一句今天看到的一句話：Do what you love, love what you do.
做自己喜歡的事是生活的意義！加油xdm！
如果看到這裏不妨給個三連噢~