当前位置:网站首页>Foundations of Cryptography
Foundations of Cryptography
2022-06-24 21:13:00 【gaoZhuanMing】
1. Hash
hash : { 0 , 1 } ∗ → { 0 , 1 } k \text{ hash }: \{ 0, 1 \}^* \rightarrow \{ 0, 1 \}^k hash :{ 0,1}∗→{ 0,1}k
Mapping variable length inputs to fixed length outputs .
characteristic :
- Anti collision : Different inputs map to different outputs ;
- Irreversible : The input... Cannot be inferred from the output result ;
- Randomness : Cannot infer output from input ;
Such as :MD5, SHA-1, SHA-256 etc. .
2. digital signature
For tamper proof .
Generate the key :
( s , v ) ← G ( 1 n ) (s, v) \leftarrow \text{G}(1^n) (s,v)←G(1n)
Generate signature private key s s s And verify the public key v v v . Public key verification is generally advertised , Signing the private key requires strict confidentiality .
Private key signature :
σ ← Sig s ( m ) \sigma \leftarrow \text{Sig}_s(m) σ←Sigs(m)
Use the signing private key s s s The clear m m m To sign , Get the output σ \sigma σ .
Public key verification :
b ← Vfy v ( m , σ ) b \leftarrow \text{Vfy}_v(m, \sigma) b←Vfyv(m,σ)
Given plaintext m m m And signature σ \sigma σ , Use authentication public key v v v verification σ \sigma σ Whether it is m m m The signature of the , Output a Boolean value .
Such as :ECDSA etc. .
3. Symmetric encryption
Encryption and decryption use the same key .
Generate the key :
k ← G ( 1 n ) k \leftarrow \text{G}(1^n) k←G(1n)
The key needs to be kept strictly confidential .
encryption :
c ← E k ( m ) c \leftarrow \text{E}_k(m) c←Ek(m)
Use key k k k The clear m m m To encrypt , Get the ciphertext c c c .
Decrypt :
m ← D k ( c ) m \leftarrow \text{D}_k(c) m←Dk(c)
Use key k k k To ciphertext c c c Decrypt to get plaintext m m m .
Such as :DES etc. .
4. Asymmetric encryption
Encryption and decryption use different keys .
Generate the key :
( e , d ) ← G ( 1 n ) (e, d) \leftarrow \text{G}(1^n) (e,d)←G(1n)
Generate encryption public key e e e And decrypt the private key d d d . Encryption public key is generally advertised , Decrypting the private key requires strict confidentiality .
Public key encryption :
c ← E e ( m ) c \leftarrow \text{E}_e(m) c←Ee(m)
Use public key e e e The clear m m m To encrypt , Get the ciphertext c c c .
Private key decryption :
m ← D d ( c ) m \leftarrow \text{D}_d(c) m←Dd(c)
Use private key d d d To ciphertext c c c Decrypt to get plaintext m m m .
Such as :RSA, DAS etc. .
The encryption and decryption speed of asymmetric encryption algorithm is much lower than that of symmetric encryption algorithm , Therefore, it is not applicable to the case with large amount of data .
Because the efficiency of asymmetric encryption is relatively low , But the key of symmetric encryption needs to be kept strictly confidential , Therefore, asymmetric encryption can first be used to transmit the key required for symmetric encryption , Then use symmetric encryption .
5. Use a combination of
encryption & Signature :
c ← E k ( m ) σ ← Sig s ( c ) c \leftarrow \text{E}_k(m) \\ \sigma \leftarrow \text{Sig}_s(c) c←Ek(m)σ←Sigs(c)
Encrypt first , Post signature , Prevent ciphertext from being tampered with .
verification & Decrypt :
Vfy v ( c , σ ) = ? 1 m ← D k ( c ) \text{Vfy}_v(c, \sigma) \overset{?}= 1 \\ m \leftarrow \text{D}_k(c) Vfyv(c,σ)=?1m←Dk(c)
Decryption is required only after verification .
边栏推荐
- 全上链哈希游戏dapp系统定制(方案设计)
- More than ten years' work experience is recommended at the bottom of the box: how much does it cost to find a job? See here! Brothers and sisters are recommended to collect and pay attention
- maptalks:数据归一化处理与分层设色图层加载
- Self signed certificate generation
- After screwing the screws in the factory for two years, I earned more than 10000 yuan a month by "testing" and counterattacked
- Memo mode - game archiving
- Axi DMA IP core operation process
- 浅谈MySql update会锁定哪些范围的数据
- 等保备案是等保测评吗?两者是什么关系?
- Bean lifecycle flowchart
猜你喜欢

Grating diffraction

Agency mode -- Jiangnan leather shoes factory

DHCP operation

Summary of idea practical skills: how to rename a project or module to completely solve all the problems you encounter that do not work. It is suggested that the five-star collection be your daughter

Codeforces Round #720 (Div. 2)

Sleep revolution - find the right length of rest

Memo mode - game archiving
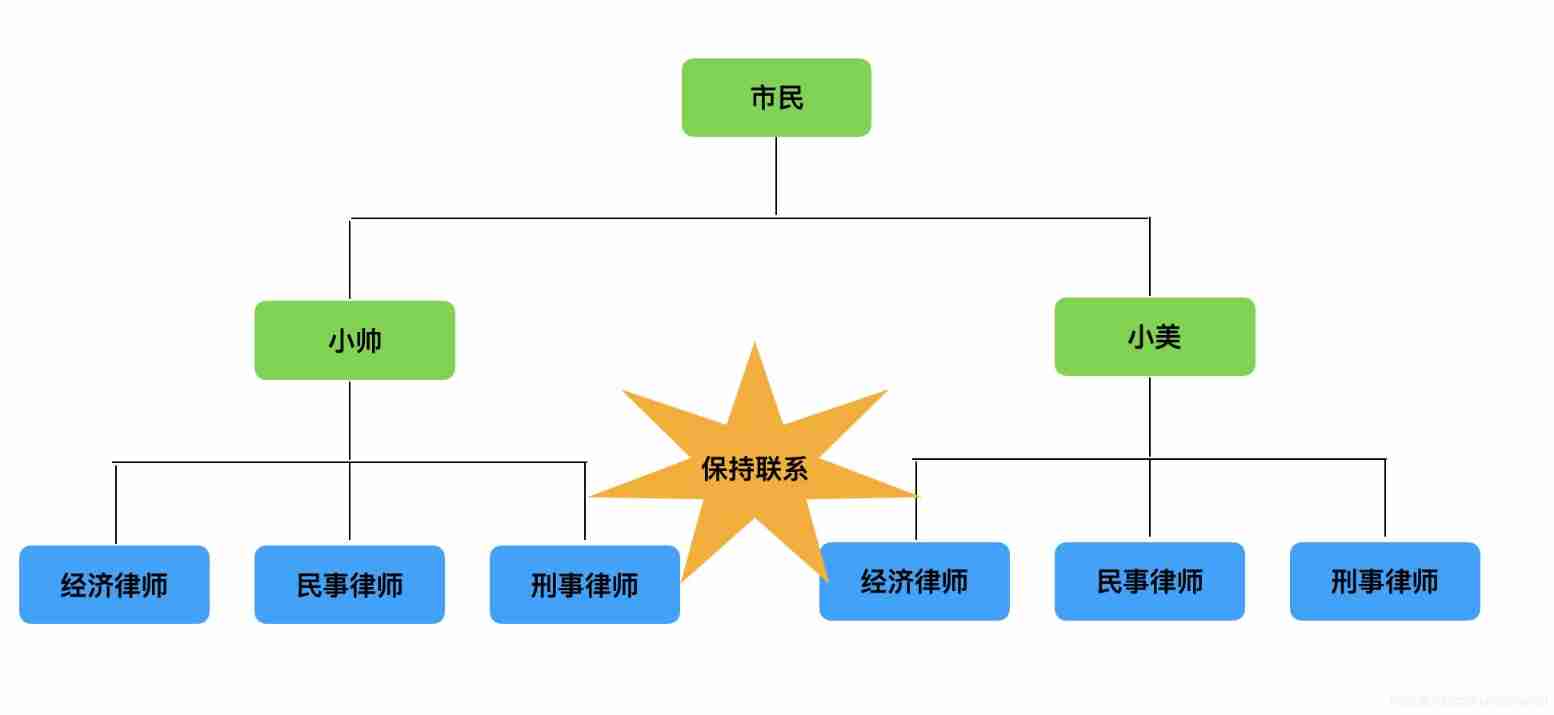
Bridging mode -- law firm

Does the developer want to change to software testing?

The Google File System (GFS) learning notes
随机推荐
Docker deploy mysql5.7
JMeter basic learning records
[multi thread performance tuning] multi thread lock optimization (Part 1): optimization method of synchronized synchronization lock
An example illustrates restful API
What does virtualization mean? What technologies are included? What is the difference with private cloud?
Shrimp skin test surface treated
Bridging mode -- law firm
Leetcode(135)——分发糖果
Learn to use a new technology quickly
The difference between RPC and restful
B站带货当学新东方
Common member methods of the calendar class
database/sql
Reflection - class object function - get method (case)
maptalks:数据归一化处理与分层设色图层加载
Learn together and make progress together. Welcome to exchange
Tool composition in JMeter
Procedural life: a few things you should know when entering the workplace
Curl command
Sleep revolution - find the right length of rest