当前位置:网站首页>4. 寻找两个正序数组的中位数
4. 寻找两个正序数组的中位数
2022-07-23 08:03:00 【ATTACH_Fine】
题目
给定两个大小分别为 m 和 n 的正序(从小到大)数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。
算法的时间复杂度应该为 O(log (m+n)) 。
示例:
思路
根据中位数的定义,当 m+n 是奇数时,中位数是两个有序数组中的第 (m+n)/2 个元素,当 m+n 是偶数时,中位数是两个有序数组中的第 (m+n)/2个元素和第 (m+n)/2+1 个元素的平均值。因此,这道题可以转化成寻找两个有序数组中的第 k 小的数,其中 k 为 (m+n)/2或 (m+n)/2+1。

代码
class Solution {
public double findMedianSortedArrays(int[] nums1, int[] nums2) {
int len1 = nums1.length;
int len2 = nums2.length;
int totalLen = len1 + len2;
//奇数,中位数是两个有序数组中的第 (m+n)/2 个元素
if(totalLen % 2 == 1){
double median = getKthElement(nums1,nums2,totalLen/2+1);
return median;
}else{
//偶数时,中位数是两个有序数组中的第 (m+n)/2个元素和第 (m+n)/2+1 个元素的平均值
double median = (getKthElement(nums1,nums2,totalLen/2) + getKthElement(nums1,nums2,totalLen/2 + 1)) / 2.0;
return median;
}
}
public int getKthElement(int[] nums1,int[] nums2,int k){
int len1 = nums1.length;
int len2 = nums2.length;
int index1 = 0, index2 = 0;
while(true){
if(index1 == len1){
return nums2[index2+k-1];
}
if(index2 == len2){
return nums1[index1+k-1];
}
//我们要找第 1 小的数字,所以只需判断两个数组中第一个数字哪个小就可以了
if(k==1){
return Math.min(nums1[index1],nums2[index2]);
}
int half = k / 2;
//删除" 了一些元素(这些元素都比第 k 小的元素要小)更新index的值
//如果超过数组的长度,就指向数组的末尾
int newIndex1 = Math.min(index1 + half,len1) - 1;
int newIndex2 = Math.min(index2 + half,len2) - 1;
if(nums1[newIndex1] <= nums2[newIndex2]){
k -= (newIndex1-index1+1);
index1 = newIndex1 + 1;
}else{
k -= (newIndex2-index2+1);
index2 = newIndex2 + 1;
}
}
}
}
边栏推荐
- Network security note 1 - Security of Internet Protocol
- SDF refraction and reflection effect recording
- 网络安全笔记1——Internet协议的安全性
- Surrounded Regions
- canvas橡皮擦功能
- ThreadLocal 面试夺命11连问
- Uiscrollview (uicollectionview) prohibits horizontal and vertical sliding at the same time
- 第六天笔记
- NR Modulation 5
- Excitation generator, monitor
猜你喜欢

How about the nuclear display performance of Ruilong R7 Pro 6850h? What level is it equivalent to
鸡与蛋,产品与策略

rtx3080ti和rtx3080差距 3080和3080ti参数对比

How many processors is Tianji 1100 equivalent to snapdragon? How about Tianji 1100 equivalent to snapdragon
Day108.尚医通:医院模拟系统接口对接 - 医院|科室|排班 增删改分页条件查询

Notes du jour 5
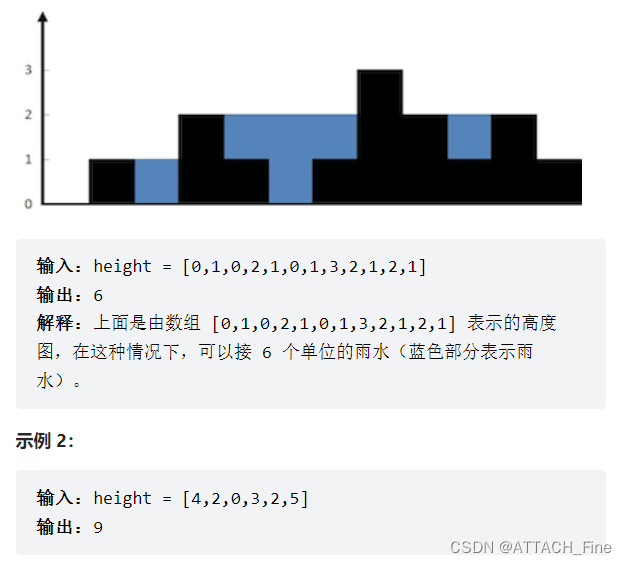
单调栈!!!

Remember that a vulnhub target plane exercise successfully won the root permission

Detailed explanation of knapsack problem

How about Celeron n5095 Processor? What is the equivalent level of Intel n5095 core display
随机推荐
js 实现通过身份证获取年龄
中等靶场
AppScan的安装与使用
FPGA工程师如何进行复杂系统设计?
JS realize random generation of UUID
Day 12 notes
200 lines of code, in-depth analysis of the principle and implementation of dynamic calculation diagram
js 实现随机生成UUID
锐龙R7 PRO 6850H核显性能怎么样?相当于什么水平
The difference between rtx3080ti and 3090. Which one is more cost-effective, rtx3080ti or 3090
STM32输出正弦波+cubeMX配置+HAL库
How about Celeron n5095 Processor? What is the equivalent level of Intel n5095 core display
How about the performance of Ruilong R7 Pro 5875u? What level is it equivalent to
强化學習——策略梯度理解點
STM32 output sine wave +cubemx configuration +hal Library
Fastadmin changes the pop-up size of the default table button
天玑920相当于骁龙什么 天玑920相当于骁龙多少 天玑920怎么样
The difference between Celeron n4000 and Celeron n5095
SDF refraction and reflection effect recording
NOTICE: PHP message: PHP Warning: PHP Startup: Unable to load dynamic library ‘*****‘