当前位置：网站首页>TASK03|概率论

TASK03|概率论

2022-06-25 10:20:00 【speoki】

目录

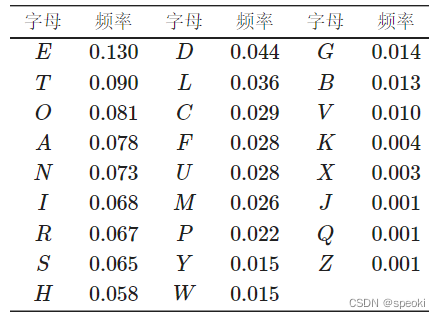
在这里插入图片描述
（1）英文写作中的频率表

随机现象与概率

概率论主要研究能大量重复的随机现象‘

（1）随机试验：可重复的随机现象又称为随机试验
（2）样本点：一切可能发生的基本结果
（3）样本空间：随机现象所有基本结果（样本点）的全体称为这个随机现象的样本空间
（4）随机事件：随机现象的某些基本结果组成的集合称为随机事件
（5）事件间的关系：

  • 包含
  • 相等
  • 互不相容
  • 必然与不可能事件
    （6）事件的运算：
  • 对立
  • 并
  • 交
  • 差
    （7）概率的公理化定义：
  • 非负性公理
  • 正则性公理
  • 可加性公理
    （8）事件的独立性

模拟频率近似概率

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
#提供了和 MATLAB 类似的绘图 API
#调用matplotlib.pyplot的绘图函数plot()进行绘图的时候，或者生成一个figure画布的时候，可以直接在你的python console里面生成图像。
plt.style.use("ggplot")
# 画布风格 使用plt.style.available可以找适合图形的风格
import warnings
warnings.filterwarnings("ignore")
#忽略代码中的红色警告
plt.rcParams['font.sans-serif']=['SimHei','Songti SC','STFangsong']
#定义图形默认属性 设置字体
plt.rcParams['axes.unicode_minus']=False
#用来正常显示负号
import seaborn as sns

import random
def Simulate_coin(test_num):
random_seed(100)#定义随机数种子
coin_list=[1 if random.random()>=0.5]else 0 for i range(test_num)]#模拟试验结果
#大于等于0.5的算1 否则算0
coin_frequence = np.cumsum(coin_list)/（np.arrange(len(coin_list))+1）
#计算正面为1的概率
plt.figure(figsize=(10,6))
#绘图，指定画布的大小
plt.plot(np.arrange(len(coin_list))+1,coin_frequence,c='blue',alpha=0.7)
#横坐标测验的次数，纵坐标频度
plt.xlabel("test_index")
plt.ylabel("frequence")
plt.title(str(test_num)+" times")
plt.show()
Simulate_coin(test_num = 600)
Simulate_coin(test_num = 1000)
Simulate_coin(test_num = 6000)
Simulate_coin(test_num = 10000)

条件概率，乘法公式，全概率公式与贝叶斯公式

（1）条件概率
P ( A ∣ B ) = P ( A B ) P ( B ) P(A \mid B)=\frac{P(A B)}{P(B)} P(A∣B)=P(B)P(AB)​
（2）乘法公式

  • 若 P ( B ) > 0 P(B)>0 P(B)>0, 则 P ( A B ) = P ( B ) P ( A ∣ B ) P(A B)=P(B) P(A \mid B) P(AB)=P(B)P(A∣B)
  • 若 P ( A 1 A 2 ⋯ A n − 1 ) > 0 P\left(A_{1} A_{2} \cdots A_{n-1}\right)>0 P(A1​A2​⋯An−1​)>0, 则 P ( A 1 A 2 ⋯ A n ) = P ( A 1 ) P ( A 2 ∣ A 1 ) P ( A 3 ∣ A 1 A 2 ) ⋯ P ( A n ∣ A 1 A 2 ⋯ A n − 1 ) P\left(A_{1} A_{2} \cdots A_{n}\right)=P\left(A_{1}\right) P\left(A_{2} \mid A_{1}\right) P\left(A_{3} \mid A_{1} A_{2}\right) \cdots P\left(A_{n} \mid A_{1} A_{2} \cdots A_{n-1}\right) P(A1​A2​⋯An​)=P(A1​)P(A2​∣A1​)P(A3​∣A1​A2​)⋯P(An​∣A1​A2​⋯An−1​)

exp:

P ( A ˉ 1 A ˉ 2 A 3 ) = P ( A ˉ 1 ) P\left(\bar{A}_{1} \bar{A}_{2} A_{3}\right)=P\left(\bar{A}_{1}\right) P(Aˉ1​Aˉ2​A3​)=P(Aˉ1​)

P ( A ˉ 2 ∣ A ˉ 1 ) P ( A 3 ∣ A ˉ 1 A ˉ 2 ) = 90 100 ⋅ 89 99 ⋅ 10 98 = 0.0826. P\left(\bar{A}_{2} \mid \bar{A}_{1}\right) P\left(A_{3} \mid \bar{A}_{1} \bar{A}_{2}\right)=\frac{90}{100} \cdot \frac{89}{99} \cdot \frac{10}{98}=0.0826 . P(Aˉ2​∣Aˉ1​)P(A3​∣Aˉ1​Aˉ2​)=10090​⋅9989​⋅9810​=0.0826.

(3)全概率公式
P ( A ) = ∑ i = 1 n P ( A ∣ B i ) P ( B i ) P(A)=\sum_{i=1}^{n} P\left(A \mid B_{i}\right) P\left(B_{i}\right) P(A)=i=1∑n​P(A∣Bi​)P(Bi​)

在这里插入图片描述
（4）贝叶斯公式

用简单的 P ( A ∣ B k ) P\left(A \mid B_{k}\right) P(A∣Bk​)求解复杂的 P ( B k ∣ A ) P\left(B_{k} \mid A\right) P(Bk​∣A)

P ( B k ∣ A ) = P ( A B k ) P ( A ) P\left(B_{k} \mid A\right) = \frac{P(AB_k)}{P(A)} P(Bk​∣A)=P(A)P(ABk​)​

对分子分母分别使用乘法公式和全概率公式展开，即：
P ( B k ∣ A ) = P ( A ∣ B k ) P ( B k ) ∑ i = 1 n P ( A ∣ B i ) P ( B i ) , k = 1 , 2 , ⋯   , n P\left(B_{k} \mid A\right)=\frac{P\left(A \mid B_{k}\right) P\left(B_{k}\right)}{\sum_{i=1}^{n} P\left(A \mid B_{i}\right) P\left(B_{i}\right)}, \quad k=1,2, \cdots, n P(Bk​∣A)=∑i=1n​P(A∣Bi​)P(Bi​)P(A∣Bk​)P(Bk​)​,k=1,2,⋯,n

三门问题

参赛者会看见三扇关闭了的门，其中一扇的后面有一辆汽车，选中后面有车的那扇门就可以赢得该汽车，而另外两扇门后面则各藏有1只山羊。当参赛者选定了一扇门，但未去开启它的时候，节目主持人会开启剩下两扇门的其中一扇，露出其中1只山羊。主持人其后会问参赛者要不要换另一扇仍然关上的门。问题是：换另一扇门会否增加参赛者赢得汽车的机率？
在主持人不打开门时, 选手抽中车的概率为 1 / 3 1 / 3 1/3
P ( A ) = P ( B ) = P ( C ) = 1 / 3 \begin{aligned} &P(A)=P(B)=P(C)=1 / 3\\ \end{aligned} ​P(A)=P(B)=P(C)=1/3​
假设：
A: 选手选择第二扇门，第一扇门是车，
B: 选手选择第二扇门，第二扇门是车，
C: 选手选择第二扇门，第三扇门是车，
D: 主持人打开第一扇门
根据语义我们可以列出概率公式
P ( D ∣ A ) = 0 P ( D ∣ B ) = 1 / 2 P ( D ∣ C ) = 1 \begin{aligned} P(D|A)=0 P(D|B)=1/2 P(D|C)=1 \end{aligned} P(D∣A)=0P(D∣B)=1/2P(D∣C)=1​
根据贝叶斯公式： P ( D ) = P ( A ) P ( D ∣ A ) + P ( B ) P ( D ∣ B ) + P ( C ) P ( D ∣ C ) = 1 / 2 P ( C ∣ D ) = P ( C ) P ( D ∣ C ) / P ( D ) = 2 / 3 P ( B ∣ D ) = P ( B ) P ( D ∣ B ) / P ( D ) = 1 / 3 \begin{aligned} &\text{根据贝叶斯公式：}\\ &P(D)=P(A) P(D \mid A)+P(B) P(D \mid B)+P(C) P(D \mid C)=1 / 2 \\ &P(C \mid D)=P(C) P(D \mid C) / P(D)=2 / 3 \\ &P(B \mid D)=P(B) P(D \mid B) / P(D)=1 / 3 \end{aligned} ​根据贝叶斯公式：P(D)=P(A)P(D∣A)+P(B)P(D∣B)+P(C)P(D∣C)=1/2P(C∣D)=P(C)P(D∣C)/P(D)=2/3P(B∣D)=P(B)P(D∣B)/P(D)=1/3​

import random
class MontyHall:
  def __init__(self,n): #构造函数
	self.n=n#试验的次数
	self.change=0#记录换才能拿到车的次数
	sellf.No_change=0#不换
  def start(self):
	for i in range(self,n):
		door_list=[1,2,3]#三扇门
		challenger_door = random.choice(door_list)
		##随机选择了其中一扇
		car_door=  random.choice(door_list)
		#车的门
		##没有被挑战者选中的剩下的门
		door_list.remove(challenger_door)
		
		if challenger_door==car_door:
			host_door = random.choice(door_list)
			door.remove(host_door)
		#不换才能拿车
			self.No_change+=1
		else:
			self.change+=1
		#换了才能拿车
		  print("换且能拿到车的概率：%.2f " % (self.change/self.n * 100) + "%")
        print("不换也能拿到车的概率：%.2f"% (self.No_change/self.n * 100) + "%")
		
if __name__ == "__main__":
    mh = MontyHall(1000000)
    mh.start()

一维随机变量

随机变量分为离散的和连续的
计算一个由随机变量表示的随机事件的概率的思路有两种：直接计算法（利用分布函数计算） 和 间接计算法（利用密度函数计算）

F ( x ) = P ( X ⩽ x ) F(x)=P(X \leqslant x) F(x)=P(X⩽x)

0 ⩽ F ( x ) ⩽ 1 0 \leqslant F(x) \leqslant 1 0⩽F(x)⩽1

  • F ( − ∞ ) = lim ⁡ x → − ∞ F ( x ) = 0 F(-\infty)=\lim _{x \rightarrow-\infty} F(x)=0 F(−∞)=limx→−∞​F(x)=0 ,这是因为事件“ X ⩽ − ∞ X \leqslant-\infty X⩽−∞ "是不可能事件。
  • F ( + ∞ ) = lim ⁡ x → + ∞ F ( x ) = 1 F(+\infty)=\lim _{x \rightarrow+\infty} F(x)=1 F(+∞)=limx→+∞​F(x)=1, 这是因为事件“ X ⩽ + ∞ X \leqslant+\infty X⩽+∞ "是必然事件。

P ( a < X ⩽ b ) = F ( b ) − F ( a ) P ( X = a ) = F ( a ) − F ( a − 0 ) P ( X ⩾ b ) = 1 − F ( b − 0 ) P ( X > b ) = 1 − F ( b ) P ( X < b ) = F ( b − 0 ) P ( a < X < b ) = F ( b − 0 ) − F ( a ) P ( a ⩽ X ⩽ b ) = F ( b ) − F ( a − 0 ) P ( a ⩽ X < b ) = F ( b − 0 ) − F ( a − 0 ) \begin{aligned} &P(a<X \leqslant b)=F(b)-F(a) \\ &P(X=a)=F(a)-F(a-0) \\ &P(X \geqslant b)=1-F(b-0) \\ &P(X>b)=1-F(b)\\ &P(X<b)=F(b-0) \\ &P(a<X<b)=F(b-0)-F(a) \\ &P(a \leqslant X \leqslant b)=F(b)-F(a-0) \\ &P(a \leqslant X<b)=F(b-0)-F(a-0) \end{aligned} ​P(a<X⩽b)=F(b)−F(a)P(X=a)=F(a)−F(a−0)P(X⩾b)=1−F(b−0)P(X>b)=1−F(b)P(X<b)=F(b−0)P(a<X<b)=F(b−0)−F(a)P(a⩽X⩽b)=F(b)−F(a−0)P(a⩽X<b)=F(b−0)−F(a−0)​

a a a 与 b b b 处连续时, 有
F ( a − 0 ) = F ( a ) , F ( b − 0 ) = F ( b ) F(a-0)=F(a), \quad F(b-0)=F(b) F(a−0)=F(a),F(b−0)=F(b)

利用密度函数计算某个区域内的概率

P ( a ⩽ X ⩽ b ) = ∫ a b p ( x ) d x P(a \leqslant X \leqslant b)=\int_{a}^{b} p(x) d x P(a⩽X⩽b)=∫ab​p(x)dx

离散型 :
分布列

X x 1 x 2 ⋯ x n ⋯ P p ( x 1 ) p ( x 2 ) ⋯ p ( x n ) ⋯ \begin{array}{c|ccccc} X & x_{1} & x_{2} & \cdots & x_{n} & \cdots \\ \hline P & p\left(x_{1}\right) & p\left(x_{2}\right) & \cdots & p\left(x_{n}\right) & \cdots \end{array} XP​x1​p(x1​)​x2​p(x2​)​⋯⋯​xn​p(xn​)​⋯⋯​​

连续型：
exp:
柯西分布的密度函数,对分布函数求导
在这里插入图片描述

## 已知柯西分布的密度函数求分布函数
from sympy import *
x = symbols('x')
p_x = 1/pi*(1/(1+x**2))
integrate(p_x,(x,-∞，x))
#积分 从负无穷到x

在这里插入图片描述

from sympy import *
x = symbols('x')
f_x = 1/pi*(atan(x)+pi/2)
diff(f_x,x,1)
#求导

均匀分布：

密度函数为
U ( a , b ) U(a, b) U(a,b)
p ( x ) = { 1 b − a , a ⩽ x ⩽ b 0 ,  其它  p(x)= \begin{cases}\frac{1}{b-a}, & a \leqslant x \leqslant b \\ 0, & \text { 其它 }\end{cases} p(x)={ b−a1​,0,​a⩽x⩽b 其它 ​

分布函数为：
F ( x ) = { 0 , x < a x − a b − a , a ⩽ x < b 1 , x ⩾ b F(x)= \begin{cases}0, & x<a \\ \frac{x-a}{b-a}, & a \leqslant x<b \\ 1, & x \geqslant b\end{cases} F(x)=⎩⎪⎨⎪⎧​0,b−ax−a​,1,​x<aa⩽x<bx⩾b​

exp:


a = float(0)
b = float(1)
#numpy.linspace()函数用于在线性空间中以均匀步长生成数字序列
x = np.linspace(a,b)
y = np.full(shape=len(x),fill_value=1/(b-a))
#np.full构造一个数组
plt.plot(x,y,"b",linewidth=2)
plt.ylim(0,1,2)
plt.xlim(-1,2)
plt.xlabel('X')
plt.ylabel('p(x)')
plt.title('uniform distribution')
plt.show()

在这里插入图片描述

指数分布

p ( x ) = { λ e − λ x , x ⩾ 0 0 , x < 0 p(x)=\left\{\begin{aligned} \lambda e^{-\lambda x}, & x \geqslant 0 \\ 0, & x<0 \end{aligned}\right. p(x)={ λe−λx,0,​x⩾0x<0​
F ( x ) = { 1 − e − λ x , x ⩾ 0 0 , x < 0 F(x)= \begin{cases}1-\mathrm{e}^{-\lambda x}, & x \geqslant 0 \\ 0, & x<0\end{cases} F(x)={ 1−e−λx,0,​x⩾0x<0​

lam = float(1.5)
x = np.linspace(0,15,100)
y = lam*np.e**(-lam*x)

plt.plot(x,y,"b",linewidth=2)
plt.xlim(-5,10)
plt.xlabel('X')
plt.ylabel('p(x)')
plt.title('指数分布')
plt.show()

在这里插入图片描述

高斯分布

在这里插入图片描述

from sympy import *
from sympy.abc import mu,sigma
x = symbols('X')
p_x = 1/(sqer(2*pi)*sigma)*E**(-(x-mu)**2/(2*sigma**2))
integrate(p_x,(x,-∞,x))

在这里插入图片描述

import math
mu = float(0)
mul = float(2)
sigma1 = float(1)
sigma2 = float(1.25)*float(1.25)
sigma3 = float(0.25)
x = np.linspace(-5, 5, 1000)
y1 = np.exp(-(x - mu)**2 / (2 * sigma1**2)) / (math.sqrt(2 * math.pi) * sigma1)
y2 = np.exp(-(x - mu)**2 / (2 * sigma2**2)) / (math.sqrt(2 * math.pi) * sigma2)
y3 = np.exp(-(x - mu)**2 / (2 * sigma3**2)) / (math.sqrt(2 * math.pi) * sigma3)
y4 = np.exp(-(x - mu1)**2 / (2 * sigma1**2)) / (math.sqrt(2 * math.pi) * sigma1)
plt.plot(x,y1,"b",linewidth=2,label=r'$\mu=0,\sigma=1$') 
plt.plot(x,y2,"orange",linewidth=2,label=r'$\mu=0,\sigma=1.25$') 
plt.plot(x,y3,"yellow",linewidth=2,label=r'$\mu=0,\sigma=0.5$') 
plt.plot(x,y4,"b",linewidth=2,label=r'$\mu=2,\sigma=1$',ls='--') 
plt.axvline(x=mu,ls='--')
plt.text(x=0.05,y=0.5,s=r'$\mu=0$')
plt.axvline(x=mu1,ls='--')
plt.text(x=2.05,y=0.5,s=r'$\mu=2$')
plt.xlim(-5,5)
plt.xlabel('X')
plt.ylabel('p (x)')
plt.title('normal distribution')
plt.legend()
plt.show()

改变mu

在这里插入图片描述
在这里插入图片描述
改变σ

在这里插入图片描述

指数分布计算

from scipy.stats import expon #指数分布
x = np.linspace(0.01,10,1000)
plt.plot(x,expon.pdf(x),'r-',lw=5,alpha=0.6,label='expon pdf')
 # pdf表示求密度函数值
 # cdf表示求分布函数值
plt.xlabel("X")
plt.ylabel("p (x)")
plt.legend()
#plt.legend创建图例
plt.show()

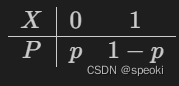
在这里插入图片描述
在这里插入图片描述
(1)0-1分布
在这里插入图片描述
在这里插入图片描述

(2)二项分布

在这里插入图片描述
(3)泊松分布
在这里插入图片描述

泊松分布计算

# 对比不同的lambda对泊松分布的影响
import math
# 构造泊松分布列的计算函数
def poisson(lmd,x):
    return pow(lmd,x)/math.factorial(x)*math.exp(-lmd)
x = [i+1 for i in range(10)]
#定义泊松分布列
lmd1 = 0.8
lmd2 = 2.0
lmd3 = 4.0
lmd4 = 6.0

p_lmd1 = [poisson(lmd1,i) for i in x]
p_lmd2 = [poisson(lmd2,i) for i in x]
p_lmd3 = [poisson(lmd3,i) for i in x]
p_lmd4 = [poisson(lmd4,i) for i in x]

plt.scatter(np.array(x), p_lmd1, c='b',alpha=0.7)
plt.axvline(x=lmd1,ls='--')
plt.text(x=lmd1+0.1,y=0.1,s=r"$\lambda=0.8$")
plt.ylim(-0.1,1)
plt.xlabel("X")
plt.ylabel("p (x)")
plt.title(r"$\lambda = 0.8$")
plt.show()

plt.scatter(np.array(x), p_lmd2, c='b',alpha=0.7)
plt.axvline(x=lmd2,ls='--')
plt.text(x=lmd2+0.1,y=0.1,s=r"$\lambda=2.0$")
plt.ylim(-0.1,1)
plt.xlabel("X")
plt.ylabel("p (x)")
plt.title(r"$\lambda = 2.0$")
plt.show()

plt.scatter(np.array(x), p_lmd3, c='b',alpha=0.7)

plt.axvline(x=lmd3,ls='--')
plt.text(x=lmd3+0.1,y=0.1,s=r"$\lambda=4.0$")
plt.ylim(-0.1,1)
plt.xlabel("X")
plt.ylabel("p (x)")
plt.title(r"$\lambda = 4.0$")
plt.show()

plt.scatter(np.array(x), p_lmd4, c='b',alpha=0.7)
plt.axvline(x=lmd4,ls='--')
plt.text(x=lmd4+0.1,y=0.1,s=r"$\lambda=6.0$")
plt.ylim(-0.1,1)
plt.xlabel("X")
plt.ylabel("p (x)")
plt.title(r"$\lambda = 6.0$")
plt.show()

plt.scatter散点图
axvline函数作用是绘制一条跨越整个子图的垂直线
ylim设置或查询 y 坐标轴范围

from scipy.stats import binom
#scipy.stats包中的binom类对象是表示二项分布的。
n = 10
p = 0.5
x = np.arange(1,n+1,1)
pList = binom.pmf(x,n,p)
#stats.binom.pmf(X,n,p) 用于求概率密度
plt.plot(x,pList,marker='o',alpha = 0.7,linestyle = 'None')

plt.vlines(x, 0, pList)
#绘制数据集
plt.xlabel('随机变量：抛硬币10次')
plt.ylabel('概率')
plt.title('二项分布：n=%d,p=%0.2f' % (n,p))
plt.show()

一维随机变量的数字特征：期望、方差、分位数与中位数

（1）数学期望
分布的位置特征数
离散随机变量：
在这里插入图片描述
连续随机变量：
如果积分有限：

在这里插入图片描述

exp:
在这里插入图片描述
在这里插入图片描述

在这里插入图片描述
(2)标准差与方差
反应随机变量的波动大小

方差
在这里插入图片描述
离散型：
在这里插入图片描述
连续型：
在这里插入图片描述

标准差
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

scipy计算常见分布的均值与方差

# 使用scipy计算常见分布的均值与方差：(如果忘记公式的话直接查，不需要查书了)
from scipy.stats import bernoulli   # 0-1分布
from scipy.stats import binom   # 二项分布
from scipy.stats import poisson  # 泊松分布
from scipy.stats import rv_discrete # 自定义离散随机变量
from scipy.stats import uniform # 均匀分布
from scipy.stats import expon # 指数分布
from scipy.stats import norm # 正态分布
from scipy.stats import rv_continuous  # 自定义连续随机变量

print("0-1分布的数字特征：均值:{}；方差:{}；标准差:{}".format(bernoulli(p=0.5).mean(), 
                                  bernoulli(p=0.5).var(), 
                                  bernoulli(p=0.5).std()))
print("二项分布b(100,0.5)的数字特征：均值:{}；方差:{}；标准差:{}".format(binom(n=100,p=0.5).mean(), 
                                  binom(n=100,p=0.5).var(), 
                                  binom(n=100,p=0.5).std()))
## 模拟抛骰子的特定分布
xk = np.arange(6)+1
pk = np.array([1.0/6]*6)
print("泊松分布P(0.6)的数字特征：均值:{}；方差:{}；标准差:{}".format(poisson(0.6).mean(), 
                                  poisson(0.6).var(), 
                                  poisson(0.6).std()))
print("特定离散随机变量的数字特征：均值:{}；方差:{}；标准差:{}".format(rv_discrete(name='dice', values=(xk, pk)).mean(), 
                                  rv_discrete(name='dice', values=(xk, pk)).var(), 
                                  rv_discrete(name='dice', values=(xk, pk)).std()))
print("均匀分布U(1,1+5)的数字特征：均值:{}；方差:{}；标准差:{}".format(uniform(loc=1,scale=5).mean(), 
                                  uniform(loc=1,scale=5).var(), 
                                  uniform(loc=1,scale=5).std()))
print("正态分布N(0,0.0001)的数字特征：均值:{}；方差:{}；标准差:{}".format(norm(loc=0,scale=0.01).mean(), 
                                  norm(loc=0,scale=0.01).var(), 
                                  norm(loc=0,scale=0.01).std()))

lmd = 5.0  # 指数分布的lambda = 5.0
print("指数分布Exp(5)的数字特征：均值:{}；方差:{}；标准差:{}".format(expon(scale=1.0/lmd).mean(), 
                                  expon(scale=1.0/lmd).var(), 
                                  expon(scale=1.0/lmd).std()))

## 自定义标准正态分布
class gaussian_gen(rv_continuous):
    def _pdf(self, x): # tongguo 
        return np.exp(-x**2 / 2.) / np.sqrt(2.0 * np.pi)
gaussian = gaussian_gen(name='gaussian')
print("标准正态分布的数字特征：均值:{}；方差:{}；标准差:{}".format(gaussian().mean(), 
                                  gaussian().var(), 
                                  gaussian().std()))

## 自定义指数分布
import math
class Exp_gen(rv_continuous):
    def _pdf(self, x,lmd):
        y=0
        if x>0:
            y = lmd * math.e**(-lmd*x)
        return y
Exp = Exp_gen(name='Exp(5.0)')
print("Exp(5.0)分布的数字特征：均值:{}；方差:{}；标准差:{}".format(Exp(5.0).mean(), 
                                  Exp(5.0).var(), 
                                  Exp(5.0).std()))

## 通过分布函数自定义分布
class Distance_circle(rv_continuous):                 #自定义分布xdist
    """ 向半径为r的圆内投掷一点，点到圆心距离的随机变量X的分布函数为: if x<0: F(x) = 0; if 0<=x<=r: F(x) = x^2 / r^2 if x>r: F(x)=1 """
    def _cdf(self, x, r):                   #累积分布函数定义随机变量
        f=np.zeros(x.size)                  #函数值初始化为0
        index=np.where((x>=0)&(x<=r))           #0<=x<=r
        f[index]=((x[index])/r[index])**2       #0<=x<=r
        index=np.where(x>r)                     #x>r
        f[index]=1                              #x>r
        return f
dist = Distance_circle(name="distance_circle")
print("dist分布的数字特征：均值:{}；方差:{}；标准差:{}".format(dist(5.0).mean(), 
                                  dist(5.0).var(), 
                                  dist(5.0).std()))

（3）分位数与中位数
累计概率等于p所对应的随机变量取值x为p分位数
F ( x p ) = ∫ − ∞ x p p ( x ) d x = p F\left(x_{p}\right)=\int_{-\infty}^{x_{p}} p(x) \mathrm{d} x=p F(xp​)=∫−∞xp​​p(x)dx=p

在这里插入图片描述
上下侧相互转换转换公式
x p ′ = x 1 − p , x p = x 1 − p ′ x_{p}^{\prime}=x_{1-p}, \quad x_{p}=x_{1-p}^{\prime} xp′​=x1−p​,xp​=x1−p′​
中位数就是P=0.5时的分位数点
F ( x 0.5 ) = ∫ − ∞ x 0.5 p ( x ) d x = 0.5 F\left(x_{0.5}\right)=\int_{-\infty}^{x_{0.5}} p(x) \mathrm{d} x=0.5 F(x0.5​)=∫−∞x0.5​​p(x)dx=0.5
在这里插入图片描述
中位数和均值可以综合说明数据的分布
均值会受到极端数据的影响

使用python计算标准正态分布的0.25，0.5（中位数），0.75，0.95分位数点。

from scipy.stats import norm
print("标准正态分布的0.25分位数：",norm(loc=0,scale=1).ppf(0.25))   # 使用ppf计算分位数点
print("标准正态分布的0.5分位数：",norm(loc=0,scale=1).ppf(0.5))
print("标准正态分布的0.75分位数：",norm(loc=0,scale=1).ppf(0.75))
print("标准正态分布的0.95分位数：",norm(loc=0,scale=1).ppf(0.95))

多维随机变量及其联合分布、边际分布、条件分布

（1）n维随机变量
在这里插入图片描述
（1.1）n维随机变量的联合分布函数
在这里插入图片描述
（1.2）n维随机变量的联合密度函数
在这里插入图片描述
在这里插入图片描述

（1.3）多维离散随机变量联合分布列

在这里插入图片描述

# 绘制二维正态分布的联合概率密度曲面图
from scipy.stats import multivariate_normal
from mpl_toolkits.mplot3d import axes3d
# mpl_toolkits.mplot3d画三维图的工具包
x, y = np.mgrid[-5:5:.01, -5:5:.01]  # 返回多维结构
#mgrid用法：返回多维结构
pos = np.dstack((x, y))
#自 x和 y都是二维的，np.dstack通过插入大小为 1 的第三个维度来扩展它们
rv = multivariate_normal([0.5, -0.2], [[2.0, 0.3], [0.3, 0.5]])
# multivariate_normal从多元正态分布中随机抽取样本 的函数
z = rv.pdf(pos)
# pdf求密度函数值
plt.figure('Surface', facecolor='lightgray',figsize=(12,8))
ax = plt.axes(projection='3d')
ax.set_xlabel('X', fontsize=14)
ax.set_ylabel('Y', fontsize=14)
ax.set_zlabel('P (X,Y)', fontsize=14)
ax.plot_surface(x, y, z, rstride=50, cstride=50, cmap='jet')
plt.show()

# 绘制二维正态分布的联合概率密度等高线图
from scipy.stats import multivariate_normal
x, y = np.mgrid[-1:1:.01, -1:1:.01]
pos = np.dstack((x, y))
rv = multivariate_normal([0.5, -0.2], [[2.0, 0.3], [0.3, 0.5]])
z = rv.pdf(pos)
fig = plt.figure(figsize=(8,6))
ax2 = fig.add_subplot(111)
ax2.set_xlabel('X', fontsize=14)
ax2.set_ylabel('Y', fontsize=14)
ax2.contourf(x, y, z, rstride=50, cstride=50, cmap='jet')
plt.show()

（2.1）边际分布函数：
lim ⁡ y → ∞ F ( x , y ) = P ( X ⩽ x , Y < ∞ ) = P ( X ⩽ x ) , \lim _{y \rightarrow \infty} F(x, y)=P(X \leqslant x, Y<\infty)=P(X \leqslant x), y→∞lim​F(x,y)=P(X⩽x,Y<∞)=P(X⩽x),

（2.2）边际密度函数

F X ( x ) = F ( x , ∞ ) = ∫ − ∞ x ( ∫ − ∞ ∞ p ( u , v ) d v ) d u = ∫ − ∞ x p X ( u ) d u F Y ( y ) = F ( ∞ , y ) = ∫ − ∞ y ( ∫ − ∞ ∞ p ( u , v ) d u ) d v = ∫ − ∞ y p Y ( v ) d v \begin{aligned} &F_{X}(x)=F(x, \infty)=\int_{-\infty}^{x}\left(\int_{-\infty}^{\infty} p(u, v) \mathrm{d} v\right) \mathrm{d} u=\int_{-\infty}^{x} p_{X}(u) \mathrm{d} u \\ &F_{Y}(y)=F(\infty, y)=\int_{-\infty}^{y}\left(\int_{-\infty}^{\infty} p(u, v) \mathrm{d} u\right) \mathrm{d} v=\int_{-\infty}^{y} p_{Y}(v) \mathrm{d} v \end{aligned} ​FX​(x)=F(x,∞)=∫−∞x​(∫−∞∞​p(u,v)dv)du=∫−∞x​pX​(u)duFY​(y)=F(∞,y)=∫−∞y​(∫−∞∞​p(u,v)du)dv=∫−∞y​pY​(v)dv​
在这里插入图片描述

# 求边际密度函数 p_{X}(x)
from sympy import *
x = symbols('x')
y = symbols('y')
p_xy = Piecewise((1,And(x>0,x<1,y<x,y>-x)),(0,True))
integrate(p_xy, (y, -oo, oo))   ## 由于0<x<1时候，那么x>-x，即2x

# 求边际密度函数 p_{Y}(y)
integrate(p_xy, (x, -oo, oo))   ## 由于|y|<x,0<x<1时，因此y肯定在(-1,1)

（2.3）边际分布列
x的边际分布列
∑ j = 1 ∞ P ( X = x i , Y = y j ) = P ( X = x i ) , i = 1 , 2 , ⋯ \sum_{j=1}^{\infty} P\left(X=x_{i}, Y=y_{j}\right)=P\left(X=x_{i}\right), \quad i=1,2, \cdots j=1∑∞​P(X=xi​,Y=yj​)=P(X=xi​),i=1,2,⋯

y 的边际分布列。
∑ i = 1 ∞ P ( X = x i , Y = y j ) = P ( Y = y j ) , j = 1 , 2 , ⋯ \sum_{i=1}^{\infty} P\left(X=x_{i}, Y=y_{j}\right)=P\left(Y=y_{j}\right), \quad j=1,2, \cdots i=1∑∞​P(X=xi​,Y=yj​)=P(Y=yj​),j=1,2,⋯
(3)条件分布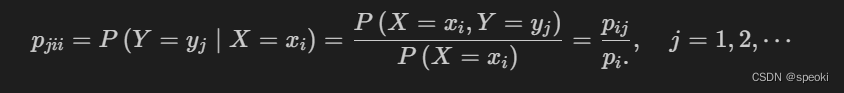
在这里插入图片描述
在这里插入图片描述

在这里插入图片描述

# 求际密度函数 p_{Y}(y)
from sympy import *
from sympy.abc import lamda,m,p,k
x = symbols('x')
y = symbols('y')
f_p = lamda**m/factorial(m)*E**(-lamda)*factorial(m)/(factorial(k)*factorial(m-k))*p**k*(1-p)**(m-k)
summation(f_p, (m, k, +oo))

（3.1）连续场合的全概率公式与贝叶斯公式

在这里插入图片描述

多维随机变量的数字特征：期望向量、协方差与协方差矩阵、相关系数与相关系数矩阵、条件期望

(1)期望向量
n n n 维随机向量为 X = ( X 1 , X 2 , ⋯   , X n ) ′ \boldsymbol{X}=\left(X_{1}, X_{2}, \cdots, X_{n}\right)^{\prime} X=(X1​,X2​,⋯,Xn​)′每个分量的数学期望都存在

数学期望向量（一般为列向量）

E ( X ) = ( E ( X 1 ) , E ( X 2 ) , ⋯   , E ( X n ) ) ′ E(\boldsymbol{X})=\left(E\left(X_{1}\right), E\left(X_{2}\right), \cdots, E\left(X_{n}\right)\right)^{\prime} E(X)=(E(X1​),E(X2​),⋯,E(Xn​))′
（2）协方差与协方差矩阵：
（2.1）协方差：
Cov ⁡ ( X , Y ) = E [ ( X − E ( X ) ) ( Y − E ( Y ) ) ] \operatorname{Cov}(X, Y)=E[(X-E(X))(Y-E(Y))] Cov(X,Y)=E[(X−E(X))(Y−E(Y))]
Cov ⁡ ( X , Y ) = E ( X Y ) − E ( X ) E ( Y ) \operatorname{Cov}(X, Y)=E(X Y)-E(X) E(Y) Cov(X,Y)=E(XY)−E(X)E(Y)

当 Cov ⁡ ( X , Y ) > 0 \operatorname{Cov}(X, Y)>0 Cov(X,Y)>0 时， 称 X X X 与 Y Y Y 正相关

当 Cov ⁡ ( X , Y ) < 0 \operatorname{Cov}(X, Y)<0 Cov(X,Y)<0 时， 称 X X X 与 Y Y Y 负相关

当 Cov ⁡ ( X , Y ) = 0 \operatorname{Cov}(X, Y)=0 Cov(X,Y)=0 时，称 X X X 与 Y Y Y 不相关

若随机变量 X X X 与 Y Y Y 相互独立， 则 Cov ⁡ ( X , Y ) = 0 \operatorname{Cov}(X, Y)=0 Cov(X,Y)=0
Cov ⁡ ( X , Y ) = Cov ⁡ ( Y , X ) . \operatorname{Cov}(X, Y)=\operatorname{Cov}(Y, X) . Cov(X,Y)=Cov(Y,X).
Cov ⁡ ( X , a ) = 0 \operatorname{Cov}(X, a)=0 Cov(X,a)=0
Cov ⁡ ( a X , b Y ) = a b Cov ⁡ ( X , Y ) . \operatorname{Cov}(a X, b Y)=a b \operatorname{Cov}(X, Y) . Cov(aX,bY)=abCov(X,Y).
Cov ⁡ ( X + Y , Z ) = Cov ⁡ ( X , Z ) + Cov ⁡ ( Y , Z ) \operatorname{Cov}(X+Y, Z)=\operatorname{Cov}(X, Z)+\operatorname{Cov}(Y, Z) Cov(X+Y,Z)=Cov(X,Z)+Cov(Y,Z)

对任意二维随机变量 ( X , Y ) (X, Y) (X,Y)， 有
Var ⁡ ( X ± Y ) = Var ⁡ ( X ) + Var ⁡ ( Y ) ± 2 Cov ⁡ ( X , Y ) \operatorname{Var}(X \pm Y)=\operatorname{Var}(X)+\operatorname{Var}(Y) \pm 2 \operatorname{Cov}(X, Y) Var(X±Y)=Var(X)+Var(Y)±2Cov(X,Y)

exp:
p ( x , y ) = { 3 x , 0 < y < x < 1 , 0 ,  其他.  p(x, y)= \begin{cases}3 x, & 0<y<x<1, \\ 0, & \text { 其他. }\end{cases} p(x,y)={ 3x,0,​0<y<x<1, 其他. ​
求 Cov ⁡ ( X , Y ) \operatorname{Cov}(X, Y) Cov(X,Y)。

# 求协方差
from sympy import *
from sympy.abc import lamda,m,p,k
x = symbols('x')
y = symbols('y')
p_xy = Piecewise((3*x,And(y>0,y<x,x<1)),(0,True))
E_xy = integrate(x*y*p_xy, (x, -oo, oo),(y,-oo,oo))
E_x = integrate(x*p_xy, (x, -oo, oo),(y,-oo,oo))
E_y = integrate(y*p_xy, (x, -oo, oo),(y,-oo,oo))
E_xy - E_x*E_y
原网站

版权声明
本文为[speoki]所创，转载请带上原文链接，感谢
https://blog.csdn.net/m0_52024881/article/details/125414887

边栏推荐

猜你喜欢

随机推荐