当前位置:网站首页>【515. 在每个树行中找最大值】
【515. 在每个树行中找最大值】
2022-06-25 07:19:00 【Sugar_wolf】
给定一棵二叉树的根节点 root ,请找出该二叉树中每一层的最大值。
示例1:

输入: root = [1,3,2,5,3,null,9]
输出: [1,3,9]
示例2:
输入: root = [1,2,3]
输出: [1,3]
提示:
- 二叉树的节点个数的范围是 [0,104]
- -231 <= Node.val <= 231 - 1
方法一:深度优先搜索
思路与算法
我们用树的「先序遍历」来进行「深度优先搜索」处理,并用 \textit{curHeight}curHeight 来标记遍历到的当前节点的高度。当遍历到 \textit{curHeight}curHeight 高度的节点就判断是否更新该层节点的最大值。
代码:
class Solution {
public:
void dfs(vector<int>& res, TreeNode* root, int curHeight) {
if (curHeight == res.size()) {
res.push_back(root->val);
} else {
res[curHeight] = max(res[curHeight], root->val);
}
if (root->left) {
dfs(res, root->left, curHeight + 1);
}
if (root->right) {
dfs(res, root->right, curHeight + 1);
}
}
vector<int> largestValues(TreeNode* root) {
if (!root) {
return {
};
}
vector<int> res;
dfs(res, root, 0);
return res;
}
};
执行用时:8 ms, 在所有 C++ 提交中击败了80.00%的用户
内存消耗:21.4 MB, 在所有 C++ 提交中击败了94.52%的用户
复杂度分析
时间复杂度: O(n),其中 n 为二叉树节点个数。二叉树的遍历中每个节点会被访问一次且只会被访问一次。
空间复杂度: O(height)。其中 height 表示二叉树的高度。递归函数需要栈空间,而栈空间取决于递归的深度,因此空间复杂度等价于二叉树的高度。
方法二:广度优先搜索
思路与算法
我们也可以用「广度优先搜索」的方法来解决这道题目。「广度优先搜索」中的队列里存放的是「当前层的所有节点」。每次拓展下一层的时候,不同于「广度优先搜索」的每次只从队列里拿出一个节点,我们把当前队列中的全部节点拿出来进行拓展,这样能保证每次拓展完的时候队列里存放的是下一层的所有节点,即我们是一层一层地进行拓展,然后每一层我们用 maxVal 来标记该层节点的最大值。当该层全部节点都处理完后, maxVal 就是该层全部节点中的最大值。
代码:
class Solution {
public:
vector<int> largestValues(TreeNode* root) {
if (!root) {
return {
};
}
vector<int> res;
queue<TreeNode*> q;
q.push(root);
while (!q.empty()) {
int len = q.size();
int maxVal = INT_MIN;
while (len > 0) {
len--;
auto t = q.front();
q.pop();
maxVal = max(maxVal, t->val);
if (t->left) {
q.push(t->left);
}
if (t->right) {
q.push(t->right);
}
}
res.push_back(maxVal);
}
return res;
}
};
执行用时:8 ms, 在所有 C++ 提交中击败了80.00%的用户
内存消耗:21.5 MB, 在所有 C++ 提交中击败了88.01%的用户
复杂度分析
时间复杂度: O(n),其中 n 为二叉树节点个数,每一个节点仅会进出队列一次。
空间复杂度: O(n),存储二叉树节点的空间开销。
author: LeetCode-Solution
边栏推荐
- UEFI:修复 EFI/GPT Bootloader
- 《树莓派项目实战》第五节 使用Nokia 5110液晶屏显示Hello World
- How to calculate the information entropy and utility value of entropy method?
- 使用apt-get命令如何安装软件?
- 35岁腾讯员工被裁员感叹:北京一套房,存款700多万,失业好焦虑
- Stm32cubemx learning (5) input capture experiment
- 第五天 脚本与UI系统
- June training (day 25) - tree array
- Rank sum ratio (RSR) index calculation
- How is the ISM model analyzed?
猜你喜欢

How to interpret the information weight index?

Overview of image super score: the past and present life of image super score in a single screen (with core code)

Static web server
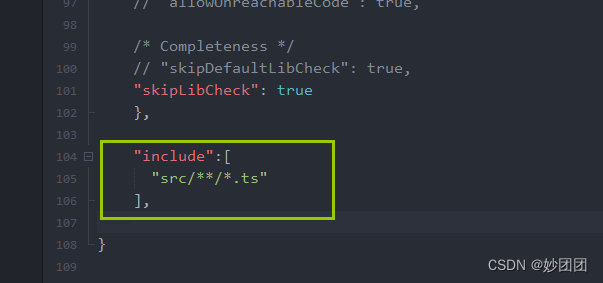
TS environment setup

五分钟快速搭建一个实时人脸口罩检测系统(OpenCV+PaddleHub 含源码)

使用apt-get命令如何安装软件?

How to calculate critical weight indicators?
Internet of things (intelligent irrigation system - Android end)

InfluxDB时序数据库

Stack awareness - stack overflow instance (ret2libc)
随机推荐
After using the remote control of the working machine, problems occurred in the use of the local ROS, and the roscore did not respond
Stack awareness - stack overflow instance (ret2libc)
How to calculate the information entropy and utility value of entropy method?
Software engineering review questions
What are the indicators of VIKOR compromise?
Self made ramp, but it really smells good
Problems caused by Gil problems and Solutions
如何实现一个系统调用
Rank sum ratio (RSR) index calculation
《树莓派项目实战》第五节 使用Nokia 5110液晶屏显示Hello World
4个不可不知的采用“安全左移”的理由
Can I grant database tables permission to delete column objects? Why?
4 raisons inconnues d'utiliser le "déplacement sûr à gauche"
Deep learning series 45: overview of image restoration
What is the role of software validation testing? What is the price of the confirmation test report?
现在网上开通股票账号安全吗?
Incluxdb time series database
如何设计测试用例
What about the exponential smoothing index?
Common action types