【C语言】深度剖析数据在内存中的存储

---

前言

Hello这里是 超人不会飞ke，这么炎热的天，最适合呆在空调房里学习了，小编这几天也是一直沉迷于学习！那么今天想给大家总结一下近几天学习的一些成果，以及分享一些自己的心得体会

本文围绕数据在内存中的存储展开讨论，运用C语言深度剖析数据在内存中究竟是如何存储的，并举一些例题来帮助大家理解和掌握。下面就让我带领大家一起走进计算机的内存大门，修炼我们的“内功心法”吧！！

---

1️⃣ 数据类型介绍

 在C语言中，为了表示生活中各种不同的事物，定义了很多种类型。不仅有我们熟悉的内置类型，还有可以让我们自己发挥的构造类型。不同的类型在内存中的存储也是不同的，这里所指的不同主要是指所占空间大小的不同，当然有时候也可能不同类型看问题的视角不同。
综上所述，我们可以得出c语言中类型的意义：

1. 规定了不同类型使用时在内存中开辟的空间（所占空间大小）
2. 如何看待内存空间的视角

下面让我们来整理归类一下c语言类型吧！

1.整型家族

char（字符类型）
signed char
unsigned char
所占空间大小：1字节
为什么字符类型也被纳入整型家族呢？
因为字符的本质是ASCII码值，这些值是整型，所以其被纳入整型家族

---

short （短整型）
signed short [int]
unsigned short [int]
所占空间大小：2字节

---

int
signed int
unsigned int
所占空间大小：4字节

---

long（长整形）
signed long [int]
unsigned long [int]

在c99标准下还增加了long long长长整型类型，它的大小是八个字节

在这里我们需要注意两点：

1. unsigned为无符号类型（为了定义生活中那些没有负数的数据，c语言定义了带有unsigned的类型，如：身高、体重）；
2. 当我们创建一个类型为short、int、long的变量时，编译器会默认其为有符号的变量（如int则默认为signed int）；
3. 而当我们创建一个类型为char的变量时，编译器不一定会默认其为signed char。不同编译器对其的默认不同。
4. 在我们创建变量时，如果想要表示一个只有正数的数可以创建一个unsigned类型，反之可以创建一个signed类型。

2.浮点数家族

float(精度较低)

---

double(精度较高)

浮点数一般用于表示小数

3.构造类型

数组类型
结构体类型：struct
枚举类型：enum
联合类型：union

4.指针类型

int* pi
char* pc
float* pf
double* pd
void* pv
…

---

2️⃣数据在内存中的存储

那么知道了数据的类型后，接下来让我们来探究一下数据在内存中是如何存储的吧！

我们知道，变量的创建是要在内存中开辟空间的，空间的大小由变量的类型决定。那么，在开辟的这块空间中，数据又是以什么形式存储进去的呢？不同类型的数据的存储方式又有什么不同呢？下面我们将围绕整型数据和浮点型数据的两种内存存储方式展开讨论。

---

1. 整型在内存中的存储

原码、反码、补码

整型在内存中是如何存储的？
为了探究其真相，我们必须先了解下面的概念——
原码、反码、补码：
计算机中的整数有三种2进制表示方法，即原码、反码和补码。三种表示方法均有符号位和数值位两部分，符号位就是二进制序列的第一位，用0表示“正”，用1表示“负”，而数值位，正数的原、反、补码都相同，负整数的三种表示方法各不相同（负整数的原反补码表示方法 具体如下：

1. 原码：直接将数值按照正负数的形式翻译成二进制就可以得到原码；
2. 反码：原码除符号位外按位取反，得到反码；
3. 补码：反码+1得到补码。

---

举个栗子：整型int类型 -6的原码、反码、补码形式如下：

其实，对于整型来说：数据存放内存中其实存放的是补码。例如上面的-6，如果我们创建了一个int类型的变量int a = -6，那么其会根据变量的类型在内存中开辟相应大小的空间（这里变量类型为int则开辟四个字节的空间）。然后再将初始化的数据的补码存入这块空间中。不仅是初始化，在对变量进行赋值时也是一样的道理，只是省去了开辟空间的环节。

如图所示

内存中的地址单元是一个字节，根据类型开辟对应的空间，防止了空间的浪费。我们知道，一个字节是8个比特位，因此每个字节中存入了对应数据的8个比特位，刚好存入了32位。这里要注意的是，局部变量的创建是在内存中的栈区中创建的，而全局变量、静态变量则是在静态区创建的。

为了方便后续分析，我们将二进制序列转换为十六进制，如图（一个十六进制位对应四个二进制位）：

那么问题来了，为什么整型数据存储时存放在内存中的是补码呢？

在计算机系统中，数值一律用补码来表示和存储。原因在于

1. 使用补码，可以将符号位和数值域统一处理
2. 同时，加法和减法也可以统一处理（CPU只有加法器）
3. 此外，补码与原码相互转换，其运算过程是相同的，不需要额外的硬件电路。

解释

1. 用符号位表示数据的正负，可以很好地将符号位和有效位统一进行处理；
2. CPU只有加法器，那么对于减法是如何实现的呢？例如计算1-1，则CPU在计算时则转换为1+(-1)。而对于1+(-1)，如果直接用原码计算，则：
   1+(-1)=00000000000000000000000000000001+10000000000000000000000000000001=10000000000000000000000000000010
   该结果不等于0，我们并不能得到我们想要的结果。而如果用补码计算，则：
   1+(-1)=00000000000000000000000000000001+11111111111111111111111111111111=100000000000000000000000000000000
   而这里进了一位变为33位，溢出了int的空间范围。因此舍弃掉最高位得到结果为0，是我们想要的结果。由此体现出了使用补码存储数据的优越性
3. 这里也是运用补码的巧妙之处。补码原码相互转换的过程是相同的，都是取反加1。
   以-1为例
   
   如图，验证了补码与原码相互转换运算过程是相同的。

---

大小端的介绍

这里我们再来讨论一个问题。看图！

上面我们在画数据存储进内存空间的图解的时候，习惯性地将其按顺序地存放，那么，数据在内存中存放的顺序是怎么样的呢？到底是不是按照我们所画出地这个顺序存放的呢？
这里我们要了解一个概念——大小端，了解了大小端，便能领悟其中的奥秘。

• 大小端是什么？

大小端就是c语言中内存存放数据的两种模式：

• 大端（存储）模式，是指数据的低位保存在内存的高地址中，而数据的高位保存在内存的低地址中；
• 小端（存储）模式，是指数据的低位保存在内存的低地址中，而数据的高位,保存在内存的高地址中。

这里的位，是以字节为单位的，既低字节和高字节组成的字节序，称为大小端字节序。

• 为什么会有大小端？

在c语言中存在许多的类型，如short、int、long…它们的大小都各不相同，比如short的大小是2个字节，int的大小是4个字节。多个字节在内存中存放就必然涉及到顺序问题，由于可以有很多种不同的排序方法，c语言便保留了两种：大端模式和小端模式。计算机上的存储模式可能是大端也可能是小端，具体是哪一个由硬件决定。

这里我们举十六进制序列11223344在内存中的存储为例，画图助解：


可以看到，两种存储模式是截然相反的。大端存储更符合人类思考的逻辑，而小端存储更符号计算机的运行逻辑。

为了加深对大小端的理解，下面我们看一道有关大小端的例题：

设计一个小程序来判断当前机器的字节序

直接上代码

#include <stdio.h>
int check_key()
{
    
	int a = 1;//创建变量a
	char* p = (char*)&a;
	//取a的地址（由指针的知识可知，整型变量a的地址是其四个字节空间中最低字节的地址）
	//并强制类型转换为char*类型，存入指针变量p中
	return *p;//返回p中的值，如果是1则为小端，是0则为大端
}
int main()
{
    
	int ret = check_key();//通过函数的返回值判断大小端
	if (ret == 1)
	{
    
		printf("小端\n");
	}
	else
	{
    
		printf("大端\n");
	}
	return 0;
}

通过调试观察内存可以看到（这里的字节序是用十六进制表示的），a中的数据确实以小端模式存储。所以当我们通过改变指针类型为char*访问其第一个字节中的数据时，得到的是1的最低字节01。如果是大端存储我们将得到00。

---

整型提升、算术转换及例题

掌握了数据在内存中的存储，我们知道了数据如何往内存中“放”。那么，有“放”肯定会有“拿”，当我们想要提取并使用内存中的整型数据时，又有什么奇妙之处呢？想要了解这里面的奥妙，我们需要掌握这些概念：整型提升、算术转换

1.整型提升

• 什么是整型提升？

C的整型算术运算总是至少以缺省整型类型的精度来进行的。为了获得这个精度，表达式中的字符和短整型操作数在使用之前被转换为普通整型，这种转换称为整型提升。

• 整型提升的意义？

表达式的整型运算要在CPU的相应运算器件内执行，CPU内整型运算器(ALU)的操作数的字节长度一般就是int的字节长度，同时也是CPU的通用寄存器的长度。因此，即使两个char类型的相加，在CPU执行时实际上也要先转换为CPU内整型操作数的标准长度。通用CPU（general-purpose CPU）是难以直接实现两个8比特字节直接相加运算（虽然机器指令中可能有这种字节相加指令）。所以，表达式中各种长度可能小于int长度的整型值，都必须先转换为int或unsigned int，然后才能送入CPU去执行运算。

• 什么时候会发生整型提升？

1. char、short类型的操作数在进行表达式运算之前会先发生整型提升
2. 在printf函数中，当char、short类型的数据以%d或%u的格式打印 时，会先发生整型提升（以%u格式打印时转换为unsigned int)

• 如何进行整型提升？

*负数的整形提升：char c1 = -1; 变量c1的二进制位(补码)中只有8个比特位：1111111 ，因为 char 为有符号的 char， 所以整型提升时，高位补充符号位，即为1，提升之后的结果是 ：
11111111111111111111111111111111
*正数的整形提升：char c2 = 1; 变量c2的二进制位(补码)中只有8个比特位： 00000001 ，因为 char 为有符号的char，所以整型提升时，高位补充符号位，即为0，提升之后的结果是 ：
00000000000000000000000000000001

*无符号整形提升： 高位补0

举两个栗子

例一：

#include <stdio.h>
int main()
{
    
	char a = 1;
	char b = -1;
	char c = a + b;
	//00000001 -> 00000000000000000000000000000001 a
	//11111111 -> 11111111111111111111111111111111 b
	//a+b == 00000000000000000000000000000000
	//00000000 -> c
	return 0;
}

a和b的值被提升为普通整型，再进行运算。运算后得到的结果也为普通整型，普通整型存入c中，需要发生截断后再存入，既存入c的值为0
截断：将占字节大的数据类型赋给占字节小的数据类型时，由于小数据类型空间不足，容纳不下大数据类型，因此会发生截断。截断的规则是：取大数据类型的低位存入小数据类型中。（如这里的int赋给char，既取int的低8位赋给char）


例二：

#include <stdio.h>
int main()
{
    
	char a = 0xb6;
	short b = 0xb600; 
	int c = 0xb6000000; 
	//
	if (a == 0xb6)
		printf("a"); 
	if (b == 0xb600)
		printf("b"); 
	if (c == 0xb6000000)
		printf("c"); 
	return 0;
}

当变量作为关系操作符、逻辑操作符的操作数时，也是一种表达式运算，也可能会发生整型提升。
这里a,b要进行整形提升,但是c不需要整形提升 a,b整形提升之后,变成了负数,所以表达式 a==0xb6 , b==0xb600结果是假，返回值是0，但是c不发生整形提升,则表达式 c==0xb6000000 的结果是真.
所程序输出的结果是: c

---

2.算术转换

如果某个操作符的各个操作数属于不同的类型，那么除非其中一个操作数的转换为另一个操作数的类型，否则操作就无法进行。下面的层次体系称为寻常算术转换。

如果某个操作数的类型在上面这个列表中排名较低（箭头指向由低到高），那么首先要转换为另外一个操作数的类型后执行运算。

举个栗子

#include <stdio.h>
int main()
{
    
	int a = -4;
	unsigned int b = 8;
	printf("%d", a + b);
	return 0;
}

图解如下：

注意 算术转换要合理，否则可能会导致精度丢失

float f = 3.14;
int num = f;//隐式转换，会有精度丢失

---

3.例题

掌握了整型提升和算术转换这两个“内功”之后，下面让我们练练几道题巩固一下吧


一、

// 输 出 什 么 ？ 
#include <stdio.h> 
int main()
{
    
	char a = -1;
	signed char b = -1;
	unsigned char c = -1;
	printf("a=%d,b=%d,c=%d", a, b, c);
	return 0;
}

运行结果




二、

// 输 出 什 么 ？ 
#include <stdio.h> 
int main()
{
    
	char a = -128;
	printf("%u\n", a);
	return 0;
}

运行结果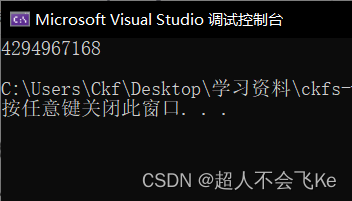




三、

// 输 出 什 么 ？ 
#include <stdio.h> 
int main()
{
    
	char a = 128;
	printf("%u\n", a);
	return 0;
}

运行结果

结果与第二题相同




四、

//输出什么？
#include <stdio.h> 
int main()
{
    
	int i = -20;
	unsigned int j = 10;
	printf("%d\n", i + j);
}

运行结果




五、

#include <stdio.h>
//结果是什么?
int main()
{
    
	unsigned int i;
	for (i = 9; i >= 0; i--) 
	{
    
		printf("%u\n", i);
	}
}

因为变量i的类型是unsigned int，所以它不可能小于0，也就是说循环不可能结束。因此该程序将会进入死循环。

六、

//输出结果为?
#include <stdio.h>
int main()
{
    
	char a[1000];
	int i;
	for (i = 0; i < 1000; i++)
	{
    
		a[i] = -1 - i;
	}
	printf("%d", strlen(a));
	return 0;
}

要弄懂这道题，首先要知道char类型数据的大小范围。下面画图助解：

我们知道，char类型占1个字节，既8个比特位，8个比特位可以表示的数字有2^8也就是256个。如图从0开始，顺时针绕一圈为char能表示的所有数字。这里面有一个特例，10000000这个补码如果转换为原码，则为100000000，多了一位，溢出了char的空间。因此，c语言规定在char类型中，10000000表示-128。综上所述，char类型数据的大小范围是 -128~127。

掌握了这个知识点我们再来看这道题：

运行结果

想要知道其他整型类型的大小范围，可以通过查询limits.h头文件，进行更多的了解。需要我们记住的是char的好兄弟 unsigned char，他的范围是0~255。

以下是该头文件中的代码

#pragma once
#define _INC_LIMITS

#include <vcruntime.h>

#pragma warning(push)
#pragma warning(disable: _VCRUNTIME_DISABLED_WARNINGS)

_CRT_BEGIN_C_HEADER

#define CHAR_BIT 8
#define SCHAR_MIN (-128)
#define SCHAR_MAX 127
#define UCHAR_MAX 0xff

#ifndef _CHAR_UNSIGNED
    #define CHAR_MIN SCHAR_MIN
    #define CHAR_MAX SCHAR_MAX
#else
    #define CHAR_MIN 0
    #define CHAR_MAX UCHAR_MAX
#endif

#define MB_LEN_MAX 5
#define SHRT_MIN (-32768)
#define SHRT_MAX 32767
#define USHRT_MAX 0xffff
#define INT_MIN (-2147483647 - 1)
#define INT_MAX 2147483647
#define UINT_MAX 0xffffffff
#define LONG_MIN (-2147483647L - 1)
#define LONG_MAX 2147483647L
#define ULONG_MAX 0xffffffffUL
#define LLONG_MAX 9223372036854775807i64
#define LLONG_MIN (-9223372036854775807i64 - 1)
#define ULLONG_MAX 0xffffffffffffffffui64

#define _I8_MIN (-127i8 - 1)
#define _I8_MAX 127i8
#define _UI8_MAX 0xffui8

#define _I16_MIN (-32767i16 - 1)
#define _I16_MAX 32767i16
#define _UI16_MAX 0xffffui16

#define _I32_MIN (-2147483647i32 - 1)
#define _I32_MAX 2147483647i32
#define _UI32_MAX 0xffffffffui32

#define _I64_MIN (-9223372036854775807i64 - 1)
#define _I64_MAX 9223372036854775807i64
#define _UI64_MAX 0xffffffffffffffffui64

#ifndef SIZE_MAX
    // SIZE_MAX definition must match exactly with stdint.h for modules support.
    #ifdef _WIN64
        #define SIZE_MAX 0xffffffffffffffffui64
    #else
        #define SIZE_MAX 0xffffffffui32
    #endif
#endif

#if __STDC_WANT_SECURE_LIB__
    #ifndef RSIZE_MAX
        #define RSIZE_MAX (SIZE_MAX >> 1)
    #endif
#endif

_CRT_END_C_HEADER

#pragma warning(pop) // _VCRUNTIME_DISABLED_WARNINGS

---

2. 浮点型在内存中的存储

我们已经掌握了整型数据在内存中的存储。而在c语言中，还有另外一个家族——浮点数家族，它们的存储方式和整型数据的存储方式一样吗？如果不一样又是怎么的一种模式呢？下面我们就这几个问题展开讨论。

浮点数，既小数，用于表示我们生活中的各种小数。常见的浮点数有3.14159，1E10。浮点数家族包括：float, double, long double。

下面我们用一个例子来引入浮点数在内存中的存储：

#include <stdio.h>
int main()
{
    
	int n = 9;
	float* pFloat = (float*)&n;
	printf("n的值为：%d\n", n);
	printf("*pFloat的值为：%f\n", *pFloat);
	//
	*pFloat = 9.0;
	printf("n的值为：%d\n", n);
	printf("*pFloat的值为：%f\n", *pFloat);
	return 0;
}

输出的结果：

从该例子中我们可以得出结论：整型数据和浮点数数据在内存中的存储和提取是不相同的，那么到底是哪里不相同呢？为了探究其中的奥妙，我们必须弄清浮点数在内存中的存储规则：

浮点数在计算机内部的表示方法
详细解读：
根据国际标准IEEE（电气和电子工程协会） 754，任意一个二进制浮点数V可以表示成下面的形式： (-1)^S * M * 2^E

(-1)^S 表示符号位，当S=0，V为正数；当S=1，V为负数。
M 表示有效数字（1≤M<2）
2^E 表示指数位。

举个例子 比如十进制的5.0，其二进制表示为101.0，相当于1.01*2^2
那么根据上述V的表示形式，这里S=0，M=1.01，E=2
比如十进制的5.0，其二进制表示为-101.0，相当于(-1)^1*1.01*2^2
那么根据上述V的表示形式，这里S=1，M=1.01，E=2

IEEE754规定用S, E, M三个数字表示任意一个二进制浮点数，又利用这三个数字，规定了浮点数在内存中的存储模式：

对于32位的浮点数，最高的1位是符号位s，接着的8位是指数E，剩下的23位为有效数字M

对于64位的浮点数，最高的1位是符号位s，接着的11位是指数E，剩下的52位为有效数字M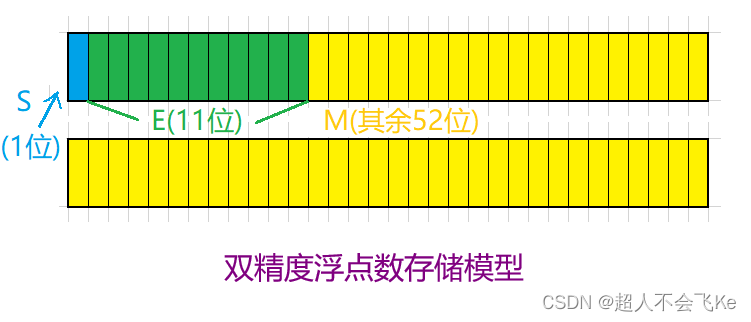

IEEE754对有效数字M和指数E，还有一些特别规定
对于M

前面说过， 1≤M<2 ，也就是说，M可以写成1.xxxxxx的形式，其中xxxxxx表示小数部分。IEEE754规定，在计算机内部保存M时，默认这个数的第一位总是1，因此可以被舍去，只保存后面的xxxxxx部分。比如保存1.01的时候，只保存01，等到读取的时候，再把第一位的1加上去。这样做的目的，是节省1位有效数字。以32位浮点数为例，留给M只有23位，将第一位的1舍去以后，相当于可以保存24位有效数字。
（注：在存储浮点数时，如果M的舍去第一位1后，后面的xxxxxx部分不足23位（或64位），则在后面补0到位数够了为止）
对于指数E

首先，E为一个无符号整数（unsigned int） 这意味着，如果E为8位，它的取值范围为0~255；如果E为11位，它的取值范围为0~2047。但是，我们知道，科学计数法中的E是可以出现负数的，所以IEEE754规定，存入内存时E的真实值必须再加上一个中间数，对于8位的E，这个中间数是127；对于11位的E，这个中间数是1023。 比如，2^10的E是10，所以保存成32位浮点数时，必须保存成10+127=137，即10001001。

---

而当我们从内存中提取出浮点数时，E还可以分为三种情况。


1.E不全为0或不全为1

此时按正常的规则进行取出其浮点数，既指数E减去127（或1023）得到E真实值，再将有效数字M前面补上第一位的1得到真实的M。
比如：
二进制序列0 01111110 00000000000000000000000
可以观察到这个二进制序列有32位，是一个单精度浮点数。
第一步：读取第一位S为0，则该数的浮点数为正数。
第二步：读第一位的后八位，这八位表示的数减去127得到E的真实值E = 01111110 - 01111111 = -1
第三步：读剩余的23位，这23位补上第一位1得到M，则M = 1.00000000000000000000000
因此该数等于 (-1)^0 * 1.00000000000000000000000 * 2^(-1) = 0.1，转化为十进制则为0.5


2.E全为0

这时，浮点数的指数E等于1-127（或者1-1023）即为真实值，有效数字M不再加上第一位的1，而是还原为0.xxxxxx的小数。这样做是为了表示±0，以及接近于0的很小的数字。


3.E全为1

这时，如果有效数字M全为0，表示±无穷大（正负取决于符号位s）

---

OK！了解了浮点数在内存中的存储规则，我们再来分析一下开头引入的例题吧！为什么这里会出现意向不到的结果呢？让我们一步一步仔细分析（分为两部分分析）：

//引例
#include <stdio.h>
int main()
{
    
    //上半部分
	int n = 9;
	float* pFloat = (float*)&n;
	printf("n的值为：%d\n", n);
	printf("*pFloat的值为：%f\n", *pFloat);
	//下半部分
	*pFloat = 9.0;
	printf("n的值为：%d\n", n);
	printf("*pFloat的值为：%f\n", *pFloat);
	return 0;
}

上半部分：





下半部分

由此我们可以得出结论，打印发生异常的原因是我们存入数据和取出数据的方式不同，得到的结果就可能会出乎我们的意料。我们写代码的时候要谨慎小心，和内存“打好交道”，减少bug的出现~

---

总结

今天的分享到这里就结束啦！如有错误，欢迎大佬指正~
这里想分享一句今天看到的一句话：Do what you love, love what you do.
做自己喜欢的事是生活的意义！加油xdm！
如果看到这里不妨给个三连噢~