当前位置:网站首页>deep learning statistical arbitrage
deep learning statistical arbitrage
2022-06-27 10:31:00 【SyncStudy】
deep learning statistical arbitrage
- empirial
- stanford
- Jorge guijarro
- markus
Motivation
- Pair trading
- GM and Ford
- Assumption
- prices are on average similar
- Exploit temporal price different between similiar seests
Three components of statisical arbitarge
- contrict protolio
- trading signal
Foundational problem
Research question
- arbitrage portolios
- arbitarge signals
Contributions
- Novel conceptual framework
- Unified framework
- To compare different statistical arbitrage methods
- Portolio generation
- signal extraction
- allocation decision
- Study each component and compare with conventional models
Novel methods
- statistical factor
- Convolution neural network
Empirical
- substantially outperforms
- sharpe ratios
Parametric models
- PCA
- cOINTEGRATION
- STOCHASTIC CONTROL
- SIMPLE PAIRS TRADING
- INTRACTABLE PARAMETRIC MODELS WITH ml
Model
R n , t = β n , t − 1 T F t + ε R_{n,t}=\beta^T_{n,t-1}F_t+\varepsilon Rn,t=βn,t−1TFt+ε
x : = ε t L : = ( ε n , t − L ) x:=\varepsilon_t^L:=(\varepsilon_{n,t-L}) x:=εtL:=(εn,t−L)
w t − 1 ε = w ε ( θ ( ε t − 1 L ) ) w_{t-1}^\varepsilon=w^\varepsilon(\theta(\varepsilon_{t-1}^L)) wt−1ε=wε(θ(εt−1L))
w t − 1 R = w_{t-1}^R=\frac{}{} wt−1R=
d X t = κ ( μ − X t ) dX_t = \kappa(\mu-X_t) dXt=κ(μ−Xt)
θ i = ∑ j = 1 L W j f i l t e r X j \theta_i=\sum_{j=1}^{L}W_j^{filter}X_j θi=j=1∑LWjfilterXj
W W^{} W
θ C N N + T r a n s ( X ) \theta^{CNN+Trans}(X) θCNN+Trans(X)
y I ( 0 ) = ∑ m = 1 D s i z e W m l o c a l X y_I^{(0)}=\sum_{m=1}^{D_{size}}W_m^{local}X yI(0)=m=1∑DsizeWmlocalX
h i = ∑ I = 1 L α i , I x I ~ h_i=\sum_{I=1}^{L}\alpha_i,I\widetilde{x_I} hi=I=1∑Lαi,IxI
F a m a − F r e n c h F a c t o r Fama-French Factor Fama−FrenchFactor
C N N + T r a n s f o r m CNN+Transform CNN+Transform
α , t α , R 2 \alpha, t_\alpha,R^2 α,tα,R2
t μ t_\mu tμ
w t − 1 = w t − 1 w_{t-1}=\frac{w_{t-1}^{}}{} wt−1=wt−1
L = 60 L=60 L=60
F F N FFN FFN
< 1 % <1\% <1%
T t r a i n = 4 T_{train}=4 Ttrain=4
f a s t − r e v e r s a l fast-reversal fast−reversal
- fast reversal
- early momemtum
- low frequency downturn
- low frequency momentum
- smooth trends or local curvature
- most recent 14 days get more attention for trading decision
- more complex than simple reversal patterns
c o s t ( w t − 1 R , w t − 2 R ) = 0.0005 ∣ ∣ w t − 1 cost(w_{t-1}^R, w_{t-2}^R)=0.0005||w_{t-1} cost(wt−1R,wt−2R)=0.0005∣∣wt−1
B = 7 B=7 B=7
S R = 1 SR=1 SR=1
a r b i t r a g e arbitrage arbitrage
m e a n mean mean
Δ P = P 2 − P 1 \Delta P=P_2-P_1 ΔP=P2−P1
V = ∑ V=\sum V=∑
V = ∣ β 0 + β 1 Δ P ∣ V=|\beta_0+\beta_1\Delta P| V=∣β0+β1ΔP∣
β 0 = c ( μ A − μ B ) \beta_0=c(\mu_A-\mu_B) β0=c(μA−μB)
β 1 = f ( r i s k ) \beta_1=f(risk) β1=f(risk)
E ( V ) = E [ ∣ β 0 + β 1 σ P Z ∣ ] E(V)=E[|\beta_0+\beta_{1\sigma P}Z|] E(V)=E[∣β0+β1σPZ∣]
Z Z Z
N ( 0 , 1 ) N(0,1) N(0,1)
E ( V ) = c o n s t a n t E(V)=constant E(V)=constant
1 1 + ϕ ( h ∣ β 0 ∣ β 1 ) \frac{1}{1+\phi (\frac{h|\beta_0|}{\beta_1})} 1+ϕ(β1h∣β0∣)1
K > S T K>S_T K>ST
K ≤ S τ K \le S_\tau K≤Sτ
K − S τ K-S_\tau K−Sτ
K > S 0 , k = S 0 K>S_0, k=S_0 K>S0,k=S0
m o n e y n e s s = l o g ( K S 0 ) σ τ moneyness=\frac{log(\frac{K}{S_0})}{\sigma \sqrt{\tau}} moneyness=στlog(S0K)
l o n g d a t e d = l a r g e τ long dated = large \tau longdated=largeτ
M o n e y n e s s = l o g ( K S 0 ) σ τ Moneyness = \frac{log(\frac{K}{S_0})}{\sigma\sqrt{\tau}} Moneyness=στlog(S0K)
S P X SPX SPX
3 b i l l i o n 3 billion 3billion
R V t o p t i o n = ∑ i ( r i , t o p t i o n ) 2 RV_t^{option}=\sum_i (r_{i,t}^{option})^2 RVtoption=i∑(ri,toption)2
realized variance
R V t o p t i o n = ∑ i ( r i , t o p t i o n ) 2 RV_t^{option}=\sum_i(r_{i,t}^{option})^2 RVtoption=i∑(ri,toption)2
边栏推荐
- Multi thread implementation rewrites run (), how to inject and use mapper file to operate database
- 嵌入式软件架构设计-模块化
- 并发,并行,异步,同步,多线程,互斥的概念
- 如何在 Methodot 中部署 JupyterLab?
- [tcapulusdb knowledge base] tcapulusdb Model Management Introduction
- Error im002 when Oracle connects to MySQL
- [cloud enjoys freshness] community weekly · vol.68- Huawei cloud recruits partners in the field of industrial intelligence to provide strong support + business realization
- Working at home is more tiring than going to work at the company| Community essay solicitation
- Explain the imaging principle of various optical instruments in detail
- [noodle classic] Yunze Technology
猜你喜欢

Mail system (based on SMTP protocol and POP3 protocol -c language implementation)

【TcaplusDB知识库】Tmonitor单机安装指引介绍(二)

【HCIE-RS复习思维导图】- STP
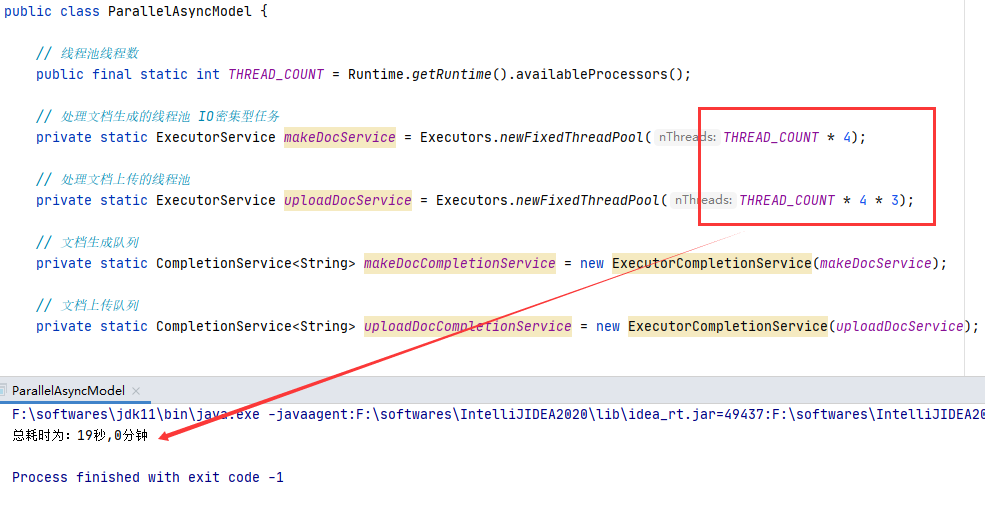
Future & CompletionService

What basic functions are required for live e-commerce application development? What is the future development prospect?

用户认证技术

Audiotrack and audiolinker
![leetcode:522. Longest special sequence II [greed + subsequence judgment]](/img/43/9b17e9cb5fee9d14c2986a2141889d.png)
leetcode:522. Longest special sequence II [greed + subsequence judgment]

CPU设计(单周期和流水线)

21:第三章:开发通行证服务:4:进一步完善【发送短信,接口】;(在【发送短信,接口】中,调用阿里云短信服务和redis服务;一种设计思想:BaseController;)
随机推荐
CPU design (single cycle and pipeline)
go-zero微服务实战系列(七、请求量这么高该如何优化)
C语言学习-Day_05
Mongodb cross host database copy and common commands
【TcaplusDB知识库】Tmonitor单机安装指引介绍(一)
导师邀请你继续跟他读博,你会不会立马答应?
Mail system (based on SMTP protocol and POP3 protocol -c language implementation)
Ci/cd automatic test_ 16 best practices for CI / CD pipeline to accelerate test automation
User authentication technology
堆-堆排序-TopK
C language learning day_ 05
2-4 installation of Nessus under Kali
Frequently asked questions about closures
以后发现漏洞,禁止告诉中国!
学习笔记之——数据集的生成
C any() and aii() methods
Win10 shortcut key sorting
Go zero micro Service Practice Series (VII. How to optimize such a high demand)
红包雨: Redis 和 Lua 的奇妙邂逅
unity shadow 和outline组件动态加载出错解决方案、问题深入分析