Selective sort method

Simple selection sort

The basic idea

Each time, select a record with the smallest keyword as the current record to be determined .

Algorithmic thought

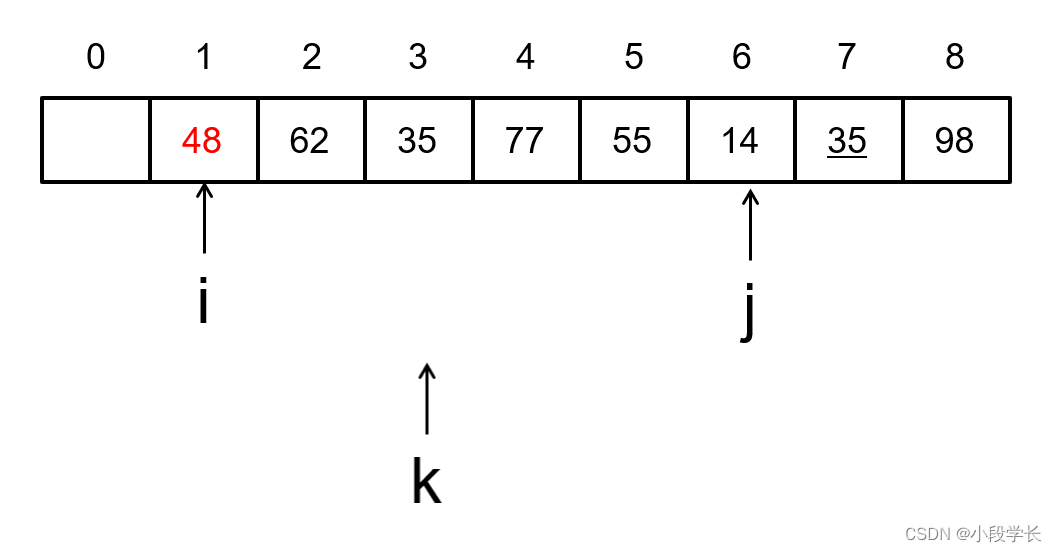
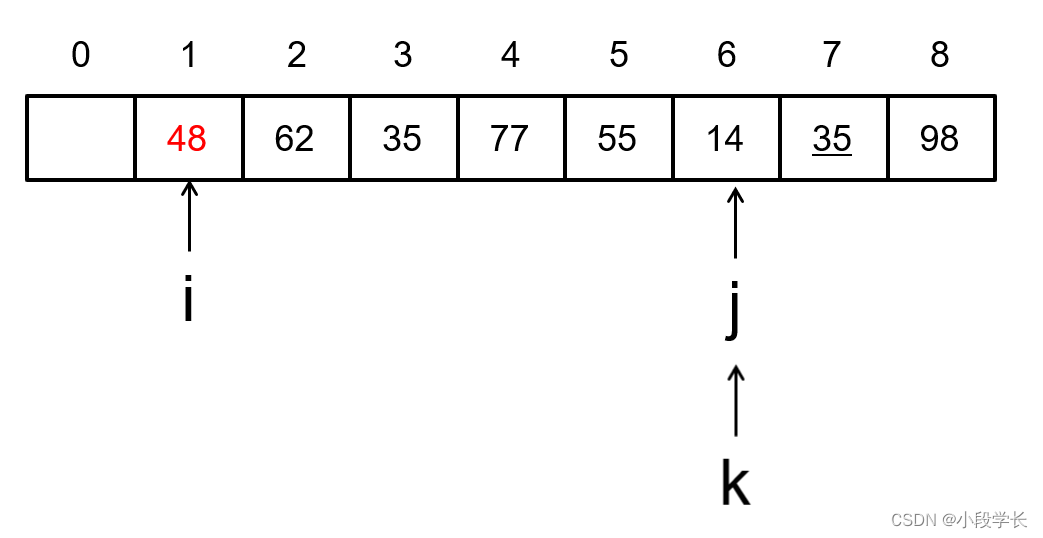
The first trip ： Select a record with the smallest keyword , And exchange with the first record .
The second trip ： In the rest of the sequence , Select a record with the smallest keyword , And exchange with the second record .
Repeat total n-1 You can finish sorting in one time .
The first i Trip to , Make sure No i A record
k Is the subscript of the maximum value
j Subscript for search

Algorithm analysis

The best situation ： Orderly , Comparison times n(n-1)/2, Number of moves 0, The time complexity is O(n2).
The worst ： The first record has the largest keyword , Other records are in order , Comparison times n(n-1)/2, Number of moves 3(n-1), The time complexity is O(n2).
Spatial complexity ：O(1).
stability ： unstable .

Tree selection sort

Key points of algorithm improvement

Simple selection sort ： from n To find the record with the smallest keyword among the elements, you need to compare n-1 Time .
From the rest n-1 Whether it is necessary to find the record with the second smallest keyword in the records n-2 This comparison ？
improvement ： Save the size relationship in the comparison process . Requires space overhead .

Algorithmic thought

First, sort the n Compare the keywords of two records , Take out the smaller ones , And then in the selected n/2 Of the smaller , Then compare the smaller one , So again and again , Until the smallest keyword is selected .
Select the secondary keyword for , Set the keyword value of the leaf node corresponding to the minimum key record to ∞, Then compare the keyword of the leaf node with that of its sibling node , Modify the value from the leaf node to each node on the root path , Then the value of the root node is the minor keyword .

Select the minimum keyword 27

Algorithm analysis

set up n A leaf record , Depth is h Full binary tree .
In addition to selecting the minimum keyword , The selection of other smaller keywords needs to be compared h-1 Time , The comparison times for each keyword selected are log2n .
The time complexity of the comparison is O(nlog2n).
The number of times the record is moved does not exceed the number of comparisons , Therefore, the total time complexity is O(nlog2n).
The space complexity is O(n). Added n-1 Nodes .
stability ： Stable . When the left and right children are equal , Give priority to the left child , Ensure that the priority relationship remains unchanged .

Heap sort

Key points of algorithm improvement

Tree sorting ： Auxiliary space n-1 Record size .
Heap order ： Auxiliary space 1 Record size .

The concept of heaps

A complete binary tree is a sequential table ( Array mode ) Storage , Each node ( That is, each record ) Keywords of meet the conditions ：r[i].key>=r[2i].key also r[i].key>=r[2i+1].key A complete binary tree of is called a large root heap .
That is, the keyword of the node of the large root heap is greater than or equal to the keyword of its left and right children .
conversely , It's called a root heap .
Heap sort is an application of the complete binary tree sequential structure .
example : Determine whether the following two sequences are heaped ？
{ 98,77,35,62,55,14,35,48 }
{ 14,48,35,62,55,98,35,77 }

Rebuild heap

Problem solved ： When the top record changes , How to rebuild the heap .
Method ：“ Screening ” Law .
Auxiliary space ： A record size space .
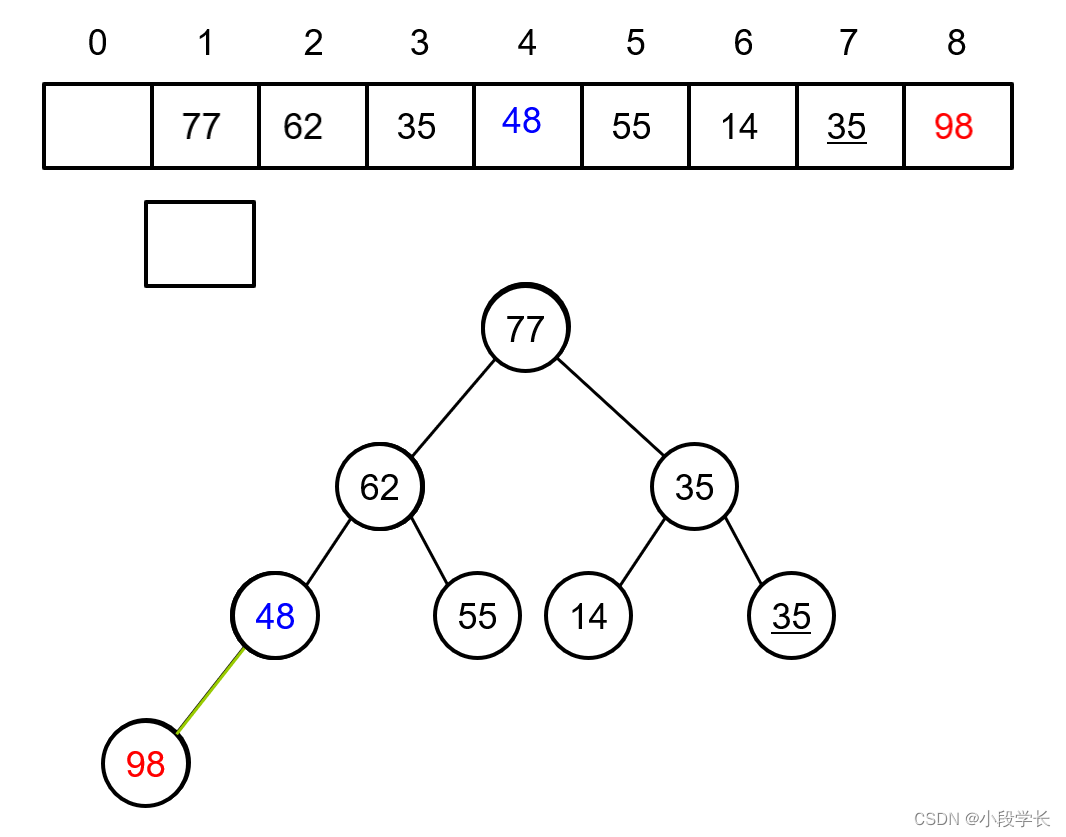
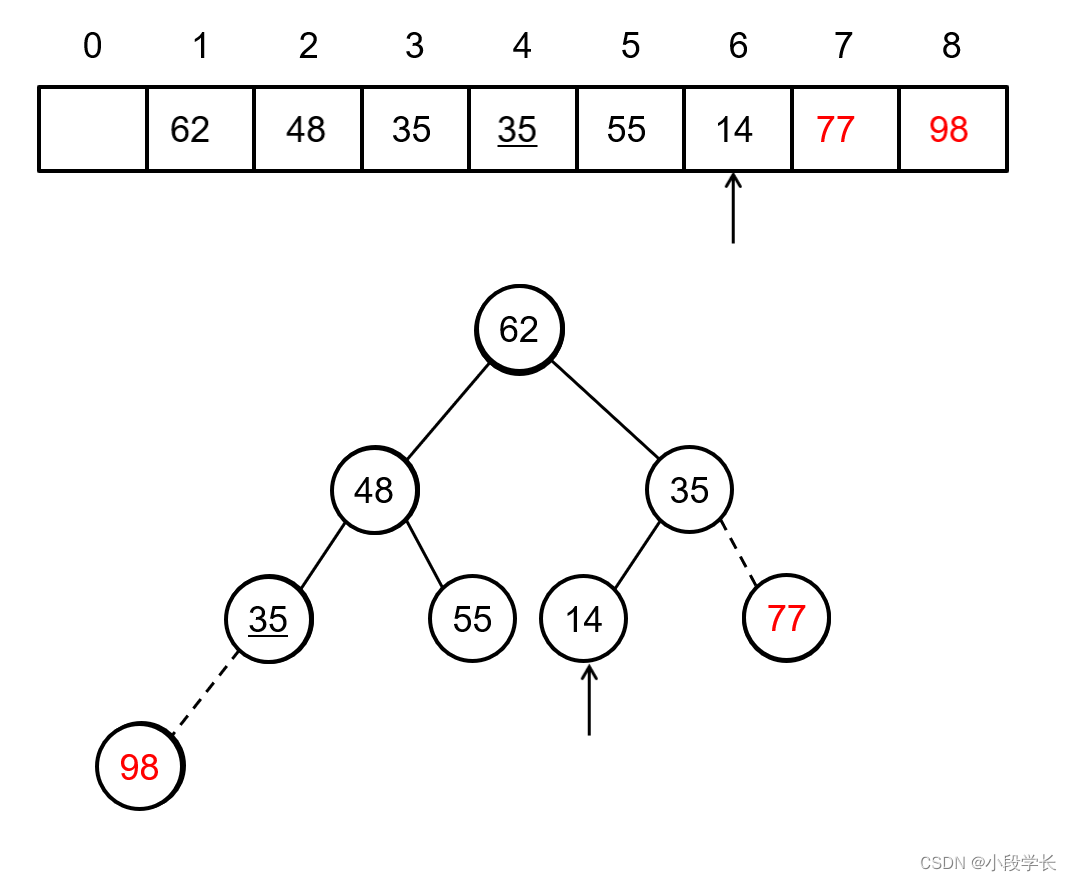
for example ： Known initial sequence of keywords { 98,77,35,62,55,
14,35,48 }, The corresponding is shown in the figure below . After exchanging the top record with the bottom record , Give the adjustment and build process of the remaining records .
Top tail exchange , Before remaining n-1 A record , Determined the n Records with the largest keyword .

Jianchu pile

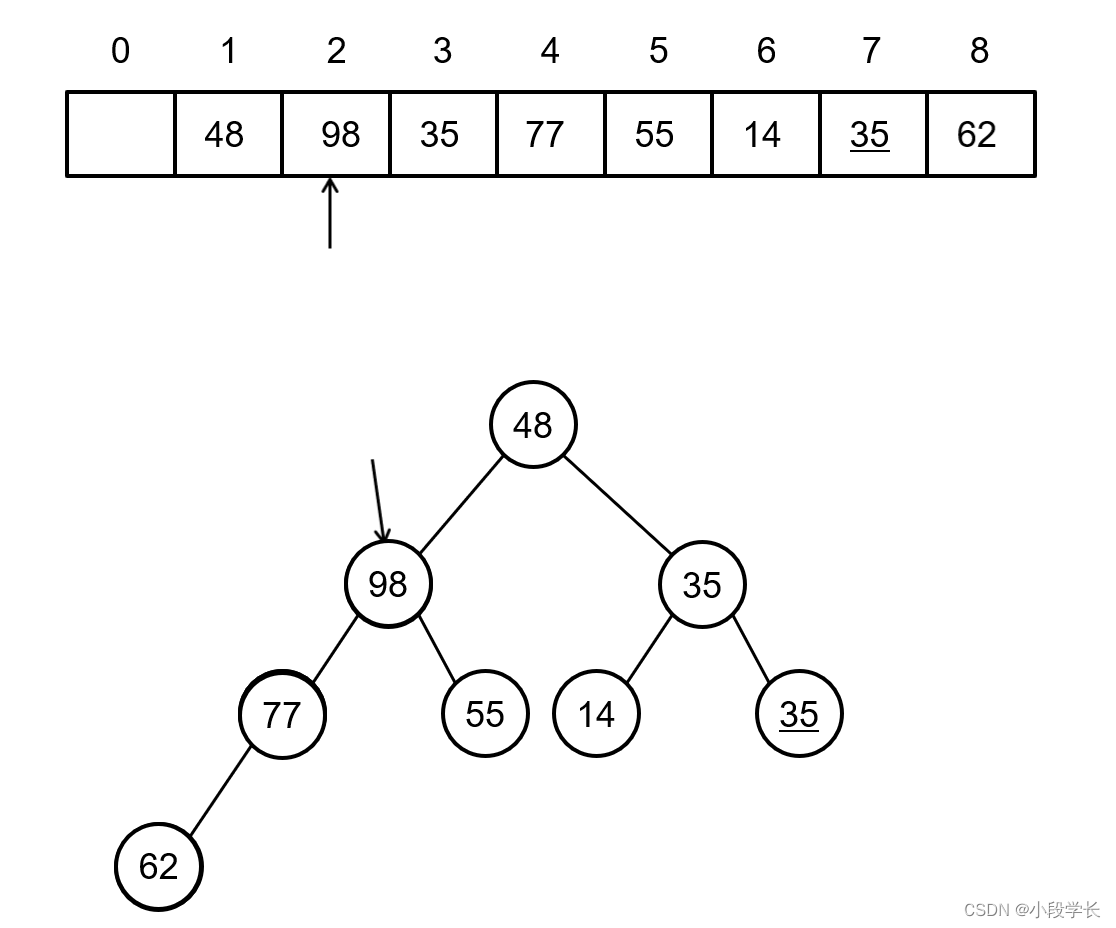
Problem solved ： Adjust any sequence to heap .
Algorithmic thought ： A single node binary tree is a heap . The sequence number of leaf node is greater than n/2.
“ Screening ” Just start from page n/2 Start with a node , Until the root node .
for example ： Known initial sequence of keywords { 48,62,35,77,55,
14,35,98 }, Adjust it to heap .

Heap sort

Problem solved ： How to use heap to complete sorting .
It is known that ： The top and bottom records of the heap are exchanged , Before remaining n-1 A record , Determined the n Records with the largest keyword .
Algorithmic thought ：
① Jianchu pile .
② Exchange top and tail records , And rebuild the new heap with the remaining previous records .
③ Repeat step n-1 You can complete the sorting .

Algorithm analysis

Time complexity ：O(nlog2n).
Spatial complexity ：O(1).
stability ： unstable .
Welcome to join me for wechat exchange and discussion （ Please note csdn Add ）