Theoretical analysis of countermeasure training: adaptive step size fast countermeasure training

PaperWeekly original ·  author |  guiguzi

introduction

This paper is about the theoretical analysis of confrontation training , At present, confrontation training and its variants have been proved to be the most effective means to resist confrontation attacks , But the process of confrontation training is extremely slow, which makes it difficult to expand to such areas as ImageNet On such a large data set , And in the process of confrontation training, the model is often over fitted . In this paper , The author studies this phenomenon from the perspective of training samples , The research shows that the over fitting phenomenon of the model depends on the training samples , And the training samples with larger gradient norm are more likely to lead to catastrophic over fitting . therefore , The author puts forward a simple but effective method , That is, adaptive step counter training （ATAS）.

ATAS Learning to adjust the training sample adaptive step size which is inversely proportional to its gradient norm . Theoretical analysis shows that ,ATAS It converges faster than the commonly used non adaptive algorithm , When evaluating various counter disturbances ,ATAS It can always reduce the over fitting phenomenon of the model , And the algorithm in CIFAR10、CIFAR100 and ImageNet And other data sets to achieve higher model robustness .

Paper title ：

Fast Adversarial Training with Adaptive Step Size

Thesis link ：

https://arxiv.org/abs/2206.02417

Background knowledge

FreeAT Firstly, a method of fast confrontation training is proposed , Through batch repeated training and simultaneously optimizing model parameters and resisting disturbance .YOPO A similar strategy is used to optimize the countermeasure loss function . later , The one-step method is proved to be better than FreeAT and YOPO More effective . If you carefully adjust the super parameters , With random start FGSM（FGSM-RS） It can be used to generate anti disturbance in one step , To train the robust network model .ATTA The method is to take advantage of the mobility of the counter samples , Use the clean sample as the initialization of the counter sample , The specific optimization form is as follows ：

among , Said in the first   In the middle of the round   Samples Generated countermeasure samples .ATTA Show and FGSM-RS Fairly robust accuracy .SLAT And FGSM Simultaneous disturbance of input and potential values , Ensure more reliable performance . These one-step methods can lead to disastrous over fitting , This means that the model is right PGD The robustness accuracy of the attack will suddenly drop to close to 0, And yes FGSM The robust accuracy of the attack is improved rapidly .

To prevent over fitting of the model ,FGSM-GA Added a regularizer , Used to align the direction of the input gradient . Another work studies this phenomenon from the perspective of loss function , It is found that the excessive phenomenon of the model is the result of the high distortion of the loss surface , A new algorithm is proposed to solve the model over fitting by checking the loss value along the gradient direction . However , Both algorithms need to be better than FGSM-RS and ATTA More computation .

The paper algorithm

According to previous studies , The internal maximized step size in the counter training objective function plays an important role in the performance of the single step attack method . Too large a step size will cause all FGSM The counter disturbance is attracted near the classification boundary , Leading to catastrophic overfitting , therefore PGD The robustness accuracy of the classifier against multi-step attack will be reduced to zero . However , You can't simply reduce the step size , Because as shown in the first and second figures in the following figure, we can find , Increasing the step size can enhance the resistance to attacks and improve the robustness of the model .

In order to strengthen the attack as much as possible and avoid catastrophic over fitting , For samples with large gradient norm , The author uses a small step length to strengthen the attack and prevent the model from over fitting ; For samples with small gradient norm , The author uses stride length to strengthen the attack . therefore , The author uses the moving average of gradient norm ：

To adjust in For samples in the wheel Step size of . yes The initialization , Is the momentum balance factor . And Inversely proportional ：

among Is the predefined learning rate , It's a prevention Too large a constant . The author will adapt the step size And FGSM-RS Combination ,FGSM-RS Random initialization against disturbance in internal maximization attack . From the third subgraph of the above figure, we can find , The adaptive step size will not be fitted . Besides , The average step size of the adaptive step size method is even larger than FGSM-RS The fixed step size in is even larger , So it is more aggressive and more robust .

Random initialization limits the disturbance resistance of samples with small step size , This reduces the strength of the attack . Combined with the previous initialization method , The method proposed in this paper ATAS No need for big To achieve the whole Norm ball . For each sample , The author uses adaptive step size And perform the following internal maximization to obtain the countermeasure sample ：

among It's No The counter sample of the wheel , Parameters By sample To update , The formula is as follows ：

Compared with the previous methods that need a lot of computational overhead to solve the catastrophic over fitting problem , Proposed by the paper ATAS Method overhead is negligible ,ATAS Training time and ATTA and FGSM-RS Almost the same .ATAS The detailed algorithm of is as follows ：

stay ImageNet On dataset ATAS The detailed algorithm of is as follows ：

The author analyzes ATAS Method in Convergence under norm , Give the following objective function ：

The min max problem can be formulated as follows ：

among Is in the parameter The optimal countermeasure sample under . The author considers the minimax optimization problem under the conditions of convex concave and smooth , And the loss function The following assumptions are met .

hypothesis 1： Training loss function Satisfy the following constraints ：

1） Is a convex function and In the parameter The bottom is smooth ; and The gradient is in The norm satisfies the following formula ：

among ：

2） Is a concave function and In each sample smooth . stay In the norm sphere and the radius is . For any and ,, And the input gradient satisfies the following formula ：

The average author Step parameter trajectories are approximated to optimality ：

This is the standard technique for analyzing random gradient methods , Convergence gap ：

The upper bound is shown by the following formula ：

lemma 1： Loss function Satisfy assumptions 1, Objective function There is the following convergence gap inequality ：

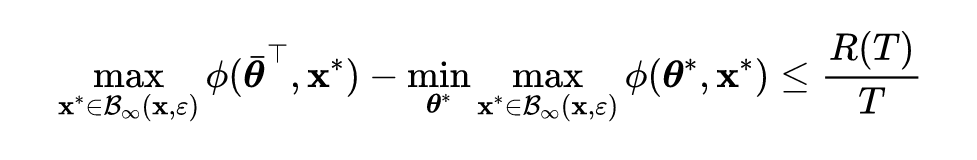
Prove bright ： According to lemma 1 The following inequality can be obtained on the left side of the formula ：

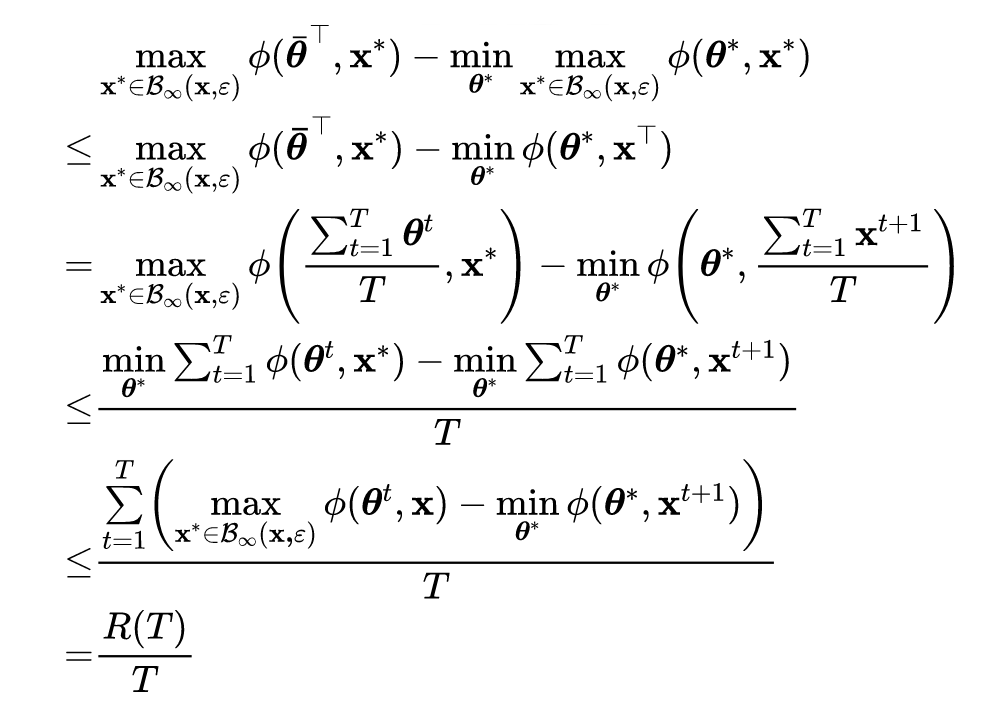
The first and third inequalities follow optimality conditions , The second inequality uses Jensen inequality . In proving the theorem 1 And Theorem 2 when , There are several gradient symbols ：

ATAS The method can also be expressed as an adaptive random gradient descent block coordinate rise method （ASGDBCA）, Steps in Randomly select a sample from the list , For parameters Apply random gradient descent , For input Apply adaptive block coordinate rise . And SGDA Different ,SGDA Update in each iteration All dimensions of ,ASGDBCA Update only Some dimensions of .ASGDBCA First, calculate the pre adjustment parameters by ：

be and Can be optimized to ：

ASGDBCA and ATAS The main difference is . In order to prove ASGDBCA The convergence of , The pre adjustment parameter must be non decreasing . otherwise ,ATAS Maybe not like ADAM That convergence . However ,ADAM The non convergent version of is actually more effective for neural networks in practice . therefore ,ATAS Still use As a pre-regulation parameter .

Theorem 1： Assuming 1 Under the condition of , Yes and , be ASGDBA The bounds of are as follows ：

prove ： Make , In the Step by step ,ASGDBCA from The index of random sampling subscript in is The sample of , So there is ：

Make ：

Expressed as sample All coordinate pre adjustment parameters . Place the expectation on the right above , So there is ：

And there are ：

And SGDBCA The proof process is similar to , There is the following derivation process ：

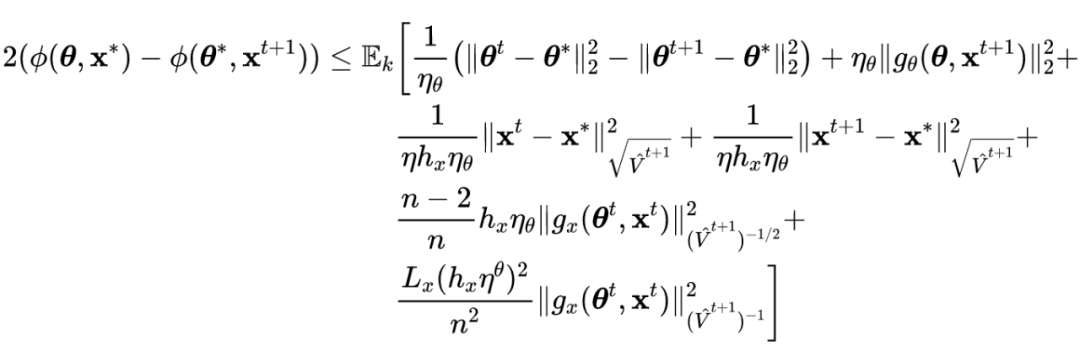
Transform inequality from Sum to , The upper bound of is expressed as ：

and ：

And SGD be similar , Using arithmetic and geometric mean inequality, we know , When Reach the optimum , So there is ：

about The first item of is ：

among Express Of the Coordinate system , So for It is assumed that , So there is ：

about The second item of is ：

among Express pass the civil examinations A coordinate . Yes Sum items , The upper bound of the second term of is ：

The upper bound of the third term of is ：

So there is ：

By combining the above inequalities, we can know ,ASGDBCA The upper bound of is ：

Using arithmetic and geometric mean inequality, we know , When when , The upper bound can reach the minimum ：

Combine and , Then we can see ASGDBCA The upper bound of is ：

ATAS and ATTA The non adaptive version of the random gradient descending block coordinate rising formula is as follows ：

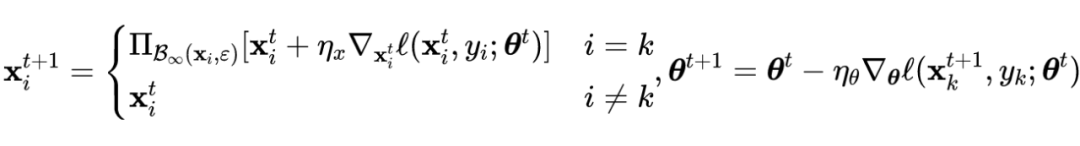
Theorem 2： Assuming 1 Under the condition of , Constant learning rate and , be SGDBCA The upper bound of is as follows ：

prove ： Make , In the Step by step ,SGDBCA Index set from subscript The subscript is randomly sampled in And update the anti disturbance , Then there are the following inequalities ：

therefore ：

Reorder the above inequalities , Then there are ：

Similar can be obtained ：

Calculate the expectation of the left part of the above two formulas to get ：

Then there are ：

and ：

in consideration of and Concavity and convexity of ：

You can get ：

Combining the above inequalities, we can get ：

to update , You can get ：

The above inequalities can be reordered as ：

Both sides of the above inequality are divided by , Then there are ：

Yes The sum of the terms gives the following upper bound ：

The above inequality can be reduced to ：

Using arithmetic and geometric mean, we can get , When and   yes , The optimal upper bound can be obtained ：

Theorem 1 and 2 indicate ASGDBCA Than SGDBCA Convergence is faster . When large ,SGDBCA and ASGDBCA The third term of the interval in is negligible . Considering that their first term is the same , The main difference is that in the second item and

402 Payment Required

About Interval boundary . Their ratios are as follows ：

Cauchy-Schwarz The inequality shows that the ratio is always greater than 1. When With long tail distribution ,ASGDBCA and SGDBCA The gap between them will become even bigger , This shows that ATAS The convergence speed of is relatively faster .

experimental result

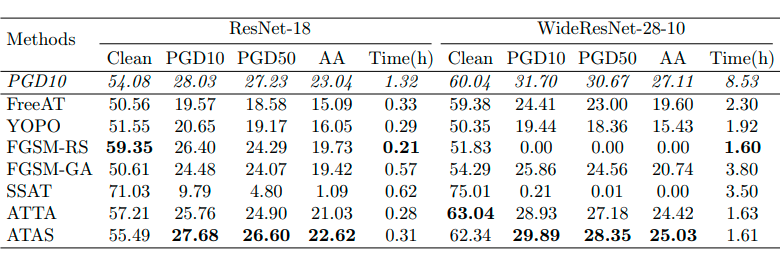
The following three tables show different methods in CIFAR10、CIFAR100 and ImageNet Accuracy and training time on the dataset . It should be noted that , Because of the computational complexity , The author does not have enough computing resources in ImageNet Perform standard confrontation training and SSAT. The author uses two GPU To train ImageNet Model of , about CIFAR10 and CIFAR100, The author in a single GPU Assess training time on . From the following results, we can intuitively find the methods proposed in this paper ATAS Improved in various attacks （ Include PGD10、PGD50 And automatic attacks ） The robustness of the classification model under , And it can be found that catastrophic over fitting of the model can be avoided in training .

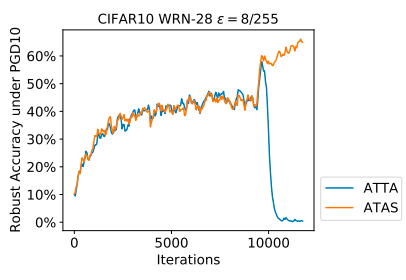
As shown in the figure below , It can be found that equivalence increases ATTA When the training step in ,ATTA and PGD10 The gap between the loss functions becomes smaller . Besides , When the step size is not too large , The robust accuracy of the classification model will increase with the step size . Then we can draw a preliminary conclusion , Larger step sizes also enhance ATTA The ability to attack . However , Large steps can also lead to ATTA Model over fitting occurs .

The method in the paper ATAS The adaptive step size in allows for a larger step size , It will not lead to catastrophic over fitting of the model . As shown in the figure below, the author shows ATTA and ATAS Comparison between . Even if ATAS The step size of is greater than ATTA, It won't look like ATTA In that case, the model is over fitted .

Read more

# cast draft   through Avenue #

  Let your words be seen by more people  

How to make more high-quality content reach the reader group in a shorter path , How about reducing the cost of finding quality content for readers ？ The answer is ： People you don't know .

There are always people you don't know , Know what you want to know .PaperWeekly Maybe it could be a bridge , Push different backgrounds 、 Scholars and academic inspiration in different directions collide with each other , There are more possibilities . 

PaperWeekly Encourage university laboratories or individuals to , Share all kinds of quality content on our platform , It can be Interpretation of the latest paper , It can also be Analysis of academic hot spots 、 Scientific research experience or Competition experience explanation etc. . We have only one purpose , Let knowledge really flow .

  The basic requirements of the manuscript ：

• The article is really personal Original works , Not published in public channels , For example, articles published or to be published on other platforms , Please clearly mark  

• It is suggested that  markdown  Format writing , The pictures are sent as attachments , The picture should be clear , No copyright issues

• PaperWeekly Respect the right of authorship , And will be adopted for each original first manuscript , Provide Competitive remuneration in the industry , Specifically, according to the amount of reading and the quality of the article, the ladder system is used for settlement

  Contribution channel ：

• Send email ：[email protected] 

• Please note your immediate contact information （ WeChat ）, So that we can contact the author as soon as we choose the manuscript

• You can also directly add Xiaobian wechat （pwbot02） Quick contribution , remarks ： full name - contribute

△ Long press add PaperWeekly Small make up

Now? , stay 「 You know 」 We can also be found

Go to Zhihu home page and search 「PaperWeekly」

Click on 「 Focus on 」 Subscribe to our column

·