当前位置:网站首页>Pymoo学习 (4): 多标准决策
Pymoo学习 (4): 多标准决策
2022-07-23 14:12:00 【因吉】
1 多标准决策
在获取一组非支配解后,可以由决策者决定保留一些甚至是单个的解。这个针对多目标问题的决策过程也称为多标准决策 (Multi-criteria decision making, MCDM)。尽管Pymoo的主要精力放在优化上,其也依然提供了一些初级工具来找到一个合适的解。
一个双目标优化的示意可以从https://inkiyinji.blog.csdn.net//article/details/125914306中找到,其给出了Pareto最优解的示意:
需要注意不同目标的值的尺度可能差距很大,需要对其进行标准处理。如果没有标准化,横坐标所对应的优化目标将目标搜索空间中的任何距离计算,因为它的规模更大。处理不同尺度的目标是任何多目标算法的固有部分,而一种常见的标准化方法是使用所谓的理想和最低点。
出于决策和概括目的,我们假设理想和最低点 (也称为边界点) 和Pareto前沿) 是未知的。因此,这些点可以近似为:
相应代码为:
import matplotlib.pyplot as plt
# 理想点和最低点
approx_ideal = F.min(axis=0)
approx_nadir = F.max(axis=0)
plt.figure(figsize=(7, 5))
plt.tight_layout()
plt.scatter(F[:, 0], F[:, 1], s=30, facecolors='none', edgecolors='blue')
plt.scatter(approx_ideal[0], approx_ideal[1], facecolors='none', edgecolors='red', marker="*", s=100, label="Ideal Point (Approx)")
plt.scatter(approx_nadir[0], approx_nadir[1], facecolors='none', edgecolors='black', marker="p", s=100, label="Nadir Point (Approx)")
plt.title("Search Space")
plt.legend()
plt.show()
基于理想和最低点,可以获取缩放后的Pareto最优解:
代码如下:
import matplotlib.pyplot as plt
# 理想点和最低点
approx_ideal = F.min(axis=0)
approx_nadir = F.max(axis=0)
nF = (F - approx_ideal) / (approx_nadir - approx_ideal)
fl = nF.min(axis=0)
fu = nF.max(axis=0)
print(f"Scale f1: [{
fl[0]}, {
fu[0]}]")
print(f"Scale f2: [{
fl[1]}, {
fu[1]}]")
plt.figure(figsize=(7, 5))
plt.scatter(nF[:, 0], nF[:, 1], s=30, facecolors='none', edgecolors='blue')
plt.title("Objective Space")
plt.show()
2 Compromise编程
另一种决策方法是使用分解函数,其需要定义反映用户意愿的权重向量。向量中的权重值只能是正浮点数,和为1,向量长度等于目标数。
对于当前的双目标优化,假设权重为:
weights = np.array([0.2, 0.8])
导入分解函数:
from pymoo.decomposition.asf import ASF
decomp = ASF()
当前使用的分解函数是ASF,其应当被最小化,所以选择从所有解决方案中计算出的最小ASF值:
i = decomp.do(nF, 1/weights).argmin()
此时的权重为1/weights。对于ASF,存在数值除法和数值相乘两种方式。在pymoo中,我们进行不体现用户标准的思想的划分。因此,需要应用逆运算,这将在后续介绍,目前需要知道关于分解函数的决策是至关重要的。
此时,我们可以在原始尺度上表示找到的最优解:
代码如下:
plt.figure(figsize=(7, 5))
plt.scatter(F[:, 0], F[:, 1], s=30, facecolors='none', edgecolors='blue')
plt.scatter(F[i, 0], F[i, 1], marker="x", color="red", s=200)
plt.title("Objective Space")
plt.show()
3 伪权重
伪权重同样用于找到一个更优的解,第 i i i个目标的伪权重给定为:
w i = ( f i m a x − f i ( x ) ) / ( f i m a x − f i m i n ) ∑ m = 1 M ( f m m a x − f m ( x ) ) / ( f m m a x − f m m i n ) w_i=\frac{(f_i^{max}-f_i(x))/(f_i^{max}-f_i^{min})}{\sum_{m=1}^M(f_m^{max}-f_m(x))/(f_m^{max}-f_m^{min})} wi=∑m=1M(fmmax−fm(x))/(fmmax−fmmin)(fimax−fi(x))/(fimax−fimin)该方程计算关于每个目标 i i i的最差解的归一化距离。对于非凸Pareto前沿,伪权重不对应于使用加权和进行优化的结果。而对于凸Pareto前沿,伪权重表示目标空间中的位置:
代码如下:
from pymoo.mcdm.pseudo_weights import PseudoWeights
i = PseudoWeights(weights).do(nF)
plt.figure(figsize=(7, 5))
plt.scatter(F[:, 0], F[:, 1], s=30, facecolors='none', edgecolors='blue')
plt.scatter(F[i, 0], F[i, 1], marker="x", color="red", s=200)
plt.title("Objective Space")
plt.show()
参考文献
边栏推荐
猜你喜欢

软件质量体系之思
Tips and tricks for Neural Networks 深度学习训练神经网络的技巧总结(不定期更新)

PMP每日一练 | 考试不迷路-7.23

VSCode PIO创建工程失败分析和解决办法

Tips and tricks for neural networks deep learning and training skills summary (updated from time to time)

软件配置 | Anaconda下载、安装及环境配置和卸载

SSD: Single Shot MultiBox Detector

Notes on Microcomputer Principle and technical interface

无心剑英汉双语诗006.《致爱妻》
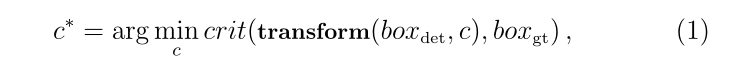
Acquisition of positional reliability in accurate target detection
随机推荐
Tensorflow2.x actual combat series softmax function
opencv之打开摄像头、边缘检测
ROS2自学笔记:Rviz可视化工具
MATLAB基础
Solution for iPhone unable to open openv** file
Using "soup.h1.text" crawler to extract the title will be one more\
TOPSIS法(MATLAB)
sprintf和cv::putText
Priyanka Sharma, general manager of CNCF Foundation: read CNCF operation mechanism
灰色预测(MATLAB)
Pinduoduo app product details interface to obtain activity_ ID value (pinduoduo activity_id interface)
【31. 走迷宫(BFS)】
移动、电信、联通:5G To B的花式解法
Heartless sword English Chinese bilingual poem 006. to my wife
Pinia (pineapple)
【mysql集群故障恢复】
Leetcode-168.excel table column name
Solve data functions should return an object (property "visible" must be accessed with "$data.visible")
Pyinstaller+InstallForge多文件项目软件打包
通用分页实现