当前位置:网站首页>树
树
2022-07-23 13:41:00 【码道人】
基本术语与概念
树的定义(嵌套的定义)
树(Tree)是n (n≥0)个结点的有限集。若n=0,称为空树;若n> 0,则它满足如下两个条件:
- 有且仅有一个特定的称为根(Root)的结点;
- 其余结点可分为m (m≥0)个互不相交的有限集T1, T2, T3, ...Tm,其中每一个集合本身又是一棵树,并称为根的子树(SubTree)。
以下并不是树
节点之间的关系
两个节点之间的路径(只能从上往下),路径长度(经过几条边)
结点、树的属性描述
属性:
- 结点的层次(深度) ——从上往下数(默认从1开始,也有书上从0开始)
- 结点的高度——从下往上数
- 树的高度(深度) ——总共多少层
- 结点的度——有几个孩子(分支),分支节点度>0,叶子节点度=0
- 树的度——各结点的度的最大值
有序树,无序树,森林
有序树——逻辑上看,树中结点的各子树从左至右是有次序的,不能互换(例如家谱)
无序树——逻辑上看,树中结点的各子树从左至右是无次序的,可以互换
具体看你用树存什么,是否需要用结点的左右位置反映某些逻辑关系
森林:森林是m (m>=0)棵互不相交的树的集合
树的性质
- 节点数=总度数+1
- m叉树和度为m的树
- 度为m的树第i层至多有m^{i-1} 个结点(i>=1)
- 高度为h的m叉树至多有个frac{m^h-1}{m-1}结点。(等比数列求和)
- 具有n个结点的m叉树的最小高度为log_m(n(m-1)+ 1)向上取整,用前一个性质证明
二叉树
基本概念
二叉树是n (n>=0) 个结点的有限集合:
- 或者为空二叉树,即n=0。
- 或者由一个根结点和两个互不相交的被称为根的左子树和右子树组成。左子树和右子树又分别是一棵二叉树。
特点:
- 每个结点至多只有两棵子树
- 左右子树不能颠倒(二叉树是有序树)
几个特殊的二叉树
满二叉树:一棵高度为h,且含有2^h- 1个结点的二叉树
特点:
- 只有最后一层有叶子结点
- 不存在度为1的结点
- 按层序从1开始编号,结点i的左孩子为2i,右孩子为2i+1.结点i 的父节点为i/2取整(加里有的话)
完全二叉树:当且仅当其每个结点都与高度为h的满二叉树中编号为1~n的结点一一对应时,称为 完全二叉树
特点:
- 只有最后两层可能有叶子结点
- 最多只有一个度为1的结点
- 按层序从1开始编号,结点i的左孩子为2i,右孩子为2i+1.结点i 的父节点为i/2取整(加里有的话)
- i<=n/2为分支节点,i>n/2为叶子节点
二叉排序树
空二叉树,或者是具有如下性质的二叉树:
- 左子树上所有结点的关键字均小于根结点的关键字:
- 右子树上所有结点的关键字均大于根结点的关键字。
- 左子树和右子树又各是一棵二叉排序树。
平衡二叉树
树上任一结点的左子树和右子树的深度之差不超过1。
二叉树的性质
- 设非空二又树中度为0,1,2的结点个数分别为n0,n1和n2,则n0=n2+1(叶子结点比二分支结点多一个)(节点数=总度数+1)
- 二叉树第i层至多有2^{i-1}个结点(i>=1)
- 高度为h的二叉树至多有2^h-1个结点(即满二叉树)
- 具有n个(n>0)结点的完全二叉树的高度h为log2(n+1)向上取整或log2n+1向下取整,(2^{h-1}
- 对于完全二叉树,可以由的结点数n推出度为0、1和2的结点个数为n0、n1 和n2,完全二叉数最多只有一个度为1的结点,即n1=0或1,同时n0+n2为奇数,若完全二叉树有2k个个结点则必有n1=1, n1=k, n2=k-1
二叉树的存储结构
顺序存储
定义一个长度为MAX的数组tree,按照从上至下、丛左至右的顺序依次存储完全二叉树中的各个结点
struct TreeNode{
eletype value;//节点中数据元素
bool Isempty;//节点是否为空
}
TreeNode tree[MAX];几个重要的基本操作:(注意这里数组下标为0处空缺)
- i的左孩子——2i
- i的右孩子—— 2i+1
- i的父节点——li/2向下取整
- i所在的层次-- log2(n+1)向上取整或log2n+1向下取整
若完全二叉树中共有n个结点,则
- 判断i是否有左孩子?—— 2i <= n
- 判断i是否有右孩子?——2i+1<=n
- 判断i是否是叶子/分支结点? ——i> [n/2]
对于一般的二叉树,为了让数组下标可以反映二叉树节点之间的逻辑关系,只能添加一些不存在的空节点,让其每个节点与完全二叉树的节点对应。
因此,二叉树的顺序存储结构,只适合存储完全二叉树
链式存储
struct BiNode{
eletype date;
BiNode *rchild,*lchild;
};二叉树的遍历
三种遍历方式
先序遍历:根左右(NLR)
中序遍历:左根右(LNR)
后序遍历:左右根(LRN)
抓住根节点
先序遍历
创建二叉树
#include <iostream>
using namespace std;
typedef struct node{
char data;
struct node *lchild,*rchild;
}*BitTree;
//先序遍历的方式创建二叉树
void CreatBitTree(BitTree &T) {
char c;
cin >> c;
if (c == '0') T = NULL;
else {
T = new node;
T->data = c;
CreatBitTree(T->lchild);
CreatBitTree(T->rchild);
}
}输出二叉树
void PreOrderTraverse(BitTree T) {
if (T != NULL) {
cout << T->data << ' ';
PreOrderTraverse(T->lchild);
PreOrderTraverse(T->rchild);
}
}
先序遍历非递归算法
void PreOrderTraverse1(BiTree T) { //非递归先序遍历
if (T == NULL) {
return;
}
LinkStack S;
initStack(S);//初始化链栈
BiTree P = T;//P为工作结点
while (P != NULL || !isEmpty(S)) { //P不空且栈非空
if (P != NULL) {
visit(P);//访问当前结点
push(S, P);//当前结点入栈,因为右子树还未访问
P = P->lchild;
} else {
pop(S, P);//左子树已为空,出栈
P = P->rchild;//访问右子树
}
}
}中序遍历
二叉树按照中序输出
void InOrderTraverse(BitTree T) {
if (T != NULL) {
InOrderTraverse(T->lchild);
cout << T->data << ' ';
InOrderTraverse(T->rchild);
}
} 中序遍历非递归算法
void InOrderTraverse1(BiTree T) { //中序遍历
if (T == NULL) {
return;
}
LinkStack S;
initStack(S);
BiTree P = T;
while (P != NULL || !isEmpty(S)) {
if (P != NULL) {
push(S, P);
P = P->lchild;
} else {
pop(S, P);
visit(P);
P = P->rchild;
}
}
}后序遍历
二叉树按照后序输出
void PostOrderTraverse(BitTree T) {
if (T != NULL) {
PostOrderTraverse(T->lchild);
PostOrderTraverse(T->rchild);
cout << T->data << ' ';
}
}
后序遍历非递归算法
void PostOrderTraverse1(BiTree T) { //后序遍历
if (T == NULL) {
return;
}
LinkStack S;
initStack(S);
BiTree P = T;
BiTNode *r = NULL;//记录最近访问过的结点
while (P != NULL || !isEmpty(S)) {
if (P != NULL) {
push(S, P);//左孩子入栈
P = P->lchild;
} else {
GetTop(S, P);//左孩子为空,取栈顶元素
if (P->rchild == r || P->rchild == NULL) {//右孩子已被访问过或没有右孩子
pop(S, P);//出栈
visit(P);//访问
r = P;//更新r
P = NULL;//P置空,以便取下一个栈顶元素
} else {
P = P->rchild;//右孩子存在且未被访问,继续循环
}
}
}
}二叉树的叶子节点个数
int Leaf(BitTree T) {
if (T == NULL) return 0;
if (T->lchild == NULL && T->rchild == NULL) return 1;
return Leaf(T->lchild) + Leaf(T->rchild);
}
3.6 二叉树的深度
int Deepth(BitTree T){
if (T == NULL)return 0;
int x = Deepth(T->lchild);
int y = Deepth(T->rchild);
return max(x,y) + 1; //树的深度=Max(左子树深度,右子树深度)+1
} 层序遍历
算法思想:
- 初始化一个辅助队列
- 根结点入队
- 若队列非空,则队头结点出队,访问该结点,并将其左右孩子插入队尾(如果有的话)
- 重复3直到队列为空
void LevelOrderTraverse(BiTree T) { //层次遍历
LinkQueue Q;
InitQueue(Q); //初始化一个链队,不知道需要多长队列,而且只需要保存指针
BiTree P;
EnQueue(Q, T); //根结点入队
while (!isEmpty(Q)) { //队列非空
DeQueue(Q, P); //队头元素出队
visit(P); //访问队头元素
if (P->lchild != NULL) //左孩子非空
EnQueue(Q, P->lchild); //左孩子入队
if (P->rchild != NULL)//右孩子非空
EnQueue(Q, P->rchild);//右孩子入队
}
}线索二叉树
结点为n的二叉树一共有n-1条有效分支路径,二叉链表中存在2n-(n-1)=n+1个空指针域(线索二叉树就利用了这些空指针域)
typedef struct ThreadNode{
int data;
struct ThreadNode *lchild,*rchild;
int ltag,rtag;//tag==1时是线索
}ThreadNode,*ThreadTree;中序线索化
后继:如果未被线索化(有右孩子)则在右子树最左下方
前驱:如果未被线索化(有左孩子)则在左子树最右下方
//辅助全局变量,用于查找结点p的前驱
BiTNode *p; // p指向目标结点
BiTNode * pre=NULL; //指向当前访问结点的前驱
BiTNode * final=NULL; //用于记录最终结果 //全局变量pre,指向当前访问结点的前驱
ThreadNode *pre=NULL;
//线索二叉树结点
typedef struct ThreadNode{
ElemType data;
struct ThreadNode *lchild,*rchild;int ltag,rtag; //左、右线索标志
}ThreadNode,* ThreadTree;
void visit(ThreadNode *q)
{
if(q->lchild==NULL) //左子树为空,建立前驱线索
{
q->lchild=pre;
q->ltag=1;
}
if(pre!=NULL&&pre->rchild==NULL)i
pre->rchild=q; //建立前驱结点的后继线索
pre->rtag=1;
}
pre=q;
}
//中序遍历二叉树,一边遍历一边线索化
void InThread(ThreadTree T)
{
if(T !=NULL)
{
InThread (T->lchild ) ; //中序遍历左子树
visit(T); //访问根节点
InThread(T->rchild); //中序遍历右子树
}
}
//中序线索化二叉树T
void CreateInThread(ThreadTree T)
{
pre=NULL; //pre初始为NULL
if(T!=NULL) //非空二叉树才能线索化
{
InThread(T); //中序线索化二叉树
if (pre->rchild==NULL)
pre->rtag=1; //处理遍历的最后一个结点
}
}先序线索化
注意:防止出现转圈,如果左孩子是线索化的就不访问
前驱:如果未被线索化(有左孩子),找不到,除非先序遍历一次,如果有指向父节点的指针也可
后继:如果未被线索化(有右孩子)则为左孩子(如果有,否则为右孩子)
//全局变量pre,指向当前访问结点的前驱
ThreadNode *pre=NULL;
//线索二叉树结点
typedef struct ThreadNode{
ElemType data;
struct ThreadNode *lchild,*rchild;int ltag,rtag; //左、右线索标志
}ThreadNode,* ThreadTree;
void visit(ThreadNode *q)
{
if(q->lchild==NULL) //左子树为空,建立前驱线索
{
q->lchild=pre;
q->ltag=1;
}
if(pre!=NULL&&pre->rchild==NULL)i
pre->rchild=q; //建立前驱结点的后继线索
pre->rtag=1;
}
pre=q;
}
//先序遍历二叉树,一边遍历一边线索化
void PreThread(ThreadTree T)
{
if(T !=NULL)
{
visit(T); //访问根节点
if(T->ltag==0) //lchild不是前驱线索,防止转圈
PreThread(T->lchild); //先序遍历左子树
PreThread(T->rchild); //先序遍历右子树
}
}
//先序线索化二叉树T
void CreateInThread(ThreadTree T)
{
pre=NULL; //pre初始为NULL
if(T!=NULL) //非空二叉树才能线索化
{
PreThread(T); //先序线索化二叉树
if (pre->rchild==NULL)
pre->rtag=1; //处理遍历的最后一个结点
}
}后序线索化
//全局变量pre,指向当前访问结点的前驱
ThreadNode *pre=NULL;
//线索二叉树结点
typedef struct ThreadNode{
ElemType data;
struct ThreadNode *lchild,*rchild;int ltag,rtag; //左、右线索标志
}ThreadNode,* ThreadTree;
void visit(ThreadNode *q)
{
if(q->lchild==NULL) //左子树为空,建立前驱线索
{
q->lchild=pre;
q->ltag=1;
}
if(pre!=NULL&&pre->rchild==NULL)i
pre->rchild=q; //建立前驱结点的后继线索
pre->rtag=1;
}
pre=q;
}
//先序遍历二叉树,一边遍历一边线索化
void PostThread(ThreadTree T)
{
if(T!=NULL)
{
PostThread(T->lchild); //后序遍历左子树
PostThread(T->rchild); //后序遍历右子树
visit(T); //访问根节点
}
}
//后序线索化二叉树T
void CreateInThread(ThreadTree T)
{
pre=NULL; //pre初始为NULL
if(T!=NULL) //非空二叉树才能线索化
{
PostThread(T); //后序线索化二叉树
if (pre->rchild==NULL)
pre->rtag=1; //处理遍历的最后一个结点
}
}
树和森林
树的存储结构
双亲表示法(顺序存储)
/*树的双亲表示法结点结构定义*/
#define MAX_TREE_SIZE 100 //树中多种结点树
typedef int TElemType;
typedef struct PTNode //树的结点定义
{
TElemType data; //结点数据
int parent; //双亲位置
}PTNode;
typedef struct //树的类型定义
{
PTNode nodes[MAX_TREE_SIZE]; //结点数组 双亲表示
int r, n; //r是根位置,n是结点数
}PTree;删除某一个节点
- 若为叶子结点
- 直接删除,parent设为-1,n-1
- 将最后一个赋给该节点,n-1
- 若不是叶子结点
- 还需要删除他的孩子
优点:查指定结点的双亲很方便
缺点:查指定结点的孩子只能从头遍历;直接删除带来的空数据导致遍历更慢
注意与二叉树顺序存储的不同
孩子表示法(顺序+链式存储 主要关注孩子结点)
孩子表示法:顺序存储各个节点,每个结点中保存孩子链表头指针
struct CTNode {
int child; //孩子结点在数组中的位置
struct CTNode *next; //下一个孩子
};
typedef struct {
ElemType data;
struct CTNode *firstchild;//第一个孩子
}CTBox;
typedef struct{
CTBox nodes [MAX_TREE_SIZE];
int n, r; //结点数和根的位置
}CTree;
孩子兄弟表示法(链式存储)
typedef int TElemType;
typedef struct CSNode
{
TElemType data;
struct CSNode* firstchild, *rightsib;
}CSNode,*CSTree;优点:可以用我们熟悉的二叉树操作来处理树
树、森林与二叉树的转换
本质:用二叉链表存储森林——左孩子右兄弟
森林中各个树的根节点之间视为兄弟关系
树的遍历
深度优先遍历
先根遍历:若树非空,则先访问根结点,再按照从左到右的顺序遍历根结点的每一棵子树。这个访问顺序与这棵树对应的二叉树的先序遍历顺序相同。
后根遍历:若树非空,则按照从左到右的顺序遍历根结点的每一棵子树,之后再访问根结点。其访问顺序与这棵树对应的二叉树的中序遍历顺序相同。
广度优先遍历
层次遍历:借助队列,参考之前
森林的遍历
先序遍历森林==每棵树先序遍历组合= =转化为二叉树后先序遍历
中序遍历森林==每棵树中序遍历组合= =转化为二叉树后中序遍历
用孩子兄弟表示法存储,这样进行森林的遍历会更熟悉(二叉树的遍历)
哈夫曼树和哈夫曼编码
路径长度:经过边的长度
结点的权:有某种现实含义的数值(如:表示结点的重要性等)
结点的带权路径长度:权重*路径长度
树的带权路径长度:所有叶子结点的带权路径长度之和( WPL, Weighted Path Length)
在含有n个带权叶结点的二叉树中,其中带权路径长度(WPL)最小的二叉树称为哈夫曼树
固定长度编码——每个字符用相等长度的二进制位表示
可变长度编码——允许对不同字符用不等长的二进制位表示
若没有一个编码是另一个编码的前缀,则称这样的编码为前缀编码,非前缀编码在解码时会有歧义
由哈夫曼树得到哈夫曼编码——字符集中的每个字符作为一个叶子结点,各个字符出现的频度作为结点 的权值,根据之前介绍的方法构造哈夫曼树。由于哈夫曼树不唯一,所以哈夫曼编码不唯一
并查集
并查集操作
用互不相交的树,表示多个集合
并查集支持查找以下操作:
- 合并:合并两个集合;
- 查找:判断两个元素是否在同一个集合中。其核心是用一个数组实现
#include <iostream>
#include <set>
using namespace std;
const int MAX = 10;
int father[MAX];//并查集,father[i]表示元素i的父结点
bool flag[MAX] = {false};
int count = 0;
void initUFS() { //初始化
for (int i = 1; i <= MAX; ++i) {
father[i] = i;
}
}
int findFather(int x) {//查找元素x所在集合的根结点,递推写法
while (x != father[x]) {
x = father[x];
}
return x;
}
int findFather1(int x) {//查找元素x所在集合的根结点,递归写法
if (x == father[x]) return x;
else return findFather1(father[x]);
}
void Union(int a, int b) {//合并a和b所在的集合
int fatherA = findFather(a);
int fatherB = findFather(b);
if (fatherA != fatherB)
father[fatherA] = fatherB;
}
int BestfindFather(int x) { //查找根结点优化,路径压缩,将从x开始查到根结点的路径所经过的所有结点的父结点都置为根结点
int a = x;
while (x != father[x]) {
x = father[x];
}
while (a != father[a]) {
int z = a;
a = father[a];
father[z] = x;
}
return x;
}
int main() {
set<int> s;
int n, m;
cin >> n >> m;
initUFS();
for (int i = 0; i < m; ++i) {
int a, b;
cin >> a >> b;
Union(a, b);
}
for (int j = 1; j <= n; ++j) {
s.insert(findFather(j));
}
cout << s.size();
return 0;
}Union操作优化
优化思路:在每次Union操作构建树的时候,尽可能让树不长高高
- 用根节点的绝对值表示树的结点总数
- Union操作,让小树合并到大树
该方法构造的树高不超过log_2n+ 1
Find操作的优化
压缩路径——Find 操作,先找到根节点,再将查找路径上所有结点都挂到根结点下
Union和Find 优化核心思想都是让树尽可能矮
边栏推荐
- 解决data functions should return an object 并(Property “visible“ must be accessed with “$data.visible“)
- Closure of JS
- Bag of tricks for image classification "with convolutional neural networks"
- benthos杂记
- 浏览器四大内核
- 一款非常棒的开源微社区轻论坛类源码
- Tips and tricks for Neural Networks 深度学习训练神经网络的技巧总结(不定期更新)
- Liupeng, vice president of copu: China's open source has approached or reached the world's advanced level in some areas
- opencv之打开摄像头、边缘检测
- tensorflow一层神经网络训练手写体数字识别
猜你喜欢

熵权法优化TOPSIS(MATLAB)

拼多多APP商品详情接口获取activity_id值(拼多多activity_id接口)

一道反序列化的CTF题分享
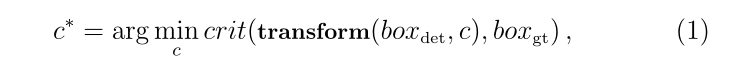
Acquisition of positional reliability in accurate target detection
Compose Canvas饼图效果绘制

主成分分析(MATLAB)

Study note 7 -- traffic environment behavior prediction

【Web漏洞探索】SQL注入漏洞

Detector: detect objects with recursive feature pyramid and switchable atolos convolution

Royal O'Brien, executive director of o3df: open source has no boundaries, and all shared sounds will become the actual direction
随机推荐
深度学习卷积神经网络论文研读-AlexNet
CNCF基金会总经理Priyanka Sharma:一文读懂CNCF运作机制
启牛商学院上面开户安全不
低代码搭建校园信息化管理系统案例分析
IE盒模型和标准盒模型
【Flutter -- 布局】弹性布局(Flex 和 Expanded)
无心剑英汉双语诗006.《致爱妻》
PMP每日一练 | 考试不迷路-7.23
pwn入门(3)堆
Using "soup.h1.text" crawler to extract the title will be one more\
NodeJs实现token登录注册(KOA2)
YOLOV7
面试官:生成订单30分钟未支付,则自动取消,该怎么实现?
Sprintf and cv:: puttext
Tips and tricks for neural networks deep learning and training skills summary (updated from time to time)
分类模型——逻辑回归、Fisher线性判别(SPSS)
How does MySQL query data that is not in the database?
docker 安装redis
灰色预测(MATLAB)
Is it safe for online account managers to open accounts when choosing securities companies in flush