当前位置:网站首页>【二叉樹進階】AVLTree - 平衡二叉搜索樹
【二叉樹進階】AVLTree - 平衡二叉搜索樹
2022-06-23 04:18:00 【CodeWinter】
文章目錄
前言
二叉搜索樹的插入和删除操作都必須先查找,查找效率代錶了二叉搜索樹中各個操作的效率。
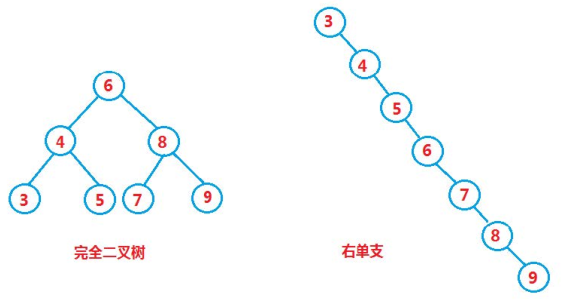
但是二叉搜索樹有其自身的缺陷,假如往樹中插入的元素有序或者接近有序,二叉搜索樹就會退化成單支樹,時間複雜度為O(N),因此 map、set 等關聯式容器的底層結構是對二叉樹進行了平衡處理,即采用平衡二叉搜索樹來實現。
最優情况下,有 n 個結點的二叉搜索樹為完全二叉樹,查找效率為:O(log2N)
最差情况下,有 n 個結點的二叉搜索樹退化為單支樹,查找效率為:O(N)
一、AVL樹
1.1 AVL樹的概念
平衡二叉搜索樹(Self-balancing binary search tree),又稱AVL樹
二叉搜索樹雖可以縮短查找的效率,但如果數據有序或接近有序二叉搜索樹將退化為單支樹,查找元素相當於在順序錶中搜索元素,效率低下。因此,兩比特俄羅斯的數學家G.M.Adelson-Velskii和E.M.Landis在1962年發明了一種解决上述問題的方法:當向二叉搜索樹中插入新結點後,如果能保證每個結點的左右子樹高度之差的絕對值不超過1(超過1需要對樹中的結點進行調整),即可降低樹的高度,從而减少平均搜索長度。
一棵AVL樹,要麼是空樹,要麼是具有以下性質的二叉搜索樹:
每個節點的左右子樹高度之差(簡稱平衡因子 Balance Factor)的絕對值不超過 1 (-1/0/1)
平衡因子 = 右子樹的高度 - 左子樹的高度:用來判斷是否需要進行平衡操作
每一個子樹都是平衡二叉搜索樹

如果一棵二叉搜索樹是高度平衡的,它就是AVL樹。
有n個結點的AVL樹,高度可保持在log2n,其搜索時間複雜度O(log2n)。
思考:為什麼左右子樹高度差不規定成0呢?
因為在2、4等節點數的情况下,不可能做到左右高度相等
1.2 AVL樹節點的定義
AVL樹節點是一個三叉鏈結構,除了指向左右孩子的指針,還有一個指向其父親的指針,數據域是鍵值對,即pair對象,還引入了平衡因子,用來判斷是否需要進行平衡操作。
// AVL樹節點的定義(KV模型)
template<class K, class V>
struct AVLTreeNode
{
pair<K, V> _kv; // 鍵值對
int _bf; // 平衡因子(balance factor) = 右子樹高度 - 左子樹高度
AVLTreeNode<K, V>* _left;
AVLTreeNode<K, V>* _right;
AVLTreeNode<K, V>* _parent; // 雙親指針
// 構造函數
AVLTreeNode(const pair<K, V>& kv)
:_kv(kv)
,_bf(0)
,_left(nullptr)
,_right(nullptr)
,_parent(nullptr)
{
}
};
// AVL樹的定義(KV模型)
template<class K, class V>
class AVLTree
{
typedef AVLTreeNode<K, V> Node;
private:
Node* _root;
public:
// 成員函數
}
1.3 AVL樹 - 插入節點
AVL樹就是在二叉搜索樹的基礎上引入了平衡因子,因此AVL樹也可以看成是二叉搜索樹。那麼AVL樹的插入過程可以分為3步:
- 插入新節點
- 更新樹的平衡因子
- 根據更新後樹的平衡因子的情况,來控制樹的平衡(旋轉操作)
1.3.1 插入新節點
和二叉搜索樹插入方式一樣,先查找,再插入。
// 插入節點
bool AVLTree::Insert(const pair<K, V>& kv)
{
// 如果樹為空,則直接插入節點
if (_root == nullptr)
{
_root = new Node(kv);
return true;
}
// 如果樹不為空,找到適合插入節點的空比特置
Node* parent = nullptr; // 記錄當前節點的父親
Node* cur = _root; // 記錄當前節點
while (cur)
{
if(kv.first > cur->_kv.first) // 插入節點鍵值k大於當前節點
{
parent = cur;
cur = cur->_right;
}
else if(kv.first < cur->_kv.first) // 插入節點鍵值k小於當前節點
{
parent = cur;
cur = cur->_left;
}
else // 插入節點鍵值k等於當前節點
{
return false;
}
}
// while循環結束,說明找到適合插入節點的空比特置了
// 插入新節點
cur = new Node(kv); // 申請新節點
// 判斷當前節點是父親的左孩子還是右孩子
if (cur->_kv.first > parent->_kv.first)
{
parent->_right = cur;
cur->_parent = parent;
}
else
{
parent->_left = cur;
cur->_parent = parent;
}
//...................................
// 這些寫更新平衡因子,和控制樹的平衡的代碼
//...................................
// 插入成功
return true;
}
1.3.2 更新樹的平衡因子
插入「新節點」,從該節點到根所經分支上的所有節點(即祖先節點)的平衡因子都有可能會受到影響,根據不同情况,更新它們的平衡因子:
- 如果插入在「新節點父親」的右邊,父親的平衡因子++(
_bf++)- 如果插入在「新節點父親」的左邊,父親的平衡因子–(
_bf--)
「新節點父親」的平衡因子更新以後,又會分為 3 種情况:
1、如果更新以後,平衡因子是 1 或者 -1(則之前一定為 0),說明父親所在子樹高度變了,需要繼續往上更新。(最壞情况:往上一直更新到根節點)
2、如果更新以後,平衡因子是 0(則之前一定為 1 或者 -1),說明父親所在子樹高度沒變(因為把矮的那邊給填補上了),不需要繼續往上更新。
3、如果更新以後,平衡因子是 2 或者 -2,說明父親所在子樹出現了不平衡,需要旋轉處理,讓它平衡。
代碼如下:
while (parent) // 最壞情况:更新到根節點
{
// 更新新節點父親的平衡因子
if (cur == parent->_left) // 新節點插入在父親的左邊
{
parent->_bf--;
}
else // 新節點插入在父親的右邊
{
parent->_bf++;
}
// 檢查新節點父親的平衡因子
// 1、父親所在子樹高度變了,需要繼續往上更新
if (parent->_bf == 1 || parent->_bf == -1)
{
cur = parent;
parent = cur->_parent;
}
// 2、父親所在子樹高度沒變,不用繼續往上更新
else if (parent->_bf == 0)
{
break;
}
// 3、父親所在子樹出現了不平衡,需要旋轉處理
else if (parent->_bf == 2 || parent->_bf == -2)
{
// 這裏寫對樹進行平衡化操作,旋轉處理的代碼,分為4種情况:
/*................................................*/
// 3.1、父節點的左邊高,右邊低,需要往右旋
if (parent->_bf == -2 && cur->_bf == -1)
{
// 右單旋
treeRotateRight(parent);
}
// 3.2、父節點的右邊高,左邊低,需要往左旋
else if (parent->_bf == 2 && cur->_bf == 1)
{
// 左單旋
treeRotateLeft(parent);
}
// 3.3、父節點的左邊高,且父節點左孩子的右邊高
else if(parent->_bf == -2 && cur->_bf == 1)
{
// 左右雙旋
treeRotateLR(parent);
}
// 3.4、父節點的右邊高,且父節點右孩子的左邊高
else if(parent->_bf == 2 && cur->_bf == -1)
{
// 右左雙旋
treeRotateRL(parent);
}
else // 只有上述4種情况,沒有其它情况,所以這裏直接報錯處理
{
assert(false);
}
break; // 旋轉完成,樹已平衡,退出循環
/*................................................*/
}
// 4、除了上述3種情况,平衡因子不可能有其它的值,報錯處理
else
{
assert(false);
}
}
1.3.3 根據更新後BF的情况,進行平衡化操作
如果在一棵原本是平衡的AVL樹中插入一個新節點,可能造成不平衡,此時必須調整樹的結構,使之平衡化。根據節點插入比特置的不同,AVL樹的旋轉分為4種:
旋轉的本質:在遵循二叉搜索樹的規則下,讓左右均衡,降低整棵樹的高度。
該進行哪種旋轉操作?– 引發旋轉的路徑是直線就是單旋,如果是折線就是雙旋。
注意:此處看到的樹,可能是一顆完整的樹,也可能是一顆子樹。
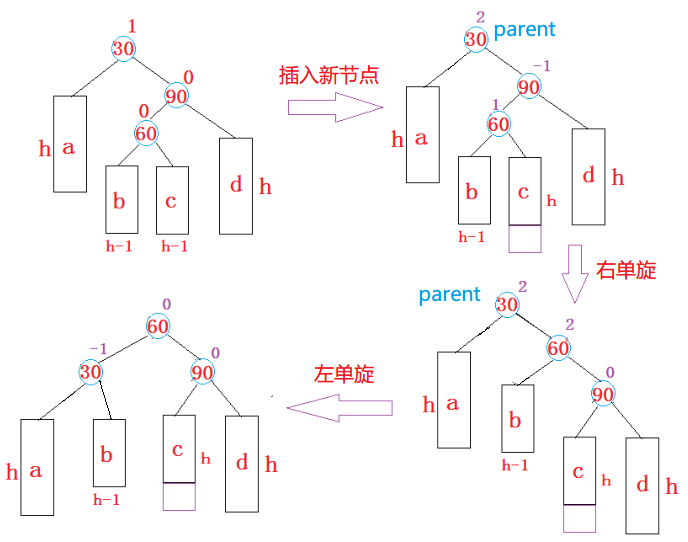
① 右單旋 - 新節點插入較高左子樹的最左側
將新的節點插入到了 parent 左孩子的左子樹上,導致的不平衡的情况。
上圖在插入前,AVL樹是平衡的,新節點插入到30的左子樹(注意:此處不是左孩子)中,30左子樹高度增加了一層,導致以60為根的二叉樹不平衡,要讓60平衡,只能將60左子樹的高度减少一層,右子樹增加一層,即將左子樹往上提,這樣60轉下來,因為60比30大,只能讓其成為30的右子樹,而如果30有右子樹,右子樹根的值一定大於30,小於60,只能讓其成為60的左子樹,旋轉完成後,更新節點的平衡因子即可。
引發右單旋的條件:
- 父親左邊高,右邊低,所以要讓父親往右旋。
- parent 的平衡因子為 -2,parent 左孩子平衡因子為 -1,觀察發現,平衡因子都是負數,說明是左邊高,也說明了==【引發旋轉的路徑是一條直線】==,所以我們要右旋操作。
右單旋操作:
- 讓 subL 的右子樹 subLR 成為 parent 的左子樹(因為 subLR 的右子樹根節點值大於30,小於60)
- 讓 parent 成為 subL 的右子樹(因為60大於30)
- 讓 subL 變成這個子樹的根
- 這一步操作前需要先判斷下:parent 是根節點,還是一個普通子樹
- 如果是根節點,則更新 subL 為新的根
- 如果是普通子樹(可能是某個節點的左子樹,也可能是右子樹,這裏需要判斷下),然後更新 subL 為這個子樹的根節點
- 根據樹的結構,更新 parent 和 subL 的平衡因子為0
在旋轉過程中,更新雙親指針的指向,有以下幾種情况需要考慮:
- subL 的右子樹 subLR 可能存在,也可能為空。(當不為空時才更新 subL 右子樹 subLR 的雙親指針指向)
- 旋轉完成後,subL 的雙親節點,可能是空,也可能是 parent 原先的父節點。(所以更新 subL 的雙親指針前需要判斷下)
代碼如下:
總的來說,就是依次調整 subLR、parent、subL 的比特置和雙親指針的指向。
// 右單旋
void treeRotateRight(Node* parent)
{
// subL:parent的左孩子
// subLR:parent左孩子的右孩子
Node* subL = parent->_left;
Node* subLR = parent->_left->_right;
// 1、讓subL的右子樹subLR成為parent的左子樹
parent->_left = subLR;
// 1.1、如果subLR不為空
if (subLR)
{
subLR->_parent = parent; // 更新subLR的雙親指針,指向parent
}
// 2、讓parent成為subL的右子樹
subL->_right = parent;
// 2.1、記錄下parent的父節點
Node* ppNode = parent->_parent;
// 2.2、更新parent的雙親指針,指向subL
parent->_parent = subL;
// 2.3、判斷parent是不是根節點
// 是根節點
if (parent == _root)
{
_root = subL; // 更新subL為新的根
subL->_parent = nullptr; // 更新subL的雙親指針,指向空
}
// 不是根節點,就是一個普通子樹
else
{
// 判斷parent原先是左孩子還是右孩子
if (ppNode->_left == parent)
{
ppNode->_left = subL; // parent原先的雙親節點接管subL,subL為這個子樹的根
}
else
{
ppNode->_right = subL;
}
subL->_parent = ppNode; // 更新subL的雙親指針
}
// 根據調整後的結構更新parent和subL的平衡因子
parent->_bf = subL->_bf = 0;
}
② 左單旋 - 新節點插入較高右子樹的最右側
將新的節點插入到了 parent 右孩子的右子樹上,導致的不平衡的情况。
引發左單旋的條件:
- 父親右邊高,左邊低,所以要讓父親往左旋。
- parent 的平衡因子為 2,parent 右孩子平衡因子為 1,觀察發現,平衡因子都是正數,說明是右邊高,也說明了==【引發旋轉的路徑是一條直線】==,所以我們要左旋操作。
左單旋操作:
- 讓 subR 的左子樹 subRL 成為 parent 的右子樹(因為 subRL 的左子樹根節點值大於30,小於60)
- 讓 parent 成為 subR 的左子樹(因為30小於60)
- 讓 subR 變成這個子樹的根
- 這一步操作前需要先判斷下:parent 是根節點,還是一個普通子樹
- 如果是根節點,則更新 subR 為新的根
- 如果是普通子樹(可能是某個節點的左子樹,也可能是右子樹,這裏需要判斷下),然後更新 subR 為這個子樹的根節點
- 根據樹的結構,更新 parent 和 subR 的平衡因子為0
在旋轉過程中,更新雙親指針的指向,有以下幾種情况需要考慮:
- subR 的左子樹 subRL 可能存在,也可能為空。(當不為空時才更新 subR 左子樹 subRL 的雙親指針指向)
- 旋轉完成後,subR 的雙親節點,可能是空,也可能是 parent 原先的父節點。(所以更新 subR 的雙親指針前需要判斷下)
代碼如下:
總的來說,就是依次調整 subRL、parent、subR 的比特置和雙親指針的指向。
// 左單旋
void treeRotateLeft(Node* parent)
{
// subR:父親的右孩子
// subRL:父親的右孩子的左孩子(大於父親,小於subR)
Node* subR = parent->_right;
Node* subRL = subR->_left;
// 1、讓subRL成為父親的右子樹
parent->_right = subRL;
// 如果subRL不為空
if (subRL)
{
subRL->_parent = parent; // 更新subRL雙親指針,指向parent
}
// 2、讓parent成為subR的左子樹
subR->_left = parent;
// 2.1、先記錄下parent的雙親節點
Node* ppNode = parent->_parent;
// 2.2、更新parent雙親指針的指向
parent->_parent = subR;
// 2.3、判斷parent是不是根節點
// 是根節點
if (parent == _root)
{
_root = subR; // subR為新的根
subR->_parent = nullptr; // subR雙親指針指向空
}
// 不是根節點,就是一個普通子樹
else
{
// 判斷parent原先是左孩子還是右孩子
if (ppNode->_left == parent)
{
ppNode->_left = subR; // parent原先的雙親節點接管subR,subR為這個子樹的根
}
else
{
ppNode->_right = subR;
}
subR->_parent = ppNode; // 更新subR的雙親指針
}
// 根據樹的結構,更新parent和subR的平衡因子
parent->_bf = subR->_bf = 0;
}
③ 左右雙旋 - 新節點插入較高左子樹的右側
將新的節點插入到了 parent 左孩子的右子樹上,導致的不平衡的情况。
這時我們需要的是先對 parent 的右孩子進行一次左旋,再對 parent 進行一次右旋。
這裏可以觀察到一個現象:
節點60的左右子樹被分走了,左子樹最終成了30的右子樹,右子樹最終成了90的左子樹。
下圖是 h = 0 的情况:
引發雙旋的條件:
- 引發旋轉的路徑是直線就是單旋,如果是折線就是雙旋
- parent 的平衡因子為 -2,parent 左孩子平衡因子為 1,觀察發現,平衡因子是一負一正,說明「左孩子右邊高」,「父親左邊高」,也說明了==【引發旋轉的路徑是一條折線】==,所以我們要先「對左孩子進行左旋操作」,再「對父親進行右旋操作」。
左右雙旋操作後,根據樹的結構,更新平衡因子時,需要注意:
插入新節點的比特置不同,經過左右雙旋後,得到樹的結構也會有所不同,平衡因子也會有所不同,有以下三種情况:
- 新節點插入到了「parent 左孩子的右子樹」的左邊
- 新節點插入到了「parent 左孩子的右子樹」的右邊
- 新節點就是「parent 左孩子的右孩子」
這裏可以觀察到一個現象,根據這個現象就很好推出旋轉後的平衡因子:
節點60的左右子樹被分走了,左子樹最終成了節點30的右子樹,右子樹最終成了節點90的左子樹。
代碼如下:
// 左右雙旋
void treeRotateLR(Node* parent)
{
Node* subL = parent->_left; // 記錄parent的左孩子
Node* subLR = subL->_right; // 記錄parent的左孩子的右孩子
// 旋轉之前,因為插入新節點的比特置不同,subLR的平衡因子可能是-1/0/1
int bf = subLR->_bf; // 記錄subLR的平衡因子
treeRotateLeft(parent->_left); // 先對parent的左孩子進行左單旋
treeRotateRight(parent); // 再對parent進行右單旋
// 旋轉完成之後,根據情况對其他節點的平衡因子進行調整
if (bf == -1)
{
parent->_bf = 1;
subL->_bf = 0;
subLR->_bf = 0;
}
else if (bf == 1)
{
parent->_bf = 0;
subL->_bf = -1;
subLR->_bf = 0;
}
else if (bf == 0)
{
parent->_bf = 0;
subL->_bf = 0;
subLR->_bf = 0;
}
else
{
assert(false);
}
}
④ 右左雙旋 - 新節點插入較高右子樹的左側
將新的節點插入到了 parent 右孩子的左子樹上,導致的不平衡的情况。
這時我們需要的是先對 parent 的右孩子進行一次右旋,再對 parent 進行一次左旋。
這是 h = 1 的情况:
引發雙旋的條件:
- 引發旋轉的路徑是直線就是單旋,如果是折線就是雙旋
- parent 的平衡因子為 2, parent 右孩子平衡因子為 -1,觀察發現,平衡因子是一正一負,說明「右孩子左邊高」,「父親右邊高」,也說明了==【引發旋轉的路徑是一條折線】==,所以我們要先「對右孩子進行右旋操作」,再「對父親進行左旋操作」。
左右雙旋操作後,根據樹的結構,更新平衡因子時,需要注意:
插入新節點的比特置不同,經過右左雙旋後,得到樹的結構也會有所不同,平衡因子也會有所不同,有以下三種情况:
- 新節點插入到了「parent 右孩子的左子樹」的左邊
- 新節點插入到了「parent 右孩子的左子樹」的右邊
- 新節點就是「parent 右孩子的左孩子」
這裏可以觀察到一個現象,根據這個現象就很好推出旋轉後的平衡因子:
節點60的左右子樹被分走了,左子樹 b 最終成了節點30的右子樹,右子樹 c 最終成了節點90的左子樹。
代碼如下:
// 右左雙旋
void treeRotateRL(Node* parent)
{
Node* subR = parent->_right; // 記錄parent的右孩子
Node* subRL = subR->_left; // 記錄parent的右孩子的左孩子
// 旋轉之前,因為插入新節點的比特置不同,subRL的平衡因子可能為-1/0/1
int bf = subRL->_bf; // 記錄subRL的平衡因子
treeRotateRight(parent->_right); // 先對parent的右孩子進行右單旋
treeRotateLeft(parent); // 再對parent進行左單選
// 旋轉完成之後,根據樹的結構對其他節點的平衡因子進行調整
if (bf == -1)
{
parent->_bf = 0;
subR->_bf = 1;
subRL->_bf = 0;
}
else if (bf == 1)
{
parent->_bf = -1;
subR->_bf = 0;
subRL->_bf = 0;
}
else if(bf == 0)
{
parent->_bf = 0;
subR->_bf = 0;
subRL->_bf = 0;
}
else
{
assert(false);
}
}
1.4 AVL樹的驗證
AVL樹是在二叉搜索樹的基礎上加入了平衡性的限制,因此要驗證AVL樹,可以分兩步:
- 驗證其是否為二叉搜索樹
如果中序遍曆可以得到一個有序的序列,就說明為二叉搜索樹。
- 驗證其是否為平衡樹
每個節點子樹高度差的絕對值不超過1
節點的平衡因子是否計算正確
(1)首先寫一個計算當前樹高度的函數
// 計算當前樹的高度
int Height(Node* root)
{
// 當前樹為空,則高度為0
if (root == nullptr)
return 0;
// 當前樹不為空,計算左右子樹的高度
int leftHeight = Height(root->_left);
int rightHeight = Height(root->_right);
// 當前樹的高度 = 左右子樹中高度最大的那個加1
return max(leftHeight, rightHeight) + 1;
}
(2)檢查AVL樹是否平衡,思路一:自頂向下的暴力解法
// 檢查AVL樹是否平衡,思路一
bool IsBalance1()
{
return _IsBalance1(_root);
}
bool _IsBalance1(Node* root)
{
// 當前樹為空,說明是平衡的
if (root == nullptr)
return true;
// 當前樹不為空,計算左右子樹的高度
int leftHeight = Height(root->_left);
int rightHeight = Height(root->_right);
if (rightHeight - leftHeight != root->_bf) // 檢查當前樹的平衡因子是否計算正確
{
cout << "平衡因子异常:" << root->_kv.first << endl;
}
// 左右子樹高度相减的絕對值小於2,說明當前樹是平衡的,則繼續往下判斷其它子樹
return abs(leftHeight - rightHeight) < 2
&& _IsBalance1(root->_left)
&& _IsBalance1(root->_right);
}
(3)檢查AVL樹是否平衡,思路二:自底向上的高效解法(動態規劃,前一個子問題的解,能够用於後一個問題求解)
// 檢查AVL樹是否平衡,思路二
bool IsBalance2()
{
return _IsBalance2(_root) != -1;
}
int _IsBalance2(Node* root)
{
// 先判斷當前樹的左、右子樹是否平衡,再判斷當前樹是否平衡
// 不平衡返回-1,平衡則返回當前樹的高度
// 當前樹為空,返回高度0
if (root == nullptr)
return 0;
// 當前樹不為空,分別計算左右子樹的高度
int leftHeight = _IsBalance2(root->_left);
int rightHeight = _IsBalance2(root->_right);
if (rightHeight - leftHeight != root->_bf) // 檢查當前樹的平衡因子是否計算正確
{
cout << "平衡因子异常:" << root->_kv.first << endl;
}
// 左子樹高度等於-1、右子樹高度等於-1、左右子樹高度差的絕對值大於1,說明當前樹不平衡
if (leftHeight == -1 || rightHeight == -1 || abs(leftHeight - rightHeight) > 1)
return -1;
// 運行到這裏來了,說明當前樹是平衡的,返回當前樹的高度
return max(leftHeight, rightHeight) + 1;
}
1.5 AVL樹 - 删除節點(了解)
因為AVL樹也是二叉搜索樹,可按照二叉搜索樹的方式將節點删除,然後再更新平衡因子,如果出現不平衡樹,進行旋轉。只不過與二叉搜索樹不同的是,AVL樹删除節點後的平衡因子更新,最差情况下一直要調整到根節點的比特置。
1.6 AVL樹的性能
AVL樹是一棵絕對平衡的二叉搜索樹,接近於完全二叉樹,其要求每個節點的左右子樹高度差的絕對值都不超過1,這樣可以保證查詢時高效的時間複雜度,即 O(log2N)。但是如果要對AVL樹做一些結構修改的操作,性能非常低下,比如:插入時要維護其絕對平衡,旋轉的次數比較多,更差的是在删除時,有可能一直要讓旋轉持續到根的比特置。因此:如果需要一種查詢高效且有序的數據結構,而且數據的個數為靜態的(即不會改變),可以考慮AVL樹,但一個結構經常修改,就不太適合。
边栏推荐
- [tcapulusdb knowledge base] [list table] example code of batch deleting data at specified location in the list
- Two ways to improve the writing efficiency of hard disk storage data
- 第一批00后下场求职:不要误读他们的“不一样”
- 静态查找表和静态查找表
- P1347 排序(topo)
- Swiftui component encyclopedia creating animated 3D card scrolling effects using Scrollview and geometryreader
- 【LeetCode】179. Maximum number
- 怎样能在小程序中实现视频通话及互动直播功能?
- bubble sort
- linux下的开源数据库是什么
猜你喜欢
Software project management 8.4 Software project quality plan

基于HAProxy实现网页动静分离

AI 视频云 VS 窄带高清,谁是视频时代的宠儿

选择排序法
![[machine learning] wuenda's machine learning assignment ex2 logistic regression matlab implementation](/img/eb/0d4caf0babbe14f51f4dbf1b9ae65d.png)
[machine learning] wuenda's machine learning assignment ex2 logistic regression matlab implementation

直接插入排序

在 KubeSphere 上部署 Apache Pulsar
![[greed] leetcode991 Broken Calculator](/img/6e/ce552b55899c6e8d3c37f524f99f82.png)
[greed] leetcode991 Broken Calculator

x64dbg 基本使用技巧

背景彩带动画插件ribbon.js
随机推荐
January 17, 2022: word rule II. Give you a pattern and a character
Pytorch---使用Pytorch的预训练模型实现四种天气分类问题
Swiftui component encyclopedia creating animated 3D card scrolling effects using Scrollview and geometryreader
redis 精讲系列介绍八 - 淘汰策略
What if the self incrementing IDs of online MySQL are exhausted?
Flutter怎么实现不同缩放动画效果
高效的远程办公经验 | 社区征文
QMainWindow
Software project management 8.4 Software project quality plan
页面导出excel的三种方式
JD cloud distributed database stardb won the "stability practice pioneer" of China Academy of information technology
P1363 幻象迷宫(dfs)
What is the difference between redistemplate and CacheManager operation redis
选择排序法
背景彩带动画插件ribbon.js
D overloading nested functions
元素的常用事件
SVG+JS智能家居监控网格布局
Preface
The tax software exits when it detects that it is a virtual machine. How to solve this problem?