当前位置:网站首页>【luogu P6656】【LOJ 173】【模板】Runs(字符串)(Lyndon 串)
【luogu P6656】【LOJ 173】【模板】Runs(字符串)(Lyndon 串)
2022-07-23 17:44:00 【SSL_TJH】
【模板】Runs
题目链接:luogu P6656 / LOJ 173
题目大意
给你一个字符串,要你求它所有的 Runs。
思路
本文也是参考着 command_block 大神的博客 进行学习的,只是书写一下自己的个人理解。
然后就开始讲了咯。
(文中许多东西建立在前面这篇文章的基础上,所以讲也不会再讲之前的内容)
定义
Run & Runs
一个三元组 r = ( l , r , p ) r=(l,r,p) r=(l,r,p) 是 r u n \rm run run 当且仅当:
字符串 s s s 中 l ∼ r l\sim r l∼r 形成的子串, p p p 是最小循环节,而且 2 p ⩽ r − l + 1 2p\leqslant r-l+1 2p⩽r−l+1。
而且这个串是不能延伸的,具体一点就是 s l − 1 ≠ s l + p − 1 , s r + 1 ≠ s r − p + 1 s_{l-1}\neq s_{l+p-1},s_{r+1}\neq s_{r-p+1} sl−1=sl+p−1,sr+1=sr−p+1。
然后一个字符串所有的 r u n \rm run run 就组成了 R u n s \rm Runs Runs。
一个 run 的指数是 e r = r − l + 1 p e_r=\dfrac{r-l+1}{p} er=pr−l+1
ρ r u n ( n ) ρ_{\rm run}(n) ρrun(n) 是长度为 n n n 的字符串至多有的 r u n \rm run run 的个数。
σ r u n ( n ) σ_{\rm run}(n) σrun(n) 是长度为 n n n 的字符串的 r u n \rm run run 的指数和的最大值。
Lyndon Root
这个东西一般是指一个 r u n \rm run run 的 Lyndon Root。
是一个在 r u n \rm run run 所在区间的子区间,而且长度为 p p p,还是 Lyndon Word。
意思其实就是说是 r u n \rm run run 的循环节的最小表示的那个。
然后不难看出对于任意一个 r r r 至少有一个 Lyndon Root,而且每一个之间其实是相等的,只是位置不同。
Run
为了方便书写,我们设 Lyndon Word 为 L y \rm Ly Ly,Lyndon Root 为 L y R \rm LyR LyR。
首先有个性质,就是两个周期相同为 p p p 的 run 的交的长度是 < p <p <p 的。
因为如果 > p >p >p 我们可以在交中选一个循环节扩展,就矛盾了。
(性质 1 1 1)
接着我们就要证明我们最重要的东西了:
ρ r u n ( n ) < n , σ r u n ( n ) ⩽ 3 n − 3 ρ_{\rm run}(n)<n,σ_{\rm run}(n)\leqslant 3n-3 ρrun(n)<n,σrun(n)⩽3n−3
首先我们之前有一个说那个比较大小可以重载的( < 0 , < 1 <_0,<_1 <0,<1),我们找找有关的性质。
然后因为有相反的,所有我们在前面比较完有一个空了的时候就要区别开来,所以我们会有一个占位符 $ \texttt{\textdollar} $,在 < 0 <_0 <0 里面我们让 $ \texttt{\textdollar} $ 字典序最小, < 1 <_1 <1 里面就是最大。
那我们就有这么一个小定义:
L y s , f ( i ) {\rm Ly}_{s,f}(i) Lys,f(i) 为 [ i , j ] [i,j] [i,j],其中 j j j 是 max { k ∣ s [ i , k ] \max\{k|s[i,k] max{ k∣s[i,k] 是关于 < f <_f <f 的 L y } \rm Ly \} Ly}
也就是在 < f <_f <f 意义下,起始位置为 i i i 的最长的 L y \rm Ly Ly 子串。
然后有一个事情就是正反两个字典序只能有一个会找到长度大于 1 1 1 的 L y \rm Ly Ly。
形式化就是:只有恰好一个 f ∈ { 0 , 1 } f\in\{0,1\} f∈{ 0,1} 使得 L y s , f ( i ) = [ i , i ] , L y s , 1 − f ( i ) = [ i , j ] ( j > i ) {\rm Ly}_{s,f}(i)=[i,i],{\rm Ly}_{s,1-f}(i)=[i,j](j>i) Lys,f(i)=[i,i],Lys,1−f(i)=[i,j](j>i)
你就看后面第一个跟 s i s_i si 不同的字符(因为有占位符所以必定存在),如果是在这个意义下是小于那就不能加上,所以只有自己的位置,否则至少也有那个不同的位置是可以作为 L y {\rm Ly} Ly 的。
(性质 2 2 2)
然后就是对于一个 r u n {\rm run} run,设为 r = ( l , r , p ) r=(l,r,p) r=(l,r,p),找到 f ∈ { 0 , 1 } f\in\{0,1\} f∈{ 0,1} 使得 s r + 1 < f s r − p + 1 s_{r+1}<_fs_{r-p+1} sr+1<fsr−p+1,那么 r r r 所有关于 < f <_f <f 的 L y R {\rm LyR} LyR(设为 [ i , j ] [i,j] [i,j]) 都跟 L y s , f ( i ) {\rm Ly}_{s,f}(i) Lys,f(i) 相等。
因为是 L y {\rm Ly} Ly 循环节嘛,我们可以表示为 u c u ′ u^cu' ucu′(不用找 L y {\rm Ly} Ly 循环节),其中 u ′ u' u′ 是 u u u 严格前缀(就是不能等于)
你会发现它长得很像 Duval 算法里面的那个形式。
然后如果你用 1 − f 1-f 1−f,你会根据性质 2 2 2 发现都是一个字符,没有意义。
我们也发现这个 f f f 它这样在 r u n {\rm run} run 中有特殊的地方,于是我们把这个 < f <_f <f 记为 r r r 的正序。
(性质 3 3 3)
然后再设一个 L y R s ( r ) {\rm LyRs}(r) LyRs(r) 表示 r r r 所有正序的 L y R {\rm LyR} LyR,除去 l l l 开头的(如果有)。
然后我们会发现 ∣ L y R s ( r ) ∣ ⩾ ⌊ e r − 1 ⌋ ⩾ 1 |{\rm LyRs}(r)|\geqslant \left\lfloor e_r-1\right\rfloor\geqslant 1 ∣LyRs(r)∣⩾⌊er−1⌋⩾1
其实挺显然的?
首先第二个跟第三个那肯定没问题,毕竟你 2 p ≤ l e n 2p\leq len 2p≤len,那肯定 e r ⩾ 2 e_r\geqslant 2 er⩾2 了。
然后是第一个跟第二个,那 ∣ L y R s ( r ) ∣ |{\rm LyRs}(r)| ∣LyRs(r)∣ 就是看有多少个循环节,会发现跟 e r e_r er 差不多。
但是由于可能会除去一个 l l l 开头的,所以要减一,而且可能跑不满一个新的循环节,所以是下取整。
(性质 4 4 4)
对于两个不同的 r u n {\rm run} run( r = ( l , r , p ) , r ′ = ( l ′ , r ′ , p ′ ) r=(l,r,p),r'=(l',r',p') r=(l,r,p),r′=(l′,r′,p′)),它们的 L y R s {\rm LyRs} LyRs 的左端点集合不会有交。
设左端点集合为 B e g ( x ) {\rm Beg}(x) Beg(x),就是 B e g ( L y R s ( r ) ) ∩ B e g ( L y R s ( r ′ ) ) = ∅ {\rm Beg}({\rm LyRs}(r))∩{\rm Beg}({\rm LyRs}(r'))=\varnothing Beg(LyRs(r))∩Beg(LyRs(r′))=∅。
考虑反证法,设存在且是位置 i i i,那两个 L y R {\rm LyR} LyR 设是 [ i , j ] , [ i , j ′ ] [i,j],[i,j'] [i,j],[i,j′]。
然后设 < f <_f <f 是 r r r 的正序,然后你会发现 L y s , f ( i ) {\rm Ly}_{s,f}(i) Lys,f(i) 就是两个的表示?
但是显然两个的这个值应该要不一样啊,不然就是同一个 r u n {\rm run} run 了。
那只能是一个正序一个反序,所以另一个就是 L y s , 1 − f ( i ) {\rm Ly}_{s,1-f}(i) Lys,1−f(i)。
那必然有一个 [ i , i ] [i,i] [i,i],设 j = i j=i j=i,就有 j ′ > i j'>i j′>i。(性质 2 2 2)
那因为 [ i , j ′ ] [i,j'] [i,j′] 是 L y {\rm Ly} Ly,所以自然 s i ≠ s j ′ s_i\neq s_{j'} si=sj′,再从性质 3 3 3 会有 r r r 的循环节是 p = ∣ [ i , i ] ∣ = 1 p=|[i,i]|=1 p=∣[i,i]∣=1, r ′ r' r′ 的循环节就是 p ′ = ∣ [ i , j ′ ] ∣ = j − i + 1 p'=|[i,j']|=j-i+1 p′=∣[i,j′]∣=j−i+1。
那周期性一下: s i = s i − 1 = s i − 1 + ( j − i + 1 ) = s j ′ s_i=s_{i-1}=s_{i-1+(j-i+1)}=s_{j'} si=si−1=si−1+(j−i+1)=sj′,与 s i = s j ′ s_i=s_{j'} si=sj′ 矛盾。
所以就证好了。
(性质 5 5 5)
不难通过性质 5 5 5 发现,最多每个左端点都被占了,再把 l l l 给去掉,所以我们可以证明:
ρ r u n ( n ) < n ρ_{\rm run}(n)<n ρrun(n)<n
再看看什么没用上,性质 4 4 4。
不难看出用到的是 ∣ L y R s ( r ) ∣ ⩾ ⌊ e r − 1 ⌋ |{\rm LyRs}(r)|\geqslant \left\lfloor e_r-1\right\rfloor ∣LyRs(r)∣⩾⌊er−1⌋。
下取整不行换一下 ∣ L y R s ( r ) ∣ ⩾ ⌊ e r − 1 ⌋ ⩾ e r − 2 |{\rm LyRs}(r)|\geqslant \left\lfloor e_r-1\right\rfloor\geqslant e_r-2 ∣LyRs(r)∣⩾⌊er−1⌋⩾er−2
推广到所有 r u n {\rm run} run: ∑ r ∈ r u n s ( s ) e r − 2 ⩽ ∑ r ∈ r u n s ( s ) ∣ L y R s ( r ) ∣ ⩽ n − 1 \sum\limits_{r\in {\rm runs}(s)}e_r-2\leqslant \sum\limits_{r\in {\rm runs}(s)}|{\rm LyRs}(r)|\leqslant n-1 r∈runs(s)∑er−2⩽r∈runs(s)∑∣LyRs(r)∣⩽n−1
再结合一下 ∣ r u n s ( s ) ∣ ⩽ n − 1 |{\rm runs(s)}|\leqslant n-1 ∣runs(s)∣⩽n−1,把 − 2 -2 −2 提出来:
( ∑ r ∈ r u n s ( s ) e r ) − 2 ( n − 1 ) ⩽ n − 1 (\sum\limits_{r\in {\rm runs}(s)}e_r)-2(n-1)\leqslant n-1 (r∈runs(s)∑er)−2(n−1)⩽n−1
σ r u n ( n ) − 2 n + 2 ⩽ n − 1 σ_{\rm run}(n)-2n+2\leqslant n-1 σrun(n)−2n+2⩽n−1
σ r u n ( n ) ⩽ 3 n − 3 σ_{\rm run}(n)\leqslant 3n-3 σrun(n)⩽3n−3
搞定!
(性质 6 6 6)
Ex
ρ r u n , k ( n ) < n k − 1 ρ_{ {\rm run},k}(n)<\dfrac{n}{k-1} ρrun,k(n)<k−1n, ρ r u n , k ρ_{ {\rm run},k} ρrun,k 表示 e r e_r er 达到 k k k 的 r u n \rm run run 的个数。
挺显然的,就结合一下占位的想法看看就知道了。
计算
假设我们直接暴力找:
就是枚举周期 p p p,然后在串中撒点(均匀撒),然后鸽笼(也许不需要)一下就知道一个大小为 p p p 的 r u n \rm run run 一定会穿过至少两个点。
那就相邻两个点之间向前向后求 L C P \rm LCP LCP,如果覆盖范围能连接起来,就找到了一个。
当然你可以用性质 1 1 1 小小剪枝。
而且你会发现你枚举的周期不一定是最小周期,所以我们得排序,然后去重一下。
然后如果二分+Hash搞就是 n log 2 n n\log^2n nlog2n,后缀数组搞就是 n log n n\log n nlogn。
感觉不优。
在介绍新的求法之前,不妨看看这么一个问题,如何快速求所有 L y s ( i ) {\rm Ly}_s(i) Lys(i)。
考虑从那个合并的角度来看,从右往左扫,每次加进去一个字符(然后你用一个栈维护前面的 L y {\rm Ly} Ly)。
然后不停的查看是否能合并,然后这个地方比大小我们就先二分+Hash找到不同的位置,然后用当前的 f f f 判断一下即可。
考虑用上一些性质,就我们可以从性质 2 2 2 发现,一个 r u n \rm run run 含有的 L y {\rm Ly} Ly 循环节是某个字典序下某个后缀最长 L y {\rm Ly} Ly 前缀。
而且两个不同的 r u n {\rm run} run 的循环节肯定不同。
我们考虑直接枚举循环节,直接前后求 L C P {\rm LCP} LCP,这样循环节是 O ( n ) O(n) O(n) 的。
具体一点就是枚举 f , l f,l f,l,然后由于我们求出了所有的 L y s ( i ) {\rm Ly}_s(i) Lys(i),我们就 L C P {\rm LCP} LCP 得到扩展,然后判一下是否能相交即可。
然后也是要去重。
然后由于后缀数组预处理要 n log n n\log n nlogn,不如使用二分+hash,好写一点。
这里我们就是使用了 L y {\rm Ly} Ly 串构造最小循环节,可以说是一种映射,所以就把复杂度降到了 O ( n ) O(n) O(n)。
代码
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define ull unsigned long long
#define di 131
using namespace std;
const int N = 1e6 + 100;
struct node {
int l, r, p;
}ans[N];
char s[N];
int n, ly[N], sta[N], m, ans_num;
ull mi[N], hsh[N];
void Init() {
mi[0] = 1;
for (int i = 1; i <= n; i++) {
mi[i] = mi[i - 1] * di;
hsh[i] = hsh[i - 1] * di + s[i] - 'a';
}
}
ull get(int l, int r) {
return hsh[r] - hsh[l - 1] * mi[r - l + 1];
}
int getl(int x, int y) {
int l = 0, r = min(x, y), re = 0;
while (l <= r) {
int mid = (l + r) >> 1;
if (get(x - mid + 1, x) == get(y - mid + 1, y)) re = mid, l = mid + 1;
else r = mid - 1;
}
return re;
}
int getr(int x, int y) {
int l = 0, r = min(n - x + 1, n - y + 1), re = 0;
while (l <= r) {
int mid = (l + r) >> 1;
if (get(x, x + mid - 1) == get(y, y + mid - 1)) re = mid, l = mid + 1;
else r = mid - 1;
}
return re;
}
bool cmpS(int x, int y) {
int sz = getr(x, y);
return s[x + sz] < s[y + sz];
}
void Lyndon(bool op) {
ly[n] = n;
sta[0] = 0; sta[++sta[0]] = n + 1; sta[++sta[0]] = n;
for (int i = n - 1; i >= 1; i--) {
while (sta[0] > 1 && cmpS(i, sta[sta[0]]) == op) sta[0]--;
sta[++sta[0]] = i;
ly[i] = sta[sta[0] - 1] - 1;
}
}
void slove(int x, int y) {
int l = getl(x, y), r = getr(x, y);
if (l + r >= y - x + 1) {
ans[++m] = (node){
x - l + 1, y + r - 1, y - x};
}
}
bool cmp(node x, node y) {
if (x.l != y.l) return x.l < y.l;
if (x.r != y.r) return x.r < y.r;
return x.p > y.p;
}
int main() {
scanf("%s", s + 1); n = strlen(s + 1);
Init();
for (int op = 0; op <= 1; op++) {
Lyndon(op);
for (int i = 1; i < n; i++)
slove(i, ly[i] + 1);
}
sort(ans + 1, ans + m + 1, cmp);
for (int i = 1; i <= m; i++) {
if (ans[i].l == ans[i - 1].l && ans[i].r == ans[i - 1].r) continue;
ans_num++;
}
printf("%d\n", ans_num);
for (int i = 1; i <= m; i++) {
if (ans[i].l == ans[i - 1].l && ans[i].r == ans[i - 1].r) continue;
printf("%d %d %d\n", ans[i].l, ans[i].r, ans[i].p);
}
return 0;
}
边栏推荐
- C语言小项目 -- 通讯录(静态版+动态版+文件版)
- FPGA flash reading and writing based on SPI
- 正则化不同导致的tuple错误
- .net core implements background tasks (scheduled tasks) longbow Tasks component (III)
- (CVPR-2022)BiCnet
- @JPA annotation in entity
- AE 教程,如何在 After Effects 中对 Illustrator 分图层文档进行动画绘制?
- A preliminary study of the relationship between combinatorial mathematics and DP, and the derivation of resettable combinatorial formulas
- [Nuxt 3] (九)服务器路由
- 三维点云课程(七)——特征点描述
猜你喜欢
Using FRP to achieve intranet penetration

进程调度的基本过程

【开发经验】开发项目踩坑集合【持续更新】
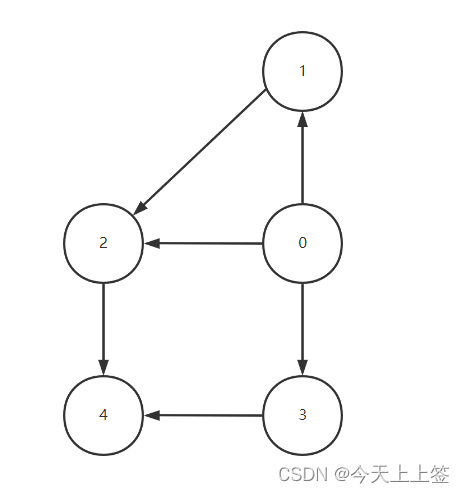
有向图之求两点之间所有路径

J9数字论:数字行业的FOMO现象我们应该怎么克服?

lendingclub贷款状态loan status业务详解-current,charge off,issued,Fully Paid,grace period

Conception de l'interface UART basée sur la FPGA

【leetcode天梯】链表 · 022 链表中倒数第k个节点
![[shutter -- layout] linear layout (row and column)](/img/0e/df0f4bce73dd9785cc843adaf371d0.png)
[shutter -- layout] linear layout (row and column)

AE tutorial, how to animate illustrator layered documents in after effects?
随机推荐
Labyrinth DP integration
elk笔记25--快速体验APM
【leetcode天梯】链表 · 203 移除链表元素
Shell
Using FRP to achieve intranet penetration
Implementation of IIC protocol with FPGA (I) IIC bus protocol
有向图之求两点之间所有路径
How can mysqldump export content without comments?
软件测试岗位就业竞争压力大,985毕业的“打工人“同样存在苦不堪言
[shutter -- layout] flexible layout (flex and expanded)
树莓派ssh登录
R语言使用quantile函数计算向量数据或者dataframe指定数据列的分位数(百分位数)
Testing scheme of granite dielectric constant by network
GPS北斗时钟服务器(NTP网络时钟系统)施工部署方案
国外芯片,为什么有中文资料和网页?
去中心化存储面临的挑战
入门数据库days1
在Hyper-V中手动将.avhd合并到.vhd
Exch:POP3 和 IMAP4 操作指南
.Net CLR R2R编译的原理简析