当前位置:网站首页>A preliminary study of the relationship between combinatorial mathematics and DP, and the derivation of resettable combinatorial formulas
A preliminary study of the relationship between combinatorial mathematics and DP, and the derivation of resettable combinatorial formulas
2022-07-23 19:25:00 【lovesickman】
4002. Construct an array ( Reveals DP The essence of is combinatorics )
Now you need to construct a pair of arrays ( a , b ) (a,b) (a,b), requirement :
- Array a a a And an array b b b The length of each of them is m m m.
- The value range of the elements in both arrays is [ 1 , n ] [1,n] [1,n].
- ∀ i ∈ [ 1 , m ] ∀i∈[1,m] ∀i∈[1,m], a i ≤ b i ai≤bi ai≤bi.
- Array a a a Elements in are not strictly monotonically increasing .
- Array b b b Elements in are not strictly monotonically decreasing .
Excuse me, , How many pairs of arrays that meet the conditions can be constructed ?
Output pair 1 0 9 + 7 10^9+7 109+7 The result after taking the mold .
At first glance, there are many conditions , It's hard .
Method : A combination of numbers and shapes , Multiplication principle ( Consider step by step )
Just draw casually on the paper a a a and b b b You can find that the problem can be transformed into :
- from n n n In number ( Each number can be selected repeatedly ) choose 2 ∗ m 2*m 2∗m Number , Arrange these numbers , The big half is for b b b , Give the other half a a a .
- analysis a a a Medium m m m Number , How many distribution schemes are there ?
answer 2 : Find the given m m m After the number is determined , The plan is the only .
So the problem is equivalent to 1 Number of alternatives ( Classical reconfigurable set combinatorial problem ), The answer is C ( 2 m + n − 1 , n − 1 ) C(2m+n-1,n-1) C(2m+n−1,n−1)
Mathematical derivation :( Ideas , It is known that C ( n , m ) C(n,m) C(n,m) From n n n individual Different Take from the number of m m m Number of projects ).
The following is the template thinking routine in Mathematics :
- set up x i x_i xi It means the first one i i i How many to take . Yes ∑ i = 1 n x i = 2 ∗ m , x i ≥ 0 \sum_{i=1}^{n} x_i =2*m,x_i \ge0 ∑i=1nxi=2∗m,xi≥0
- set up x i ′ = x i + 1 x'_i = x_i +1 xi′=xi+1 Yes ∑ i = 1 n x i = 2 ∗ m + n , x i > 0 \sum_{i=1}^{n} x_i =2*m+n,x_i > 0 ∑i=1nxi=2∗m+n,xi>0
- The problem turns into a given 2 ∗ m + n 2*m+n 2∗m+n A little ball , use n − 1 n-1 n−1 A partition divides all the small balls into n n n part , The number of balls in each part must Greater than 0 0 0 . because x i > 0 x_i>0 xi>0 , So the clapboard has 2 ∗ m + n − 1 2*m+n-1 2∗m+n−1 A place , And because each partition is different , So it can be used C ( 2 m + n − 1 , n − 1 ) C(2m+n-1,n-1) C(2m+n−1,n−1) Express . Obtain evidence .
One small TRICK C ( 2 m + n − 1 , n − 1 ) C(2m+n-1,n-1) C(2m+n−1,n−1) = C ( 2 m + n − 1 , 2 m ) C(2m+n-1,2m) C(2m+n−1,2m) Which data range is small, which one is used
How to find the combination number ? C ( n , m ) = C ( n − 1 , m − 1 ) + C ( n − 1 , m ) C(n,m) = C(n-1,m-1) + C(n-1,m) C(n,m)=C(n−1,m−1)+C(n−1,m) Isn't that what 0/1 The derivation of knapsack ?
therefore : C ( 2 m + n − 1 , n − 1 ) C(2m+n-1,n-1) C(2m+n−1,n−1) It can be used 0 / 1 0/1 0/1 knapsack . 2 m + n − 1 2m+n-1 2m+n−1 It's the volume of the backpack , The volume of each element is 1 1 1 .
original DP The number of schemes can be calculated because DP The underlying logic of is combinatorics , The principle of multiplication and addition in combinatorics can solve the number of schemes .
So an obvious idea , Is it possible to use complete knapsack directly to find the number of schemes in a re set ? The answer is obvious !
The following is the code of two knapsacks seeking the same problem .
0/1 knapsack
f[0]=1;
for(int i=1;i<=2*m+n-1;i++){
for(int j=2*m;j>=1;j--){
f[j]= ((f[j] + f[j-1]) + M )%M;
}
}
cout<<f[2*m]<<endl;
Completely backpack
f[0]=1;
for(int i=1;i<=n;i++){
for(int j=1;j<=2*m;j++){
f[j]= ((f[j] + f[j-1]) + M )%M;
}
}
cout<<f[2*m]<<endl;
边栏推荐
- 从txt中读取数据转成yolo格式数据
- H7-TOOL的I2C接口方式脱机烧录操作方法,已经发布(2022-07-16)
- 基于FPGA的UART接口设计
- mBio | 海洋所孙超岷组在深海原位验证了微生物介导的单质硫形成新通路
- Read data from txt and convert it to Yolo format data
- canvas绘制文本和清除绘制
- Perl语言简述
- 【leetcode天梯】链表 · 206 反转链表
- FPGA实现IIC协议(二)之IIC总线的FPGA实现(单次读写驱动)
- It's too strong. An annotation handles the data desensitization returned by the interface
猜你喜欢
[paper reading] gettext: trajectory flow map enhanced transformer for next POI recommendation
![[C language] program environment and preprocessing](/img/5c/7f14c73e075a54a11d7ff44907c30d.jpg)
[C language] program environment and preprocessing

(CVPR-2022)BiCnet

界面设计四大原则

多线程&高并发(全网最新:面试题+导图+笔记)面试手稳心不慌
![[shutter -- layout] flexible layout (flex and expanded)](/img/03/0f07a56487f8e91045f9e893e9f96c.png)
[shutter -- layout] flexible layout (flex and expanded)

FPGA基于spi的flash读写
ES6其他语法及扩展语法总结
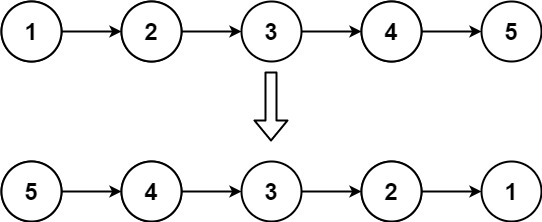
【leetcode天梯】链表 · 206 反转链表

Why are there Chinese materials and web pages for foreign chips?
随机推荐
Technical scheme of face recognition system
Fragment
EmguCV 常用函数功能说明「建议收藏」
FPGA实现IIC协议(二)之IIC总线的FPGA实现(单次读写驱动)
There is great competition pressure for software testing jobs, and the "migrant workers" who graduated from 985 also suffer
FPGA基于spi的flash读写
识别引擎ocropy-&gt;ocropy2-&gt;OCRopus3总结
Figure learning summary
Three ways to realize multithreading
What is the difference between preamplifier and power amplifier?
Ros2 self study notes: rviz visualization tool
Digital security giant entrust revealed that it was attacked by blackmail software gangs in June
【C语言】程序环境和预处理
Terminal command (all)
Time2Vec 的理解与简单实现
Learn and understand Architecture Design from business development
Tcl脚本语言基础(2)
基于FPGA的UART接口设计
SQL 语句练习
J9数字论:数字行业的FOMO现象我们应该怎么克服?
![[paper reading] gettext: trajectory flow map enhanced transformer for next POI recommendation](/img/8e/74cf3dc83f82dc1682125cb23f220a)