[principles of database system] Chapter 5 algebra and logic query language: package, extension operator, relational logic, relational algebra and datalog

The fifth chapter Algebraic and logical query language

5.1 package Multiset

The definition of package

• Definition ： That is, multiple sets , Multiset. The same tuple can appear multiple times in a relationship .

• Advantages of using packages ：

  • Improve the efficiency of parallel operation and projection operation .
  • To aggregate (SUM, COUNT etc. ) Useful （ Aggregate operations You can't Use the collection method , There will be logical errors ）.

---

Relationship operations on packages

• All operations on the package allow tuples to repeat before and after the operation .

• matters needing attention ：

  • aggregate Package operation on
    If for two sets R、S Perform packet based intersection and difference operations , The result is the same as that of set operation .

  • Because there are no duplicate tuples in the two relationships that are processed objects ,

    So there is still no duplicate tuple in the result after crossing or subtracting

    But for two sets R and S, Conduct Package based merging , The result of its operation may no longer be a set .

    • Be careful ： See clearly （ Answer the questions ）/ Statement （ Issue ） Is it package mode or collection mode

• On the algebraic laws of packets

  • Commutative law ：S ∪ R = R ∪ S.

• Relationship operations on packages ：

  • Package and 、 hand over 、 Bad

    set up R and S It's a bag , If tuple t stay R and S Appear in m Secondary sum n Time （ there m and n It can be 0）, be ：

    • R ∪ S Package and operation results ： Tuples t appear m+n Time ;
    • R ∩ S In the results of the outsourcing operation ： Tuples t appear min (m, n) Time ;
    • R - S The package difference operation result of ： Tuples t appear max(0, m-n) Time .

  • Projection operation of package

    It is basically consistent with the set projection , But there's no need to weigh it again .

  • Package selection

  • Cartesian product of packages
    
    

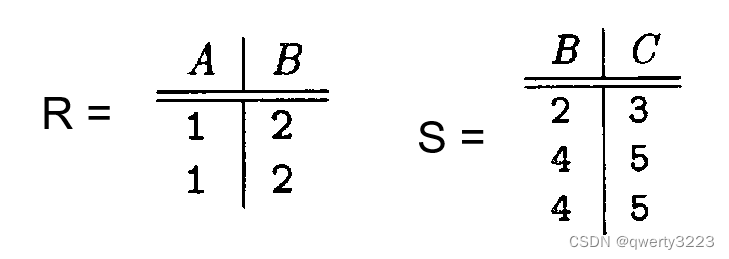
  • Connection of packages

    • Natural join

      

    • θ Connect

      

5.2 Extended operators of relational algebra

1. Eliminate duplicate $\delta (R)$
   Clear the duplicate elements in the package

   ---

2. Aggregate operation ($\text{SUM, AVG, MAX|MIN, COUNT}$)
   Count some tuples independently of other tuples in the same relationship 、 For maximum 、 minimum value 、 Average value and other operations

   • SUM Used to generate a column sum , What you get is a numerical value ;
   • AVG Used to generate a column of averages , The result is also a numerical value ;
   • MAX and MIN When used for numeric value columns , The resulting values are the largest and smallest values in this column ; When applied to character columns, the result is The largest and smallest of the lexicographic order ;
   • COUNT Generate “ value ” Number of ( It doesn't necessarily mean different values ). Again ,COUNT When applied to any attribute of a relationship , What is produced is the number of tuples of this relationship , Include duplicate tuples .

   ---

3. grouping ${\gamma }_L(R)$
   Group tuples on one or more attributes according to their values

   • application $\gamma$ An attribute of the relationship of operations ,R Use this attribute to group , It is called grouping attribute ;

     • for example ： chart 5-4 ${\gamma }_{studioname}(Movies)$

       	studioName
       	Disney
       	Disney
       	MGM
       	MGM

   • Applied to an attribute of the relationship Aggregation operator , You can use arrows to name the clustered attribute column ;

     • for example ：${\gamma }_{studioname,SUM(length)\to sumOfLength}(Movies)$

       studioName	sumOfLength
       Disney	12345
       MGM	54321

   • Examples of applications

     example 5.23 To the relationship StarsIn( title, year, starName), Check the movie stars who have acted in at least three films , And the earliest years they appeared in the film .

     
     

   ---

4. Sort ${\tau }_L(R)$
   Sort tuples of relationships according to one or more attributes .

   • expression ${\tau }_L(R)$, among R It's the relationship ,L yes R List of some attributes in . This expression represents the relationship R Of itself , Only all tuples in the result are pressed L To sort .
   • set up L By $A_1,A_2,\dots ,A_n$ form , that R First press $A_1$ Value ordering for , about $A_1$ Tuples with equal attributes press $A_2$ Value ordering for , By analogy .

   ---

5. Extended projection ${\pi }_L(R)$

   • Extended projection is to add some calculation operations as projection list on the basis of projection ;
   • The projection list can be ：
     • Relationship R A property of ;
     • Form like x→y The expression of ： take R Properties in x Rename it to y;
     • Form like E→z The expression of , among E It's about R Properties of 、 Constant 、 Arithmetic operator or string operator expression ,z Is an expression E The new name of the attribute of the calculation result .

   ---

6. External connection operation $*,*,*$
   Variant of join operation , The emergence of floating tuples

   • Definition of outer connection

     First calculate two relationships R and S The natural connection of ,

     And then put it from R or S Floating tuples of are added , use null The representation symbols of complement those attributes that do not have values in the result tuple .

   • Different variants of outer connection

     

     example ：

     

5.3 Relational logic

Datalog Language

• Datalog Language use if-then Rules to represent queries , That is, you can infer the query result through the combination of some tuples in the known relationship .

• Datalog Language consists of two basic atoms , namely Relational atoms and Arithmetic atom , Composed of atoms according to certain rules Datalog Query statement .

  • stay Datalog In language , The relationship passes through “ The predicate ” To express , Each predicate has a fixed number of parameters , Written as $P(x_1,x_2,\dots ,x_n)$, In essence, a predicate is a function that returns a Boolean value .

    • If R Is included n Attributes $a_1,a_2,\dots ,a_n$ The relationship between ,

      So when tuples $(t_1,t_2,\dots ,t_n)$ In relation R in , be $R(t_1,t_2,\dots ,t_n)$ It's true , Otherwise it is false .

    • Besides , You can use variables as arguments to predicates .

      example ：

      A	B
      1	2
      3	4

      For example, if you define R(x,y), Then when x=1 And y=2, perhaps x=3 And y=4 when ,R It's true , Otherwise it is false .

      If defined R(1,z), Then when z=2 when ,R It's true , Otherwise it is false .

The basic structure

• Arithmetic atom

  Comparison of two arithmetic expressions , The value is Boolean .

  $x<y$

  $x+1>y+5\times z$

• Extended predicates and connotative predicates

  • Extended predicates (EDB)：

    If the relation referred to by the predicate Stored in a database in , Call this predicate Extended predicates (EDB), Corresponding to operands in relational algebraic expressions .

  • Connotative predicate (IDB)：

    When the relationship referred to by the predicate is Through one or more Datalog The rule calculates Of , Call the predicate Connotative predicate , Corresponds to the relationship calculated using relational algebraic expressions .

The rules

General rules

• The rule is Datalog A specification in language that describes the association between atoms , It includes the following three components ：

  1. A relational atom called the head ;
  2. Left arrow symbol ←, pronounce as if;
  3. Main part , It consists of one or more atoms called sub targets .

• The sub target can be either a relational atom , It can also be arithmetic atom .

  Logical operators are used between sub goals AND Connect , And there can be NOT Negation operator .
  for example ：$LongMovie(t,y)\leftarrow Movies(t,y,l,g,s,p)ANDl\ge 100$

• The goal of the rules ： Make the head relation atom true .

Safety rules

• Because relationship instances are always limited , Therefore, the head relationship guaranteed by rules is also limited .

  • Each is in the rule Variables that appear anywhere Must appear in Some non negative relational sub goals of the subject in .

  • In especial Anything in the rule header 、 Negative relationship sub goal 、 Variables that appear in arithmetic sub goals , Must also appear in The non negative relationship sub goal of the subject in .

  • example ：

    Examples of safety violations ： P(x,y)←Q(x,z) AND NOT R(w,x,z) AND x<y

---

5.4 Relational algebra and Datalog

Set operations -> Datalog The rules

Intersection operation

• You can use one Datalog Rules to show

• Because the intersection operation involves two relations , So in Datalog In the rules , Have sub goals corresponding to two relationships ;

• In the rules , The corresponding parameters use the same variables .

• example ：

  hypothesis R and S The pattern of the relationship is R(A,B,C) and S(A,B,C),

  be R∩S Rules can be used :
  I(a, b, c) ← R(a, b, c) AND S(a, b, c)

Union operation

• Each rule corresponds to a relation in union operation , And the heads of the two rules have the same IDB The predicate ;

  The parameters of the head are exactly the same as those in each sub target .

• example ：

  hypothesis R and S The pattern of the relationship is R(A,B,C) and S(A,B,C),
  be R ∪ S Rules can be used :
  U(x, y, z) ← R(x, y, z)
  U(x, y, z) ← S(x, y, z) { or U(a, b, c) ← S(a, b, c)}

• Be careful ：

  Variable names are local to rules , namely Each rule is calculated independently , And provide tuples to its header relationship , It has nothing to do with other rules , Therefore, variable names are rule independent .

Subtraction operation

• You can use a rule with negate subgoals to calculate

  • That is, if you calculate U-V, The non negative subgoal is a predicate U, The inverse subgoal is a predicate V;
  • In this rule , The sub target and header have the same variables for the corresponding parameters .

• example ：

  hypothesis R and S The pattern of the relationship is R(A,B,C) and S(A,B,C),

  be R-S Rules can be used :
  D(x, y, z) ← R(x, y, z) AND NOT S(x, y, z)

Projection operation

• Use a rule with a single sub goal , The parameters of this sub goal are different variables , Each variable represents an attribute of the relationship ;

• The head is an atom with parameters , Its parameters correspond to the attributes of the projection list in the desired order .

• example ：

  example 5.25 The relationship Movies (title, year, length, genre, studioName, producerC#) Project to the first three attributes ：
  P(t, y, l) ← Movies(t, y, l, g, s, p)

Select operation

• If the selection condition is one or more arithmetic comparison expressions AND operation , You can create a with the following sub goals Datalog The rules ：

  • A relationship sub goal , Corresponding to the relationship in which it is selected . Each component of the relationship sub goal has different variables , And each component corresponds to an attribute of the relationship ;
  • Multiple arithmetic sub goals , Each arithmetic sub target corresponds to a comparison operation of the selection condition . Use the corresponding variables in the arithmetic sub goal , And keep consistent with the variables established in the relationship sub goal .

• example ：

  S(t,y,l,g,s,p) ← Movies(t,y,l,g,s,p) AND l≥ 100 AND s=‘Fox’

The cartesian product

• R×S You can use a single Datalog Rules to show
  • The rule contains two sub goals corresponding to R and S, The two sub goals set different variables corresponding to attributes .
  • Head IDB Predicates contain parameters that appear in all sub targets ,R The variables in the sub goals are listed in S In front of the variable .
    p(a,b,c,x,y,z) ← R(a,b,c) AND S(x,y,z)

Join operation

• Natural join （$R\bowtie S$）

  • Use an approximate Cartesian product Datalog Rules to show , The difference lies in R and S The public attribute column of uses the same variable , Otherwise, use different variables .

  • The rule header is a IDB The predicate , Every variable of it appears once .

  • example ：

    hypothesis R and S The pattern of the relationship is R(A,B) and S(B,C,D),

    Then natural connection $R\bowtie S$ You can use rules
    J(a,b,c,d) ← R(a,b) AND S(b,c,d)

• θ Connect

  • First transform the Cartesian product , Then transform the selection conditions .

Multiple operation

• The steps of simulating multiple operations are as follows ：

  • Draw the expression tree of relational algebra ;

  • The leaf nodes of the expression tree are represented by the corresponding extended predicates EDB Express ;

  • Create a for each internal node of the expression tree IDB The predicate .IDB One or more rules of the predicate correspond to the operators to be used on the tree nodes .

  • The predicate relationship associated with the root of the expression tree corresponds to the query result .

  • example ：

    

---

package -> Datalog The rules

• Relational algebra and Datalog Rules can be applied to package operations .

• take Datalog When rules are applied to packages , The operation steps are as follows ：

  • First step , Perform packet connection operation on the corresponding relationship of different sub targets ;

  • The second step , According to the content contained in the arithmetic sub goal , Perform packet selection operation on the result of connection operation ;

  • The third step , Perform packet projection operation on the selection result according to the relationship of rule headers .

  • example ：

    seek ${\pi }_{x,z}(R(x,y)\bowtie S(y,z))$
    H(x,z) ← R(x,y) AND S(y,z)

Datalog Comparison between rules and relational algebra

• Every operation of basic relational algebra can be used Datalog Query expression , But the operations of grouping and aggregation in extended relational algebra cannot be expressed by rules .
• Any single Datalog Rules can be expressed in relational algebra , but Datalog Recursion can be expressed , Relational algebra cannot .
  • because IDB Predicates can also appear in the body , Then the tuple of the rule header can be fed back to the rule body , So as to generate more tuples for the header .