当前位置:网站首页>"Statistical learning methods (2nd Edition)" Li Hang Chapter 14 clustering method mind map notes and after-school exercise answers (detailed steps) K-means hierarchical clustering Chapter 14
"Statistical learning methods (2nd Edition)" Li Hang Chapter 14 clustering method mind map notes and after-school exercise answers (detailed steps) K-means hierarchical clustering Chapter 14
2022-07-24 05:50:00 【Ml -- xiaoxiaobai】
Mind mapping :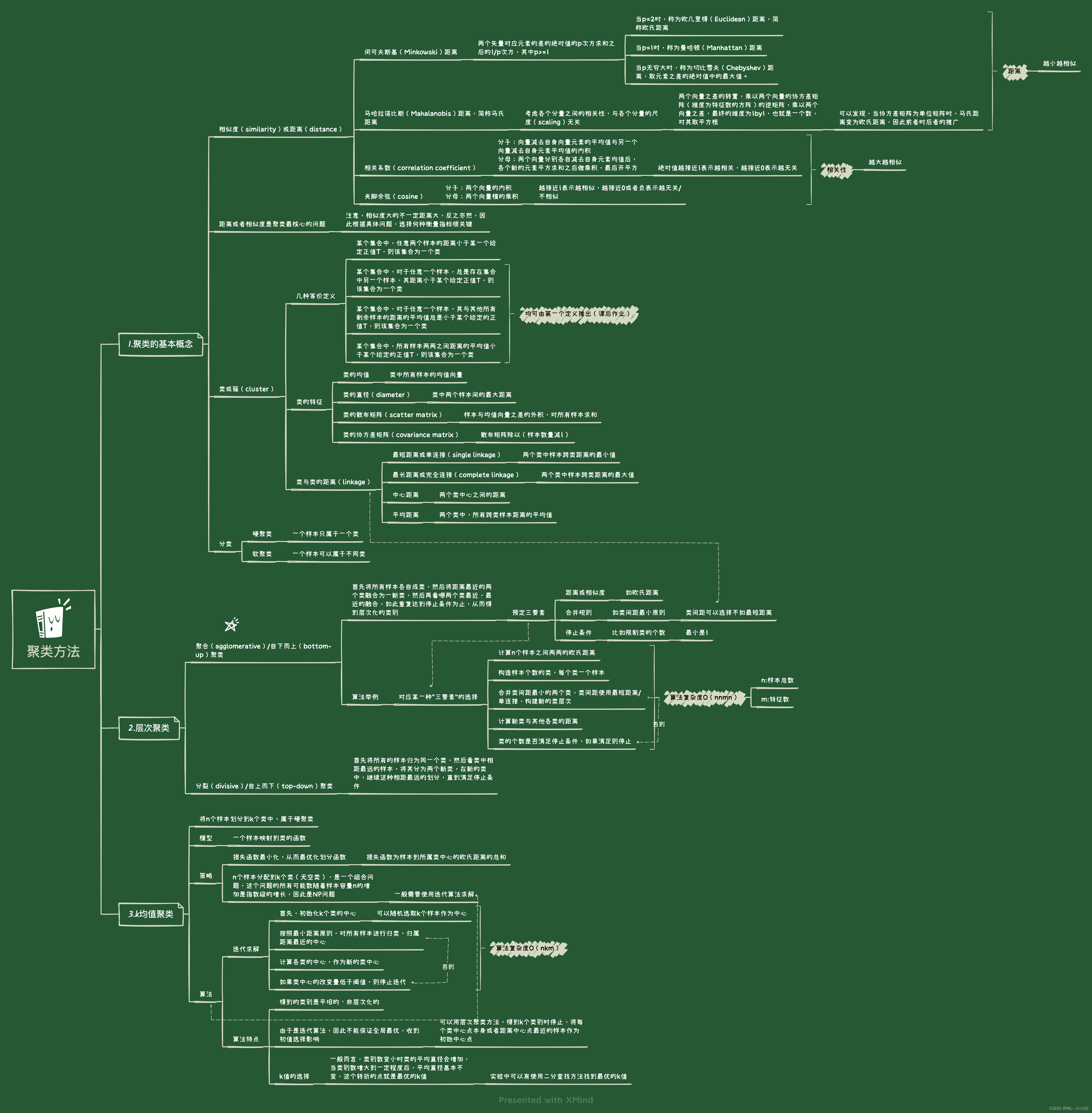
14.1
Try to write a split Clustering Algorithm , Clustering data from top to bottom , And the algorithm complexity is given .
i. Calculation n The distance between two samples , And treat all samples as a class , Take the maximum distance between samples as the class diameter ;
ii. For the class with the largest diameter , The farthest distance between them , That is, two samples with a distance of class diameter are divided into two new classes , Other samples of this kind are nearby ( Relative to the two selected samples ) Fall into one of two categories ;
iii. If the number of categories reaches the stop condition ( Preset classification book ) Then stop , Or go back to ii. step .
Model complexity O(nnmn), And polymerization (agglomerative) The algorithm complexity is the same .
14.2
Among the four definitions of proof class or cluster , The first definition can lead to the other three definitions .
The first definition introduces the second definition :
Reduction to absurdity :
If there is no such x i x_{i} xi, That means , Take any one x i x_{i} xi There are d i j > T d_{ij} > T dij>T , This contradicts the definition , Therefore, the original proposition holds .
The first definition introduces the third definition :
prove :
From the first definition we know : d i j ≤ T d_{ij} \leq T dij≤T, Then there are :
1 n G − 1 ∑ x j ∈ G d i j ≤ 1 n G − 1 ∑ x j ∈ G T = n G − 1 n G − 1 T = T \frac{1}{n_{G}-1} \sum_{x_{j} \in G} d_{i j} \leq \frac{1}{n_{G}-1} \sum_{x_{j} \in G} T = \frac{n_{G}-1}{n_{G}-1} T = T nG−11xj∈G∑dij≤nG−11xj∈G∑T=nG−1nG−1T=T
The first definition introduces the fourth definition :
prove :
1 n G n G − 1 ∑ x i ∈ G ∑ x j ∈ G d i j = 1 n G n G − 1 ∑ x i ∈ G ∑ x j ∈ G a n d x j ≠ x i d i j ≤ 1 n G n G − 1 ∑ x i ∈ G ∑ x j ∈ G a n d x j ≠ x i T ≤ T 1 n G n G − 1 ∑ x i ∈ G ∑ x j ∈ G a n d x j ≠ x i 1 ≤ T \frac{1}{n_{G} n_{G}-1} \sum_{x_{i} \in G} \sum_{x_{j} \in G} d_{i j} = \frac{1}{n_{G} n_{G}-1} \sum_{x_{i} \in G} \sum_{x_{j} \in G \; and \; x_{j} \neq x_{i}} d_{i j} \leq \frac{1}{n_{G} n_{G}-1} \sum_{x_{i} \in G} \sum_{x_{j} \in G \; and \; x_{j} \neq x_{i}} T \leq T \frac{1}{n_{G} n_{G}-1} \sum_{x_{i} \in G} \sum_{x_{j} \in G \; and \; x_{j} \neq x_{i}} 1 \leq T nGnG−11xi∈G∑xj∈G∑dij=nGnG−11xi∈G∑xj∈Gandxj=xi∑dij≤nGnG−11xi∈G∑xj∈Gandxj=xi∑T≤TnGnG−11xi∈G∑xj∈Gandxj=xi∑1≤T
The first equal sign is because the distance from the sample itself to itself is 0, namely d i i = 0 d_{ii}=0 dii=0, in addition $d_{ij} \leq V $ It is completely equivalent to definition one .
14.3
Proof formula (14.21) establish , namely k The possible solution of the mean is ( About the number of samples ) Exponential .
This is a combinatorial problem , It's time to recall the content of high school mathematics ( High school permutation ), In essence n Put a ball in k Boxes (k<n), How many kinds of playing methods are there , And pay attention , The box cannot be empty .
First , For the case of not considering whether the box is empty , Altogether k n k^{n} kn Maybe , We should focus on removing the empty box , It is difficult for us to write expressions directly, for example, there are several cases when there is only one box empty , But it's easy to write the possible number of at least one box empty :
( k 1 ) ( k − 1 ) n \left(\begin{array}{l}k \\ 1\end{array}\right)(k-1)^{n} (k1)(k−1)n
however , For 1 The case of an empty box does include , But for 2 There are repeated calculations in the case of empty boxes or more , Such as the 5 Boxes , We counted, for example 2 An empty box , But if the second 3 One is also empty , Then count when the second one is empty , The third one is also counted when it is empty . therefore , All greater than or equal to 2 The cases of empty boxes have been calculated repeatedly , To remove the weight, we must continue to calculate “ There are at least 2 An empty box ” The possible number of :
( k 2 ) ( k − 2 ) n \left(\begin{array}{l}k \\ 2\end{array}\right)(k-2)^{n} (k2)(k−2)n
similarly , Then found , This part happens to be 2 The possible number of empty boxes is no problem , But greater than or equal to 3 The case of empty boxes is calculated repeatedly , Therefore, it is still necessary to remove the weight and calculate :
( k 3 ) ( k − 3 ) n , ( k 4 ) ( k − 4 ) n , ( k 5 ) ( k − 5 ) n ⋯ ( k k ) ( k − k ) n \left(\begin{array}{l}k \\ 3\end{array}\right)(k-3)^{n}, \left(\begin{array}{l}k \\ 4\end{array}\right)(k-4)^{n}, \left(\begin{array}{l}k \\ 5\end{array}\right)(k-5)^{n} \cdots \left(\begin{array}{l}k \\ k\end{array}\right)(k-k)^{n} (k3)(k−3)n,(k4)(k−4)n,(k5)(k−5)n⋯(kk)(k−k)n
then , We can always use subtract At least one empty box , Compensate for double counting , need add At least two empty boxes , Also in order to compensate for the double counting problem , need subtract At least three empty boxes , therefore , There is one Minus sign Of alternate , The final possible number is :
k n = ( k 1 ) ( k − 1 ) n + ( k 2 ) ( k − 2 ) n − ⋯ + ( − 1 ) k ( k k ) ( k − k ) n = ∑ l = 0 k ( − 1 ) l ( k l ) ( k − l ) n k^{n}=\left(\begin{array}{l}k \\ 1\end{array}\right)(k-1)^{n}+\left(\begin{array}{l}k \\ 2 \end{array}\right)(k-2)^{n}-\cdots+(-1)^{k}\left(\begin{array}{l}k \\ k \end{array}\right)(k-k)^{n}=\sum_{l=0}^{k}(-1)^{l}\left(\begin{array}{l}k \\ l \end{array}\right)(k-l)^{n} kn=(k1)(k−1)n+(k2)(k−2)n−⋯+(−1)k(kk)(k−k)n=l=0∑k(−1)l(kl)(k−l)n
then , The description above , Small balls are indistinguishable , But the box is different , Boxes such as the first empty and the fifth empty are different , We want to eliminate this difference, so we have to divide by k ! k! k!
thus :
S ( n , k ) = 1 k ! ∑ l = 0 k ( − 1 ) l ( k l ) ( k − l ) n = 1 k ! ∑ l = 0 k − 1 ( − 1 ) l ( k l ) ( k − l ) n = = = = = z = k-l 1 k ! ∑ z = k 1 ( − 1 ) k − z ( k k − z ) z n = = = = = z = l 1 k ! ∑ l = 1 k ( − 1 ) k − l ( k k − l ) l n = 1 k ! ∑ l = 1 k ( − 1 ) k − l ( k l ) l n \begin{aligned} S(n, k) & =\frac{1}{k !} \sum_{l=0}^{k}(-1)^{l}\left(\begin{array}{l}k \\ l \end{array}\right)(k-l)^{n} \\ & =\frac{1}{k !} \sum_{l=0}^{k-1}(-1)^{l}\left(\begin{array}{l}k \\ l \end{array}\right)(k-l)^{n} \\ & \overset{\text{z = k-l}}{=====} \frac{1}{k !} \sum_{z=k}^{1}(-1)^{k-z}\left(\begin{array}{l}k \\ k-z \end{array}\right) z^{n} \\ & \overset{\text{z = l}}{=====} \frac{1}{k !} \sum_{l=1}^{k}(-1)^{k-l}\left(\begin{array}{l}k \\ k-l \end{array}\right) l^{n} \\ & =\frac{1}{k !} \sum_{l=1}^{k}(-1)^{k-l}\left(\begin{array}{l}k \\ l \end{array}\right) l^{n} \end{aligned} S(n,k)=k!1l=0∑k(−1)l(kl)(k−l)n=k!1l=0∑k−1(−1)l(kl)(k−l)n=====z = k-lk!1z=k∑1(−1)k−z(kk−z)zn=====z = lk!1l=1∑k(−1)k−l(kk−l)ln=k!1l=1∑k(−1)k−l(kl)ln
the last equal uses the fact that: ( k k − l ) = ( k l ) \\ \text{the last equal uses the fact that:} \left(\begin{array}{l}k \\ k - l \end{array}\right) = \left(\begin{array}{l}k \\ l \end{array}\right) the last equal uses the fact that:(kk−l)=(kl)
14.4
Compare k Mean clustering and Gaussian mixture model plus EM Similarities and differences of algorithms .
identical :
Gaussian mixture model (GMM) Find the distribution of hidden variables and k Mean clustering (k-means) Can be used for clustering problems ;
GMM And for features k-means It can be used for dimension reduction ;
( The above two points show that both are good unsupervised learning methods )
GMM And k-means In terms of strategy “ Loss / distance ” Minimal optimization strategy ;
GMM And k-means In the actual algorithm, the idea of iterative solution is used , The former uses EM Algorithm , The latter uses the iteration of distance , Both iterative algorithms have two steps , Every step is to fix a variable , Optimize another , These two ideas are the same , The former ,E Step fixed is Q Form of function , Calculation E,Q Step fixed is E The distribution of , to update Q, For the latter , First fix the classification function , Update the center point , Then fix the central store , Update classification ;
Both algorithms determine that it is not the global optimal solution , Is the local optimal solution , Therefore, the final result is related to the selection of initial value .
Different :
GMM Equivalent to soft clustering , Samples have certain probability from different Gaussian distributions , The final result of its learning is conditional probability distribution , It converges faster , Can handle larger data sets ;
k-means It belongs to hard clustering , Slow convergence .
边栏推荐
- [vSphere high availability] working principle of host and virtual machine fault monitoring
- Delete the weight of the head part of the classification network pre training weight and modify the weight name
- 数据归一化
- Zotero Quick Start Guide
- The method of using bat command to quickly create system restore point
- Similarities and differences of ODS, data mart and data warehouse
- 第四章 决策树总结
- Inventory of well-known source code mall systems at home and abroad
- Flink task, sub task, task slot and parallelism
- Read "Enlightenment: a 20-year career experience of an IT executive"
猜你喜欢
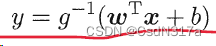
第三章 线性模型总结

Canal+kafka actual combat (monitor MySQL binlog to realize data synchronization)

plsql查询数据乱码

《信号与系统》(吴京)部分课后习题答案与解析

多商户商城系统功能拆解04讲-平台端商家入驻

学习率余弦退火衰减之后的loss

Multi merchant mall system function disassembly lecture 05 - main business categories of platform merchants

Mysqldump export Chinese garbled code

Introduction to PC mall module of e-commerce system

【mycat】mycat介绍
随机推荐
多商户商城系统功能拆解10讲-平台端商品单位
如何快速打通CRM系统和ERP系统,实现业务流程自动化流转
Erp+rpa opens up the enterprise information island, and the enterprise benefits are doubled
Likeshop single merchant SaaS mall system opens unlimited
Flink task, sub task, task slot and parallelism
《机器学习》(周志华) 第4章 决策树 学习心得 笔记
likeshop单商户SAAS商城系统无限多开
【mycat】mycat相关概念
[activiti] activiti introduction
多商户商城系统功能拆解14讲-平台端会员等级
Inventory of well-known source code mall systems at home and abroad
统计信号处理小作业——瑞利分布噪声中确定性直流信号的检测
Positional argument after keyword argument
Multi merchant mall system function disassembly Lecture 14 - platform side member level
SqlServer 完全删除
【activiti】activiti系统表说明
【activiti】activiti流程引擎配置类
多商户商城系统功能拆解05讲-平台端商家主营类目
Multi merchant mall system function disassembly lecture 07 - platform side commodity management
What do programmers often mean by API? What are the API types?