Combat readiness mathematical modeling 32 correlation analysis 2

Catalog

One 、 Pearson correlation coefficient

Two 、 Spearman correlation coefficient

3、 ... and 、 Canonical correlation analysis

1- Definition and specific steps

 2- Typical cases of correlation analysis 1

3- Typical cases of correlation analysis 2

---

This section focuses on two types of correlation analysis ,pearson and spearman, They can measure the correlation between two variables , We need to meet different conditions according to the data , Select different correlation coefficients for calculation and analysis , Introduce some details , Personal feelings are more important , Prevent the abuse of correlation analysis . meanwhile , We also discuss the application of canonical correlation analysis , A multivariate linear statistical method mainly used to solve the correlation between two groups of variables .

One 、 Pearson correlation coefficient

Let's take a look at the use requirements of Pearson and Spearman , For Pearson, the variables are required to be continuous data , And the variables have a linear relationship , And the data should obey the normal distribution , And generally, Pearson requires to use the correlation test between fixed distance and fixed distance variables , Sequencing and sequencing variables require Spearman .

Because there are many limitations of Pearson correlation test , We need to verify the restrictions before using , Whether it is a constant distance variable and whether it is continuous can be directly seen , So we first need to test the linearity of the variables , adopt SPSS Draw a matrix scatter , To determine whether there is a linear relationship between variables , There must be a linear relationship , To use the Pearson test .

Let's just look at an example , As follows ：

First step ： For data , We'd better start with descriptive statistics , This is a good habit , Is to calculate the maximum value of each index , mean value , Standard deviation , Skewness and kurtosis , It can be used SPSS perhaps MATLAB Such as implementation , Of course EXCEL It's fine too , Ha ha ha ha .

SPSS The method of describing statistics is simple , After importing data , Select descriptive statistics , Import variables into , It can be calculated automatically , As shown below .

Of course MATLAB Programming is also very simple , The code is as follows ：

clear; clc
load('test_data.mat')
format short g
% Descriptive statistics 
Min = min(test) ;
Max = max(test) ;
Mean = mean(test) ;
Median = median(test) ;
Skewness = skewness(test) ; % skewness 
Kurtosis = kurtosis(test) ; % kurtosis 
Std = std(test) ;
Result = [Min; Max; Mean; Median; Skewness; Kurtosis; Std] ;
disp(' The descriptive statistics are as follows ：') ;
disp(Result) ;

The second step , Is the use of SPSS Plot the matrix scatter diagram , The specific operation is as follows , Select graphics -> Old dialog -> Scatter plot -> Matrix three scatter diagram , The matrix scatter diagram drawn is as follows , Of course , The above tabular data is randomly generated , Most normal models have linear relationships .

The third step , Assume that there is a linear relationship between the variables of the above scatter diagram , Now we will calculate the Pearson correlation coefficient , Specifically MATLAB The procedure is as follows , Of course with SPSS It can also be calculated .

% Calculate the Pearson correlation coefficient 
R = corrcoef(test) ;
disp(' The Pearson correlation coefficient is as follows ：') ;
%xlswrite('D:\r1.xlsx',R) ;
disp(R) ;

We can have a look SPSS The results of Pearson correlation analysis , As follows ：

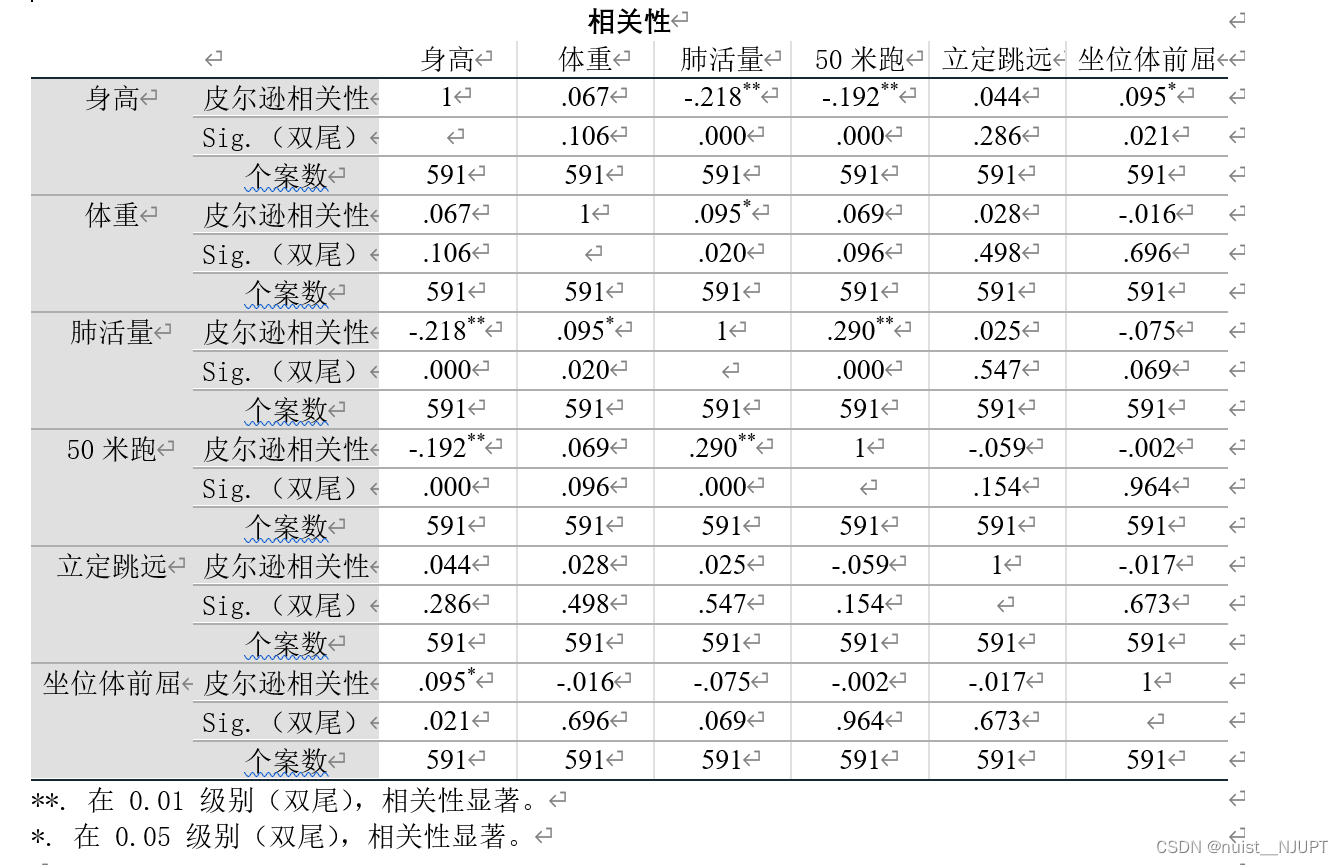
Test the hypothesis of the Pearson correlation coefficient ,p Value test ,p The smaller the value. , The closer the correlation is 1, adopt p It's worth rejecting the original assumption , It shows that Pearson correlation coefficient is significantly different from 0.

 

Step four , Normal distribution test is required , For large sample data , have access to JB Inspection and QQ Graph test . For small sample data , Use Shapiro - Wilke test .

JB Tested MATLAB The code is as follows , Be careful ： This original assumption is a normal distribution , We can't reject the original hypothesis to show that it obeys the normal distribution .

% For large sample data ,n>30 The data of , Normal distribution test , Use JB test , Jacques - Bella test 
[h,p] = jbtest(test(:,1),0.05) ; % Check whether the data in the first column is normally distributed 
% Check the data of all columns with a loop 
n_c = size(test, 2) ;
H = zeros(1,6) ;
P = zeros(1,6) ;
for i = 1 : n_c 
    [h,p] = jbtest(test(:,i), 0.05) ;
    H(i) = h ;
    P(i) = p ;
end
% If H be equal to 1 It means rejecting the original hypothesis ,P<0.5 You can reject the original hypothesis 
disp('H The values are as follows ：') ;
disp(H) ;
disp('P The values are as follows ：') ;
disp(P) ;

You can also use it QQ Fig. test whether the large sample obeys the normal distribution , But this only depends on the trend , Not accurate enough .

Draw... In this question QQ The code of the figure is as follows ：

subplot(2,3,1) ;
qqplot(test(:,1)) ;
title(' Height data and standard normal QQ chart ') ;
xlabel(' Standard normal number ') ;
ylabel(' Enter the number of samples ') ;
subplot(2,3,2);
qqplot(test(:,2)) ;
title(' Body weight data and standard normal QQ chart ') ;
xlabel(' Standard normal number ') ;
ylabel(' Enter the number of samples ') ;
subplot(2,3,3) ;
qqplot(test(:,3)) ;
title(' Vital capacity data and standard normal QQ chart ') ;
xlabel(' Standard normal number ') ;
ylabel(' Enter the number of samples ') ;
subplot(2,3,4);
qqplot(test(:,4)) ;
title('50 Meter run data and standard normal QQ chart ') ;
xlabel(' Standard normal number ') ;
ylabel(' Enter the number of samples ') ;
subplot(2,3,5) ;
qqplot(test(:,5)) ;
title(' Standing long jump data and standard normal QQ chart ') ;
xlabel(' Standard normal number ') ;
ylabel(' Enter the number of samples ') ;
subplot(2,3,6);
qqplot(test(:,6)) ;
title(' The forward flexion data of sitting posture are compared with that of standard normal QQ chart ') ;
xlabel(' Standard normal number ') ;
ylabel(' Enter the number of samples ') ;

QQ The graph is as follows , If it approximates to a straight line , It shows that the distribution is normal , As follows ：

  Use Shapiro for small sample data - Whether Wilke test obeys normal distribution ,SPSS Implementation steps , As follows ：

  The inspection results are as follows , If the significance is less than 0.05, Reject the null hypothesis , It means that the normal distribution is not obeyed .

  Pearson test , complete MATLAB The code is as follows ：

clear; clc
load('test_data.mat')
format short g
% Descriptive statistics 
Min = min(test) ;
Max = max(test) ;
Mean = mean(test) ;
Median = median(test) ;
Skewness = skewness(test) ; % skewness 
Kurtosis = kurtosis(test) ; % kurtosis 
Std = std(test) ;
Result = [Min; Max; Mean; Median; Skewness; Kurtosis; Std] ;
disp(' The descriptive statistics are as follows ：') ;
disp(Result) ;

% Before calculating the Pearson coefficient , You need to make a scatter plot , Observe whether the two groups of variables have a linear relationship according to the scatter diagram 
% We can use SPSS Achieve the above operation , Operate in the graphics options 


% For large sample data ,n>30 The data of , Normal distribution test , Use JB test , Jacques - Bella test 
[h,p] = jbtest(test(:,1),0.05) ; % Check whether the data in the first column is normally distributed 
% Check the data of all columns with a loop 
n_c = size(test, 2) ;
H = zeros(1,6) ;
P = zeros(1,6) ;
for i = 1 : n_c 
    [h,p] = jbtest(test(:,i), 0.05) ;
    H(i) = h ;
    P(i) = p ;
end
% If H be equal to 1 It means rejecting the original hypothesis ,P<0.5 You can reject the original hypothesis 
disp('H The values are as follows ：') ;
disp(H) ;
disp('P The values are as follows ：') ;
disp(P) ;

% For small sample data, Shapiro can be used ‐ Whether the Wilke test is a normal distribution 
% It can be used SPSS Realization 


% Of course, there is another way to test whether the distribution is normal Q-Q chart , Of course, this method requires a large amount of data , And just be able to see the trend 
subplot(2,3,1) ;
qqplot(test(:,1)) ;
title(' Height data and standard normal QQ chart ') ;
xlabel(' Standard normal number ') ;
ylabel(' Enter the number of samples ') ;
subplot(2,3,2);
qqplot(test(:,2)) ;
title(' Body weight data and standard normal QQ chart ') ;
xlabel(' Standard normal number ') ;
ylabel(' Enter the number of samples ') ;
subplot(2,3,3) ;
qqplot(test(:,3)) ;
title(' Vital capacity data and standard normal QQ chart ') ;
xlabel(' Standard normal number ') ;
ylabel(' Enter the number of samples ') ;
subplot(2,3,4);
qqplot(test(:,4)) ;
title('50 Meter run data and standard normal QQ chart ') ;
xlabel(' Standard normal number ') ;
ylabel(' Enter the number of samples ') ;
subplot(2,3,5) ;
qqplot(test(:,5)) ;
title(' Standing long jump data and standard normal QQ chart ') ;
xlabel(' Standard normal number ') ;
ylabel(' Enter the number of samples ') ;
subplot(2,3,6);
qqplot(test(:,6)) ;
title(' The forward flexion data of sitting posture are compared with that of standard normal QQ chart ') ;
xlabel(' Standard normal number ') ;
ylabel(' Enter the number of samples ') ;


% Calculate the Pearson correlation coefficient 
R = corrcoef(test) ;
disp(' The Pearson correlation coefficient is as follows ：') ;
%xlswrite('D:\r1.xlsx',R) ;
disp(R) ;

Two 、 Spearman correlation coefficient

Let's take another look at this comparison , When we find that it is not difficult to use Pearson correlation coefficient test , Then we can consider using    Spearman test , As follows ：

Use MATLAB and SPSS We can find the Spearman correlation coefficient , Given this time MATLAB Code ,SPSS Read another blog about correlation analysis .

clear; clc
load('test_data.mat')
format short g

% Calculate Spearman correlation coefficient 
R = corr(test, 'type', 'Spearman') ;
disp(' Spearman correlation coefficient is as follows ：') ;
disp(R) ;

  For Spearman's hypothesis test ,p Less than 0.05, You can reject the original hypothesis , Then explain and 0 There are significant differences , Otherwise, it is not difficult to reject the original assumption .

3、 ... and 、 Canonical correlation analysis

1- Definition and specific steps

General correlation analysis is used to analyze the correlation between two variables , If we need to consider the correlation between two sets of variables , Canonical correlation analysis .

We can first look at the idea of canonical correlation analysis , In fact, it is similar to dimensionality reduction , Is the linear combination of multiple variables , Form a comprehensive variable , Solving the correlation between comprehensive variables .

We use SPSS Perform canonical correlation analysis , Need to use SPSS24 Above version , As follows , First import the data ：

  Then the data is checked , Normal data are scaled , As shown below .

Then carry out canonical correlation analysis , Import two groups of variables respectively , as follows ：

 

  Next , The results of the analysis can be everywhere you want .

 2- Typical cases of correlation analysis 1

Carry out canonical correlation analysis on the following body index data , Refer to the above for specific steps . 

The results of my analysis are as follows ：

 

 

3- Typical cases of correlation analysis 2

We want to explore the relationship between the views of viewers and insiders on some TV programs ？
Audience rating comes from low education (led)、 Highly educated (hed) And the Internet (net) Investigate three , They form the first set of variables ;
The scores of the insiders come from artists including actors and directors (arti)、 issue (com) With the industry
Head of Department (man) Three , Form the second set of variables .

  Follow the above typical correlation analysis steps , My analysis results are as follows ：