[advanced binary tree] AVLTree - balanced binary search tree

Preface

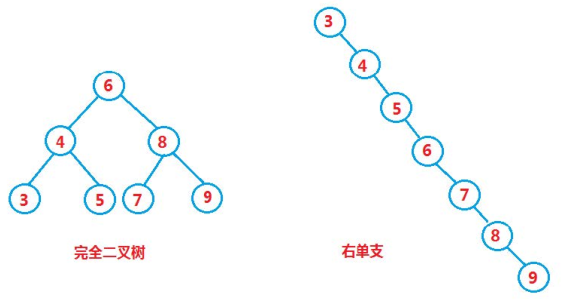
The insertion and deletion operations of binary search tree must first find , Search efficiency Represents the binary search tree Efficiency of each operation .

But binary search tree has its own defects , If The elements inserted into the tree are orderly or nearly orderly , The binary search tree will degenerate into a single branch tree , The time complexity is O(N), therefore map、set The underlying structure of equal correlation container is to balance the binary tree , The balanced binary search tree is used to realize .

In the best case , Yes n A binary search tree of nodes is a complete binary tree , The search efficiency is ：O(log₂N)

In the worst case , Yes n A binary search tree of nodes degenerates into a single branch tree , The search efficiency is ：O(N)

---

One 、AVL Trees

1.1 AVL The concept of tree

Balanced binary search trees （Self-balancing binary search tree）, also called AVL Trees

Although binary search tree can shorten the search efficiency , but The search tree will degenerate into a single ordered tree or a binary tree , Finding elements is equivalent to searching for elements in the sequence table , inefficiency . therefore , Two Russian mathematicians G.M.Adelson-Velskii and E.M.Landis stay 1962 In, he invented a method to solve the above problems ： When a new node is inserted into the binary search tree , If we can ensure that the absolute value of the height difference between the left and right subtrees of each node does not exceed 1( exceed 1 You need to adjust the nodes in the tree ), You can reduce the height of the tree , This reduces the average search length .

A tree AVL Trees , Or it's an empty tree , Or it is a binary search tree with the following properties ：

• The height difference between the left and right subtrees of each node （ It's called equilibrium factor Balance Factor） The absolute value of is not more than 1 (-1/0/1)

  Balance factor = The height of the right subtree - The height of the left subtree ： Used to judge whether balance operation is required

• Each subtree is a balanced binary search tree

If a binary search tree is highly balanced , It is AVL Trees .

Yes n Of nodes AVL Trees , The height can be maintained at log₂n, Its search time complexity O(log₂n).

reflection ： Why is the height difference between the left and right subtrees not specified as 0 Well ？

Because in 2、4 When the number of nodes is equal , It is impossible to achieve the same height on the left and right

---

1.2 AVL Definition of tree node

AVL The tree node is a trident chain structure , Except for the pointers to the left and right children , And a pointer to his father , Data fields are key value pairs , namely pair object , The equilibrium factor is also introduced , Used to judge whether balance operation is required .

// AVL Definition of tree node （KV Model ）
template<class K, class V>
struct AVLTreeNode
{
    
	pair<K, V> _kv;  //  Key value pair 
	int _bf;         //  Balance factor (balance factor) =  Height of right subtree  -  Height of left subtree 
	AVLTreeNode<K, V>* _left;
	AVLTreeNode<K, V>* _right;
	AVLTreeNode<K, V>* _parent; //  Parental pointer 

	//  Constructors 
	AVLTreeNode(const pair<K, V>& kv)
		:_kv(kv)
		,_bf(0)
		,_left(nullptr)
		,_right(nullptr)
		,_parent(nullptr)
	{
    }
};

// AVL The definition of a tree （KV Model ）
template<class K, class V>
class AVLTree
{
    
	typedef AVLTreeNode<K, V> Node;

private:
	Node* _root;

public:
	//  Member functions 
}

---

1.3 AVL Trees - Insert node

AVL The tree is based on the binary search tree and introduces the balance factor , therefore AVL The tree can also be regarded as a binary search tree . that AVL The process of inserting a tree can be divided into 3 Step ：

1. Insert new node
2. Update the balance factor of the tree
3. According to the balance factor of the updated tree , To control the balance of the tree （ Rotation operation ）

---

1.3.1 Insert new node

The insertion method is the same as that of binary search tree , To find the first , Insert again .

//  Insert node 
bool AVLTree::Insert(const pair<K, V>& kv)
{
    
    //  If the tree is empty , Insert the node directly 
    if (_root == nullptr)
    {
    
        _root = new Node(kv);
        return true;
    }

    //  If the tree is not empty , Find an empty location suitable for inserting nodes 
    Node* parent = nullptr;  //  Record the parent of the current node 
    Node* cur = _root;       //  Record current node 
    while (cur)
    {
    
        if(kv.first > cur->_kv.first) //  Insert node key values k Greater than the current node 
        {
    
            parent = cur;
            cur = cur->_right;
        }
        else if(kv.first < cur->_kv.first) //  Insert node key values k Less than the current node 
        {
     
            parent = cur;
            cur = cur->_left;
        }
        else //  Insert node key values k Equal to the current node 
        {
    
            return false;
        }
    }
    // while The loop ends , It indicates that an empty location suitable for inserting nodes has been found 

    //  Insert new node 
    cur = new Node(kv); //  Apply for a new node 
    //  Determine whether the current node is the father's left child or right child 
    if (cur->_kv.first > parent->_kv.first)
    {
    
        parent->_right = cur;
        cur->_parent = parent;

    }
    else
    {
    
        parent->_left = cur;
        cur->_parent = parent;
    }

    //...................................
    //  These write update balance factors , And control the balance of the tree 
    //...................................
    
    //  Insert the success 
    return true;
}

---

1.3.2 Update the balance factor of the tree

Insert 「 New node 」, From this node to all nodes on the branch through which the root passes （ Ancestor node ） The equilibrium factors of all are likely to be affected , According to different situations , Update their balance factor ：

• If inserted in 「 New node father 」 To the right of , Father's balance factor ++（ _bf++ ）
• If inserted in 「 New node father 」 Left side , Father's balance factor –（ _bf-- ）

「 New node father 」 After the balance factor is updated , It can be divided into 3 In this case ：

1、 If after the update , The equilibrium factor is 1 perhaps -1（ It must have been 0）, It means that the height of father's subtree has changed , Need to continue to update up .（ The worst ： Up to the root node ）

2、 If after the update , The equilibrium factor is 0（ It must have been 1 perhaps -1）, It means that the height of the father's subtree has not changed （ Because the short side was filled ）, There is no need to continue to update up .

3、 If after the update , Balance factor yes 2 perhaps -2, It shows that the subtree of the father is unbalanced , Need to rotate , Let it balance .

The code is as follows ：

while (parent) //  The worst ： Update to the root node 
{
    
    //  Update the balance factor of the new node's parent 

    if (cur == parent->_left) //  The new node is inserted to the left of the father 
    {
    
        parent->_bf--;
    }
    else //  The new node is inserted to the right of the parent 
    {
    
        parent->_bf++;
    }

    //  Check the balance factor of the new node's parent 

    // 1、 The height of father's subtree has changed , Need to continue to update up 
    if (parent->_bf == 1 || parent->_bf == -1)
    {
    
        cur = parent;
        parent = cur->_parent;
    }
    // 2、 The height of father's subtree has not changed , No need to continue updating 
    else if (parent->_bf == 0)
    {
    
        break;
    }
    // 3、 Father's subtree is unbalanced , Need to rotate 
    else if (parent->_bf == 2 || parent->_bf == -2)
    {
    
        //  Here we write to balance the tree , Code for rotation processing , It is divided into 4 In this case ：
        
        /*................................................*/
        // 3.1、 The left height of the parent node , Low on the right , It needs to be rotated to the right 
        if (parent->_bf == -2 && cur->_bf == -1)
        {
    
            //  Right single spin 
            treeRotateRight(parent); 
        }
        
        // 3.2、 The right height of the parent node , Low on the left , You need to turn left 
        else if (parent->_bf == 2 && cur->_bf == 1)
        {
    
            //  Left spin 
            treeRotateLeft(parent); 
        }
        
        // 3.3、 The left height of the parent node , And the parent node's left child's right height 
        else if(parent->_bf == -2 && cur->_bf == 1)
        {
    
            //  Double left and right 
            treeRotateLR(parent);
        }
        
        // 3.4、 The right height of the parent node , And the left height of the child on the right of the parent node 
        else if(parent->_bf == 2 && cur->_bf == -1)
        {
    
            //  Right left double rotation 
            treeRotateRL(parent);
        }
        
        else //  Only the above 4 In this case , Nothing else , So the error is directly reported here 
        {
    
            assert(false);
        }
        
        break; //  The rotation is complete , The tree is balanced , Exit loop 
        
        /*................................................*/
    }
    // 4、 In addition to the above 3 In this case , The equilibrium factor cannot have any other value , Error handling 
    else
    {
    
        assert(false);
    }
}

---

1.3.3 According to the updated BF The situation of , Perform balancing operation

If in a tree that was originally balanced AVL Insert a new node into the tree , May cause imbalance , At this point, the structure of the tree must be adjusted , Balance it . According to the insertion position of the node ,AVL The rotation of the tree is divided into 4 Kind of ：

The essence of rotation ： Following the rules of binary search tree , Balance left and right , Reduce the height of the whole tree .

What kind of rotation operation should be performed ？– The path that causes the rotation is a straight line or a single rotation , If it is a broken line, it is a double rotation .

Be careful ： The trees seen here , It could be a complete tree , It could also be a subtree .

---

① Right single spin - The new node is inserted into the leftmost part of the higher left subtree

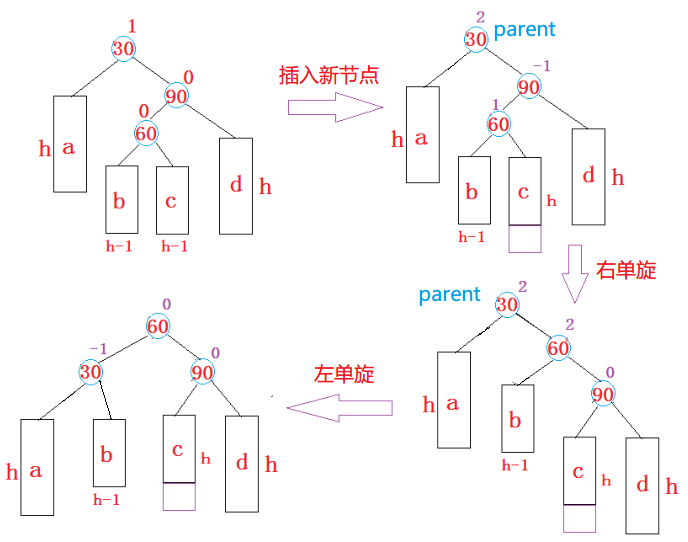
The new node is inserted into parent On the left tree of the left child , The resulting imbalance .

The above figure is before insertion ,AVL Trees are balanced , The new node is inserted into 30 The left subtree ( Be careful ： This is not the left child ) in ,30 The height of the left subtree is increased by one layer , Lead to 60 A binary tree with roots is unbalanced , Must let 60 Balance , Can only be 60 The height of the left subtree is reduced by one layer , Add a layer to the right subtree , About to lift the left sub tree up , such 60 Turn around , because 60 Than 30 Big , Can only make it 30 The right subtree , And if the 30 There are right subtrees , The value of the right subtree root must be greater than 30, Less than 60, Can only make it 60 The left subtree , When the rotation is complete , Update the balance factor of the node .

The condition that causes right monomorphism ：

• father Left high , Low on the right , So let father Turn right .
• parent The equilibrium factor of -2,parent The left child balance factor is -1, Observation found that , The equilibrium factors are all negative numbers , It means the left side is high , Also explained ==【 The path that causes the rotation is a straight line 】==, So we're going to do a right-handed operation .

Right single rotation operation ：

1. Give Way subL The right subtree subLR Become parent The left subtree （ because subLR The root node value of the right subtree of is greater than 30, Less than 60）
2. Give Way parent Become subL The right subtree （ because 60 Greater than 30）
3. Give Way subL Become the root of this subtree

• Before this step, you need to judge ：parent Root node , It is also an ordinary subtree
• If it's the root node , Update subL For a new root
• If it is an ordinary subtree （ It may be the left subtree of a node , It may also be a right subtree , You need to judge ）, And then update subL For the root node of this subtree

4. According to the structure of the tree , to update parent and subL The equilibrium factor of 0

In the course of rotation , Update the parent pointer , There are several situations to consider ：

1. subL The right subtree subLR Possible , May also be empty .（ Update only when it is not empty subL Right subtree subLR The parent pointer to ）
2. When the rotation is complete ,subL The parent node of , May be empty , It could be parent Original parent node .（ So update subL You need to judge before the parent pointer of ）

The code is as follows ：

in general , Is to adjust in turn subLR、parent、subL The position of the parent pointer .

//  Right single spin 
void treeRotateRight(Node* parent)
{
    
    // subL：parent The left child 
    // subLR：parent Left child's right child 
    Node* subL = parent->_left;
    Node* subLR = parent->_left->_right;

    // 1、 Give Way subL The right subtree subLR Become parent The left subtree 
    parent->_left = subLR;
    // 1.1、 If subLR Not empty 
    if (subLR)
    {
    
        subLR->_parent = parent; //  to update subLR Parents pointer , Point to parent
    }

    // 2、 Give Way parent Become subL The right subtree 
    subL->_right = parent;

    // 2.1、 Record parent Parent node 
    Node* ppNode = parent->_parent;

    // 2.2、 to update parent Parents pointer , Point to subL
    parent->_parent = subL;

    // 2.3、 Judge parent Is it the root node 
    //  Root node 
    if (parent == _root)
    {
    
        _root = subL;            //  to update subL For a new root 
        subL->_parent = nullptr; //  to update subL Parents pointer , Pointing empty 
    }
    //  Not the root node , Is an ordinary subtree 
    else
    {
    
        //  Judge parent Was it a left child or a right child 
        if (ppNode->_left == parent)
        {
    
            ppNode->_left = subL; // parent The original parent node takes over subL,subL For the root of this subtree 
        }
        else
        {
    
            ppNode->_right = subL;
        }

        subL->_parent = ppNode; //  to update subL Parents pointer 
    }

    //  Update according to the adjusted structure parent and subL The equilibrium factor of 
    parent->_bf = subL->_bf = 0;
}

---

② Left spin - The new node is inserted into the rightmost part of the higher right subtree

The new node is inserted into parent On the right tree of the right child , The resulting imbalance .

The condition that causes left single rotation ：

• father It's high on the right , Low on the left , So let father Turn left .
• parent The equilibrium factor of 2,parent The balance factor of the right child is 1, Observation found that , The equilibrium factors are all positive numbers , The description is high on the right , Also explained ==【 The path that causes the rotation is a straight line 】==, So we're going to use left-hand rotation .

Left single rotation operation ：

1. Give Way subR The left subtree subRL Become parent The right subtree （ because subRL The root node value of the left subtree of is greater than 30, Less than 60）
2. Give Way parent Become subR The left subtree （ because 30 Less than 60）
3. Give Way subR Become the root of this subtree
   • Before this step, you need to judge ：parent Root node , It is also an ordinary subtree
   • If it's the root node , Update subR For a new root
   • If it is an ordinary subtree （ It may be the left subtree of a node , It may also be a right subtree , You need to judge ）, And then update subR For the root node of this subtree
4. According to the structure of the tree , to update parent and subR The equilibrium factor of 0

In the course of rotation , Update the parent pointer , There are several situations to consider ：

1. subR The left subtree subRL Possible , May also be empty .（ Update only when it is not empty subR The left subtree subRL The parent pointer to ）
2. When the rotation is complete ,subR The parent node of , May be empty , It could be parent Original parent node .（ So update subR You need to judge before the parent pointer of ）

The code is as follows ：

in general , Is to adjust in turn subRL、parent、subR The position of the parent pointer .

//  Left spin 
void treeRotateLeft(Node* parent)
{
    
    // subR： Father's right child 
    // subRL： Father's right child's left child （ Bigger than father , Less than subR）
    Node* subR = parent->_right;
    Node* subRL = subR->_left;

    // 1、 Give Way subRL Become a father's right subtree 
    parent->_right = subRL;
    //  If subRL Not empty 
    if (subRL)
    {
    
        subRL->_parent = parent; //  to update subRL Parental pointer , Point to parent
    }

    // 2、 Give Way parent Become subR The left subtree 
    subR->_left = parent;

    // 2.1、 Record first parent The parent node of 
    Node* ppNode = parent->_parent;

    // 2.2、 to update parent The point of the parental pointer 
    parent->_parent = subR;

    // 2.3、 Judge parent Is it the root node 
    //  Root node 
    if (parent == _root)
    {
    
        _root = subR;            // subR For a new root 
        subR->_parent = nullptr; // subR The parent pointer points to null 
    }
    //  Not the root node , Is an ordinary subtree 
    else
    {
    
        //  Judge parent Was it a left child or a right child 
        if (ppNode->_left == parent)
        {
    
            ppNode->_left = subR; // parent The original parent node takes over subR,subR For the root of this subtree 
        }
        else
        {
    
            ppNode->_right = subR;
        }

        subR->_parent = ppNode; //  to update subR Parents pointer 
    }

    //  According to the structure of the tree , to update parent and subR The equilibrium factor of 
    parent->_bf = subR->_bf = 0;
}

---

③ Double left and right - The new node is inserted to the right of the higher left subtree

The new node is inserted into parent On the right tree of the left child , The resulting imbalance .

At this time, we need to be right first parent The right child makes a left rotation , Right again parent Make a right-handed rotation .

A phenomenon can be observed here ：

node 60 The left and right subtrees of are separated , The left subtree finally becomes 30 The right subtree , The right subtree finally becomes 90 The left subtree .

The picture below is h = 0 The situation of ：

The conditions for the initiation of double rotation ：

• The path that causes the rotation is a straight line or a single rotation , If it is a broken line, it is a double rotation
• parent The equilibrium factor of -2,parent The left child balance factor is 1, Observation found that , The balance factor is one negative and one positive , explain 「 The left child is tall on the right 」,「 Father is tall on his left 」, Also explained ==【 The path causing the rotation is a polyline 】==, So we have to first 「 Perform left-hand rotation on the left child 」, Again 「 Perform right-hand rotation on the father 」.

After left-right double rotation operation , According to the structure of the tree , When updating the balance factor , We need to pay attention to ：

Insert the new node at a different location , After left and right double spin , The structure of the tree will be different , The balance factor will also vary , There are three situations ：

1. The new node is inserted into 「parent Left child's right subtree 」 Of Left edge
2. The new node is inserted into 「parent Left child's right subtree 」 Of Right edge
3. The new node is 「parent Left child's right child 」

A phenomenon can be observed here , According to this phenomenon, we can deduce the equilibrium factor after rotation ：

node 60 The left and right subtrees of are separated , The left subtree eventually becomes a node 30 The right subtree , The right subtree eventually becomes a node 90 The left subtree .

The code is as follows ：

//  Double left and right 
void treeRotateLR(Node* parent)
{
    
    Node* subL = parent->_left; //  Record parent The left child 
    Node* subLR = subL->_right; //  Record parent The left child, the right child 

    //  Before spinning , Because the new node is inserted in a different location ,subLR The equilibrium factor may be -1/0/1

    int bf = subLR->_bf; //  Record subLR The equilibrium factor of 

    treeRotateLeft(parent->_left); //  First pair parent The left child of carries out left single rotation 
    treeRotateRight(parent);       //  Right again parent Make a right spin 

    //  After the rotation is complete , Adjust the balance factor of other nodes according to the situation 
    if (bf == -1)
    {
    
        parent->_bf = 1;
        subL->_bf = 0;
        subLR->_bf = 0;
    }
    else if (bf == 1)
    {
    
        parent->_bf = 0;
        subL->_bf = -1;
        subLR->_bf = 0;
    }
    else if (bf == 0)
    {
    
        parent->_bf = 0;
        subL->_bf = 0;
        subLR->_bf = 0;
    }
    else
    {
    
        assert(false);
    }
}

---

④ Right left double rotation - The new node is inserted to the left of the higher right subtree

The new node is inserted into parent On the left tree of the right child , The resulting imbalance .

At this time, we need to be right first parent The right child of carries out a right rotation , Right again parent Make a left turn .

​

This is a h = 1 The situation of ：

The conditions for the initiation of double rotation ：

• The path that causes the rotation is a straight line or a single rotation , If it is a broken line, it is a double rotation
• parent The equilibrium factor of 2, parent The balance factor of the right child is -1, Observation found that , The balance factor is one positive and one negative , explain 「 The right child is tall on the left 」,「 Father is tall on his right 」, Also explained ==【 The path causing the rotation is a polyline 】==, So we have to first 「 Rotate the right child 」, Again 「 Perform left-hand rotation on the father 」.

After left-right double rotation operation , According to the structure of the tree , When updating the balance factor , We need to pay attention to ：

Insert the new node at a different location , After right and left double spin , The structure of the tree will be different , The balance factor will also vary , There are three situations ：

1. The new node is inserted into 「parent Right child's left tree 」 Of Left edge
2. The new node is inserted into 「parent Right child's left tree 」 Of Right edge
3. The new node is 「parent Right child's left child 」

A phenomenon can be observed here , According to this phenomenon, we can deduce the equilibrium factor after rotation ：

node 60 The left and right subtrees of are separated , The left subtree b Finally, it becomes a node 30 The right subtree , Right subtree c Finally, it becomes a node 90 The left subtree .

The code is as follows ：

//  Right left double rotation 
void treeRotateRL(Node* parent)
{
    
    Node* subR = parent->_right; //  Record parent The right child 
    Node* subRL = subR->_left;   //  Record parent My right child's left child 

    //  Before spinning , Because the new node is inserted in a different location ,subRL The equilibrium factor of may be -1/0/1

    int bf = subRL->_bf; //  Record subRL The equilibrium factor of 

    treeRotateRight(parent->_right); //  First pair parent The right child carries out right single rotation 
    treeRotateLeft(parent);          //  Right again parent Make the left radio selection 

    //  After the rotation is complete , Adjust the balance factors of other nodes according to the tree structure 
    if (bf == -1)
    {
    
        parent->_bf = 0;
        subR->_bf = 1;
        subRL->_bf = 0;
    }
    else if (bf == 1)
    {
    
        parent->_bf = -1;
        subR->_bf = 0;
        subRL->_bf = 0;
    }
    else if(bf == 0)
    {
    
        parent->_bf = 0;
        subR->_bf = 0;
        subRL->_bf = 0;
    }
    else
    {
    
        assert(false);
    }
}

---

1.4 AVL Verification of trees

AVL The tree is based on the binary search tree and adds the restriction of balance , So verify AVL Trees , There are two steps ：

1. Verify that it is a binary search tree

If the middle order traversal can get an ordered sequence , It is explained as a binary search tree .

2. Verify that it is a balanced tree

The absolute value of the height difference of each node subtree shall not exceed 1

Whether the balance factor of the node is calculated correctly

---

（1） First, write a function to calculate the current tree height

//  Calculate the height of the current tree 
int Height(Node* root)
{
    
    //  The current tree is empty , Then the height is 0
    if (root == nullptr)
        return 0;

    //  The current tree is not empty , Calculate the height of the left and right subtrees 
    int leftHeight = Height(root->_left);
    int rightHeight = Height(root->_right);

    //  The height of the current tree  =  The one with the highest height in the left and right subtrees 1
    return max(leftHeight, rightHeight) + 1;
}

（2） Check AVL Whether the tree is balanced , Train of thought ： A top-down solution to violence

//  Check AVL Whether the tree is balanced , Train of thought 
bool IsBalance1()
{
    
    return _IsBalance1(_root);
}
bool _IsBalance1(Node* root)
{
    
    //  The current tree is empty , The explanation is balanced 
    if (root == nullptr)
        return true;

    //  The current tree is not empty , Calculate the height of the left and right subtrees 
    int leftHeight = Height(root->_left);
    int rightHeight = Height(root->_right);

    if (rightHeight - leftHeight != root->_bf) //  Check whether the balance factor of the current tree is calculated correctly 
    {
    
        cout << " The balance factor is abnormal :" << root->_kv.first << endl;
    }
    
    //  The absolute value of subtracting the height of the left and right subtrees is less than 2, It shows that the current tree is balanced , Then continue to judge other subtrees 
    return abs(leftHeight - rightHeight) < 2
        && _IsBalance1(root->_left)
        && _IsBalance1(root->_right);
}

（3） Check AVL Whether the tree is balanced , Train of thought two ： An efficient bottom-up solution （ Dynamic programming , The solution of the previous subproblem , It can be used to solve the latter problem ）

//  Check AVL Whether the tree is balanced , Train of thought two 
bool IsBalance2()
{
    
    return _IsBalance2(_root) != -1;
}

int _IsBalance2(Node* root)
{
    
    //  First judge the left of the current tree 、 Whether the right subtree is balanced , Then judge whether the current tree is balanced 
    //  Unbalanced return -1, Balance returns the height of the current tree 

    //  The current tree is empty , Return to altitude 0
    if (root == nullptr)
        return 0;

    //  The current tree is not empty , Calculate the height of left and right subtrees respectively 
    int leftHeight = _IsBalance2(root->_left);
    int rightHeight = _IsBalance2(root->_right);
    
    if (rightHeight - leftHeight != root->_bf) //  Check whether the balance factor of the current tree is calculated correctly 
    {
    
        cout << " The balance factor is abnormal :" << root->_kv.first << endl;
    }
    
    //  The height of the left subtree is equal to -1、 The height of the right subtree is equal to -1、 The absolute value of the height difference between the left and right subtrees is greater than 1, Indicates that the current tree is unbalanced 
    if (leftHeight == -1 || rightHeight == -1 || abs(leftHeight - rightHeight) > 1)
        return -1;

    //  Run here , It shows that the current tree is balanced , Returns the height of the current tree 
    return max(leftHeight, rightHeight) + 1;
}

---

1.5 AVL Trees - Delete node （ understand ）

because AVL The tree is also a binary search tree , Nodes can be deleted in the form of binary search tree , Then update the balance factor , If there is an unbalanced tree , Rotate . Just different from binary search tree ,AVL Update the balance factor after deleting nodes in the tree , In the worst case, always adjust to the position of the root node .

---

1.6 AVL Tree performance

AVL The tree is an absolutely balanced binary search tree , Close to a complete binary tree , It requires that the absolute value of the height difference between the left and right subtrees of each node should not exceed 1, This can ensure efficient query time complexity , namely O(log₂N). But if you want to be right AVL The tree does some structure modification , Very poor performance , such as ： Maintain its absolute balance when inserting , The number of rotations is more , Worse, when deleting , It is possible to keep the rotation up to the root . therefore ： If you need a query efficient and orderly data structure , And the number of data is static ( That will not change ), You can consider AVL Trees , But a structure is often modified , It's not suitable for .

---