当前位置:网站首页>论文阅读 (54):DeepFool: A Simple and Accurate Method to Fool Deep Neural Networks
论文阅读 (54):DeepFool: A Simple and Accurate Method to Fool Deep Neural Networks
2022-06-23 16:49:00 【因吉】
文章目录
1 引入
1.1 题目
2016CVPR:简单愚弄深度神经网络 (DeepFool: A simple and accurate method to fool deep neural networks)
1.2 动机
深度神经网络在图像分类任务上的成就毋庸置疑。然而,这些架构已被证明对图像的小扰动缺乏健壮性,目前也缺乏有效的方法来准确计算深度分类器应对大规模数据集上扰动的鲁棒性。本文则对这些鲁棒性进行可靠量化。
1.3 代码
Torch:http://github.com/lts4/deepfool
1.4 Bib
@inproceedings{Moosavi:2016:25742582,
author = {Seyed-Mohsen Moosavi-Dezfooli and Alhussein Fawzi and Pascal Frossard},
title = {Deep{F}ool: A simple and accurate method to fool deep neural networks},
booktitle = {
{IEEE} Conference on Computer Vision and Pattern Recognition},
pages = {2574--2582},
year = {2016}
}
2 DeepFool
对于给定的分类器,定义一个最小对抗性扰动 r r r,其用于改变样本的评估标签 k ^ ( x ) \hat{k}(x) k^(x):
Δ ( x ; k ^ ) : = min r ∥ r ∥ 2 s . t . k ^ ( x + r ) ≠ k ^ ( x ) , (1) \tag{1} \Delta(x;\hat{k}):=\min_r\|r\|_2\qquad s.t. \qquad \hat{k}(x+r)\neq\hat{k}(x), Δ(x;k^):=rmin∥r∥2s.t.k^(x+r)=k^(x),(1)其中 x x x是输入图像。该式也称为 k ^ \hat{k} k^在点 x x x的健壮性,因此分类器 k ^ \hat{k} k^的健壮性定义为:
ρ adv ( k ^ ) = E x Δ ( x ; k ^ ) ∥ x ∥ 2 , (2) \tag{2} \rho_\text{adv}(\hat{k})=\mathbb{E}_x\frac{\Delta(x;\hat{k})}{\|x\|_2}, ρadv(k^)=Ex∥x∥2Δ(x;k^),(2)其中 E x \mathbb{E}_x Ex是数据集分布的期望。
3 DeepFool与二分类
二分类问题下,有 k ^ ( x ) = sign ( f ( x ) ) \hat{k}(x)=\text{sign}(f(x)) k^(x)=sign(f(x)),其中 f : R n → R f:\mathbb{R}^n\to \mathbf{R} f:Rn→R是一个图像分类函数。令 F = Δ { x : f ( x ) = 0 } \mathcal{F}\overset{\Delta}{=}\{x:f(x)=0\} F=Δ{ x:f(x)=0}表示 f f f在0处的level set。首先分析线性分类器 f ( x ) = w T x + b f(x)=w^Tx+b f(x)=wTx+b的情况,然后推导出可以应用于任何可微分二分类器的通用算法。
可以很容易看出线性 f f f在点 x 0 x_0 x0处的鲁棒性, Δ ( x ; f ) \Delta(x;f) Δ(x;f)等价于 x 0 x_0 x0到分隔超平面 F = { x : w T x + b = 0 } \mathcal{F}=\{x:w^Tx+b=0\} F={ x:wTx+b=0}的距离 (如图2),改变分类器决策的最小扰动对应于 x 0 x_0 x0到 F \mathcal{F} F的正交投影。一个用于描述该过程的封闭式公式如下:
r ∗ ( x 0 ) : = arg min ∥ r ∥ 2 s . t . sign ( f ( x 0 + r ) ) ≠ sign ( f ( x 0 ) ) = − f ( x 0 ) ∥ w ∥ 2 2 w . (3) \tag{3} r_*(x_0):=\argmin\|r\|_2\qquad s.t. \qquad\text{sign}(f(x_0+r))\neq\text{sign}(f(x_0))=-\frac{f(x_0)}{\|w\|_2^2}w. r∗(x0):=argmin∥r∥2s.t.sign(f(x0+r))=sign(f(x0))=−∥w∥22f(x0)w.(3)
假设 f f f一个一般性二分类可微分分类器,我们使用一个迭代策略来评估健壮性 Δ ( x 0 ; f ) \Delta(x_0;f) Δ(x0;f)。在每次迭代中, f f f围绕当前点 x i x_i xi线性化,线性分类器的最小化扰动计算为
arg min r i ∥ r i ∥ s . t . f ( x i ) + ∇ f ( x i ) T r i = 0. (4) \tag{4} \argmin_{r_i}\|r_i\|\qquad s.t.\qquad f(x_i)+\nabla f(x_i)^Tr_i=0. riargmin∥ri∥s.t.f(xi)+∇f(xi)Tri=0.(4)扰动 r i r_i ri在每次迭代中通过公式3计算,并在下一次迭代 x i + 1 x_{i+1} xi+1时更新。算法将在分类器的标志改变时停止。算法1总结了DeepFool针对二分类问题的过程。图3是一个可视化结果。

实际上,上述算法往往可以收敛到零水平集 F \mathcal{F} F上的一点。为了达到分类边界的另一边,最终的扰动 r ^ \hat{r} r^将乘以一个常量 1 + η 1+\eta 1+η,其中 η ≪ 1 \eta\ll1 η≪1。在实验中将设置为 0.02 0.02 0.02。
4 DeepFool与多分类
一对多是最常用的多分类策略,因此我们基于该策略来扩展DeepFool到多分类上。在该设置下,分类器将有 c c c个输出,因此分类器被定义为 f : R d → R c f:\mathbb{R}^d\to \mathbb{R}^c f:Rd→Rc且:
k ^ ( x ) = arg max k f k ( x ) , (5) \tag{5} \hat{k}(x)=\argmax_kf_k(x), k^(x)=kargmaxfk(x),(5)其中 f k ( x ) f_k(x) fk(x)是 f ( x ) f(x) f(x)在第 c c c类上的输出。与二分类相似,首先分析线性情况并推广到其他分类器。
4.1 线性多分类器
令 f ( x ) = W T x + b f(x)=W^Tx+b f(x)=WTx+b表示一个线性分类器,在一对多的策略下,愚弄分类器的最小扰动被重写为:
arg min r ∥ r ∥ 2 s . t . ∃ k : w k T ( x 0 + r ) + b k ≥ w k ^ ( x 0 ) T ( x 0 + r ) + b k ^ ( x 0 ) , (6) \tag{6} \argmin_r\|r\|_2\qquad s.t.\qquad\exists k:w_k^T(x_0+r)+b_k\geq w_{\hat{k}(x_0)}^T(x_0+r)+b_{\hat{k}(x_0)}, rargmin∥r∥2s.t.∃k:wkT(x0+r)+bk≥wk^(x0)T(x0+r)+bk^(x0),(6)其中 w k w_k wk是 W W W的第 k k k列。几何上,上述问题对应于计算 x 0 x_0 x0与凸多面体complement P P P之间的距离:
P = ⋂ k = 1 c { x : f k ^ ( x o ) ( x ) ≥ f k ( x ) } , (7) \tag{7} P=\bigcap_{k=1}^c\{x:f_{\hat{k}(x_o)}(x)\geq f_k(x)\}, P=k=1⋂c{ x:fk^(xo)(x)≥fk(x)},(7)其中 x 0 x_0 x0是位于 P P P内的点。我们定义这个距离为 d i s t ( x 0 , P c ) \mathbf{dist}(x_0,P^c) dist(x0,Pc)。多面体 P P P定义了 f f f输出标签 k ^ ( x 0 ) \hat{k}(x_0) k^(x0)的空间区域,如图4所示。
公式6的解决方案可以用封闭形式计算如下。令 l ^ ( x 0 ) \hat{l}(x_0) l^(x0)表示离 P P P的边界最近的一个超平面,例如图4中的 l ^ ( x 0 ) = 3 \hat{l}(x_0)=3 l^(x0)=3。形式上, l ^ ( x 0 ) \hat{l}(x_0) l^(x0)可以计算为:
l ^ ( x 0 ) = arg min k ≠ k ^ ( x 0 ) ∣ f k ( x 0 ) − f k ^ ( x 0 ) ( x 0 ) ∣ ∥ w k − w k ^ ( x 0 ) ∥ 2 . (8) \tag{8} \hat{l}\left({x}_{0}\right)=\underset{k \neq \hat{k}\left({x}_{0}\right)}{\arg \min } \frac{\left|f_{k}\left({x}_{0}\right)-f_{\hat{k}\left({x}_{0}\right)}\left({x}_{0}\right)\right|}{\left\|{w}_{k}-{w}_{\hat{k}\left({x}_{0}\right)}\right\|_{2}}. l^(x0)=k=k^(x0)argmin∥∥∥wk−wk^(x0)∥∥∥2∣∣∣fk(x0)−fk^(x0)(x0)∣∣∣.(8)最小扰动 r ∗ ( x 0 ) r_*(x_0) r∗(x0)是将 x 0 x_0 x0投影到由 l ^ ( x 0 ) \hat{l}(x_0) l^(x0)索引的超平面上的向量:
r ∗ ( x 0 ) = ∣ f l ^ ( x 0 ) ( x 0 ) − f k ^ ( x 0 ) ( x 0 ) ∣ ∥ w l ^ ( x 0 ) − w k ^ ( x 0 ) ∥ 2 2 ( w l ^ ( x 0 ) − w k ^ ( x 0 ) ) . (9) \tag{9} {r}_{*}\left({x}_{0}\right)=\frac{\left|f_{\hat{l}\left({x}_{0}\right)}\left({x}_{0}\right)-f_{\hat{k}\left({x}_{0}\right)}\left({x}_{0}\right)\right|}{\left\|{w}_{\hat{l}\left({x}_{0}\right)}-{w}_{\hat{k}\left({x}_{0}\right)}\right\|_{2}^{2}}\left({w}_{\hat{l}\left({x}_{0}\right)}-{w}_{\hat{k}\left({x}_{0}\right)}\right) . r∗(x0)=∥∥∥wl^(x0)−wk^(x0)∥∥∥22∣∣∣fl^(x0)(x0)−fk^(x0)(x0)∣∣∣(wl^(x0)−wk^(x0)).(9)换句话说,我们可以找到 x o x_o xo在 P P P的平面上的最近投影。
4.2 广义分类器
对于非线性分类器,公式7中描述分类器输出标签 k ^ ( x 0 ) \hat{k}(x_0) k^(x0)空间区域的集合 P P P不再是多面体。与二分类下的迭代求解类似,集合 P P P通过第 i i i轮迭代的多面体 P ~ i \tilde{P}_i P~i近似:
P ~ i = ⋂ k = 1 c { x : f k ( x i ) − f k ^ ( x 0 ) ( x i ) + ∇ f k ( x i ) T x − ∇ f k ^ ( x 0 ) ( x i ) T x ≤ 0 } . (10) \tag{10} \tilde{P}_i=\bigcap_{k=1}^c\left\{x:f_k(x_i)-f_{\hat{k}(x_0)}(x_i)+\nabla f_k(x_i)^Tx-\nabla f_{\hat{k}(x_0)}(x_i)^Tx\leq0\right\}. P~i=k=1⋂c{ x:fk(xi)−fk^(x0)(xi)+∇fk(xi)Tx−∇fk^(x0)(xi)Tx≤0}.(10)然后在每一次迭代中通过 d i s t ( x i , P ~ i ) \mathbf{dist}(x_i,\tilde{P}_i) dist(xi,P~i)来近似 d i s t ( x i , P i ) \mathbf{dist}(x_i,P_i) dist(xi,Pi)。算法2展示了该过程。应该注意的是,所提出的算法以贪婪的方式运行,不能保证收敛到公式1中的最优扰动。而实践中观察中的结果显示所提算法可以产生非常小的扰动,这被认为是最小扰动的良好近似。
4.3 ℓ p \ell_p ℓp范数的扩展版本
DeepFool的前述步骤均在 ℓ 2 \ell_2 ℓ2下进行,当在 ℓ p , p ∈ [ 1 , ∞ ) \ell_p,p\in[1,\infty) ℓp,p∈[1,∞)下约束时,算法2中的第10、11行需要被替换为:
l ^ ← arg min k ≠ k ^ ( x 0 ) ∣ f k ′ ∣ ∥ w k ′ ∥ q , (11) \tag{11} \hat{l} \leftarrow \underset{k \neq \hat{k}\left({x}_{0}\right)}{\arg \min } \frac{\left|f_{k}^{\prime}\right|}{\left\|{w}_{k}^{\prime}\right\|_{q}}, l^←k=k^(x0)argmin∥wk′∥q∣fk′∣,(11) r i ← ∣ f ı ^ ′ ∣ ∥ w ı ^ ′ ∥ q q ∣ w ı ^ ′ ∣ q − 1 ⊙ sign ( w l ^ ′ ) , (12) \tag{12} {r}_{i} \leftarrow \frac{\left|f_{\hat{\imath}}^{\prime}\right|}{\left\|{w}_{\hat{\imath}}^{\prime}\right\|_{q}^{q}}\left|{w}_{\hat{\imath}}^{\prime}\right|^{q-1} \odot \operatorname{sign}\left({w}_{\hat{l}}^{\prime}\right), ri←∥wı^′∥qq∣fı^′∣∣wı^′∣q−1⊙sign(wl^′),(12)
其中 ⊙ \odot ⊙是按元素相乘、 q = p p − 1 ⋅ q=\frac{p}{p-1} \cdot q=p−1p⋅。特别地当 p = ∞ p=\infty p=∞时,有:
l ^ ← arg min k ≠ k ^ ( x 0 ) ∣ f k ′ ∣ ∥ w k ′ ∥ 1 , (13) \tag{13} \hat{l} \leftarrow \underset{k \neq \hat{k}\left(\boldsymbol{x}_{0}\right)}{\arg \min } \frac{\left|f_{k}^{\prime}\right|}{\left\|\boldsymbol{w}_{k}^{\prime}\right\|_{1}}, l^←k=k^(x0)argmin∥wk′∥1∣fk′∣,(13) r i ← ∣ f l ^ ′ ∣ ∥ w l ^ ′ ∥ 1 sign ( w l ^ ′ ) . (14) \tag{14} \boldsymbol{r}_{i} \leftarrow \frac{\left|f_{\hat{l}}^{\prime}\right|}{\left\|\boldsymbol{w}_{\hat{l}}^{\prime}\right\|_{1}} \operatorname{sign}\left(\boldsymbol{w}_{\hat{l}}^{\prime}\right). ri←∥∥∥wl^′∥∥∥1∣∣∣fl^′∣∣∣sign(wl^′).(14)
边栏推荐
- Self supervised learning (SSL)
- Explanation of the principle and code implementation analysis of rainbow docking istio
- How code 39 check bits are calculated
- QT layout manager [qvboxlayout, qhboxlayout, qgridlayout]
- [qsetting and.Ini configuration files] and [create resources.qrc] in QT
- MySQL installation, configuration and uninstall
- Query the size of each table in the database
- FPN characteristic pyramid network
- Easyplayer mobile terminal plays webrtc protocol for a long time. Pressing the play page cannot close the "about us" page
- [JS reverse hundred examples] pedata encryption information and zlib Application of gunzipsync()
猜你喜欢

美团三面:聊聊你理解的Redis主从复制原理?

Performance test bottleneck tuning in 10 minutes! If you want to enter a large factory, you must know
![QT layout manager [qvboxlayout, qhboxlayout, qgridlayout]](/img/62/a0425a325f123ba91a7a69cf854d2c.png)
QT layout manager [qvboxlayout, qhboxlayout, qgridlayout]

FPN characteristic pyramid network
![[go] calling Alipay to scan code for payment in a sandbox environment](/img/d4/c6d72a697bc08f69f11121a15109b3.png)
[go] calling Alipay to scan code for payment in a sandbox environment

How important is 5g dual card dual access?

torch学习(一):环境配置
![[mae]masked autoencoders mask self encoder](/img/08/5ab2b0d5b81c723919046699bb6f6d.png)
[mae]masked autoencoders mask self encoder

Query the size of each table in the database
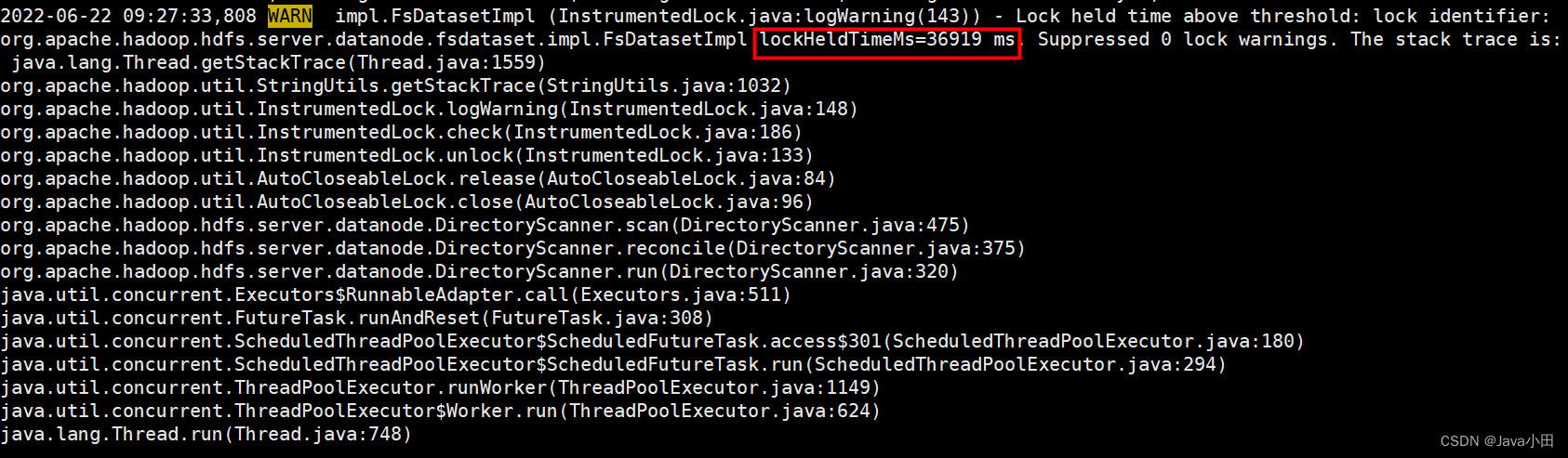
Troubleshooting of datanode entering stale status
随机推荐
B. Integers Shop-Hello 2022
Practice sharing of chaos engineering in stability management of cloud native Middleware
Goframe framework: graceful closing process
JS regular verification time test() method
Bypass rights
Ctfshow PHP features
QT布局管理器【QVBoxLayout,QHBoxLayout,QGridLayout】
How to quickly obtain and analyze the housing price in your city?
解析 | 模-数(A/D)转换器
6、VLAN
Baidu AI Cloud product upgrade Observatory in May
解答02:Smith圓為什麼能“上感下容 左串右並”?
Go unit test
Ner's past, present and future Overview - Future
How about stock online account opening and account opening process? Is online account opening safe?
ACM players take you to play with the array!
Goframe framework: basic auth Middleware
MySQL的 安装、配置、卸载
New function! Qianfan magic pen apaas December capability monthly report
January 5, 2022: there are four kinds of rhythms: AABB, ABAB and ABB