《统计学习方法（第2版）》李航 第14章 聚类方法 思维导图笔记 及 课后习题答案（步骤详细） k-均值 层次聚类 第十四章

思维导图：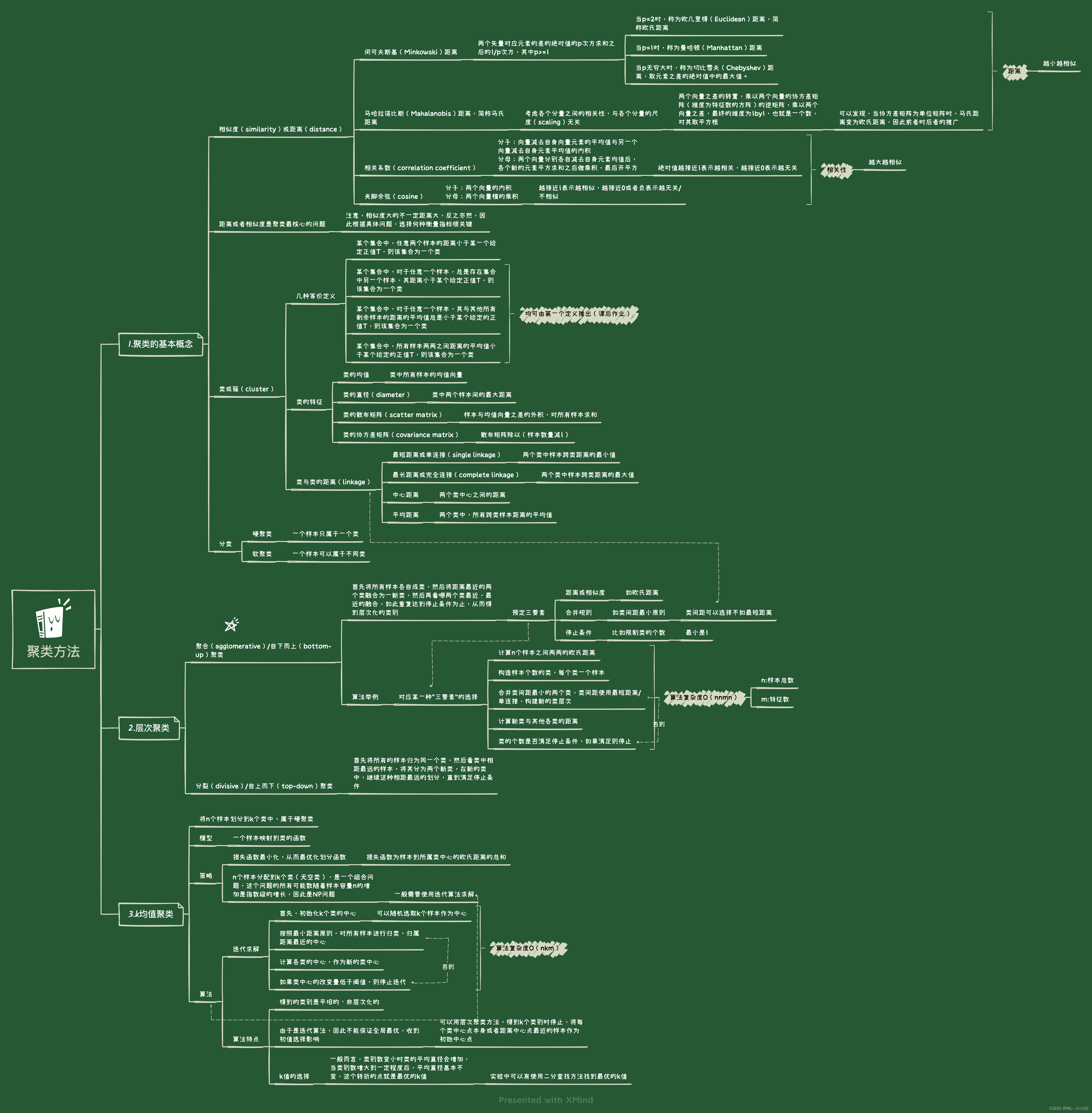

14.1

试写出分裂聚类算法，自上而下地对数据进行聚类，并给出其算法复杂度。

i. 计算n个样本两两之间的距离，并将所有样本看作一个类，将样本间最大距离作为类直径；

ii. 对于类直径最大的类，将其中相距最远，也就是距离为类直径的两个样本分成两个新类，该类其他样本就近（相对于那两个选中的样本）归于两个类之一；

iii. 如果类别个数达到停止条件（预设的分类书）则停止，否则回到ii.步骤。

模型复杂度O(nnmn),与聚合（agglomerative）算法复杂度相同。

14.2

证明类或簇的四个定义中，第一个定义可以推出其他三个定义。

第一个定义推出第二个定义：
反证法：
果不存在这样的$x_i$，那么意味着，任取一个$x_i$都有$d_{ij}>T$ ，这与定义一矛盾，因此原命题成立。

第一个定义推出第三个定义：
证明：
由第一个定义知：$d_{ij}\le T$，则有：
$$\frac{1}{n_G-1}\sum _{x_j\in G}{d}_{ij}\le \frac{1}{n_G-1}\sum _{x_j\in G}T=\frac{n_G-1}{n_G-1}T=T$$

第一个定义推出第四个定义：
证明：
$$\frac{1}{n_G{n}_G-1}\sum _{x_i\in G}\sum _{x_j\in G}{d}_{ij}=\frac{1}{n_G{n}_G-1}\sum _{x_i\in G}\sum _{x_j\in Gand{x}_j\ne x_i}{d}_{ij}\le \frac{1}{n_G{n}_G-1}\sum _{x_i\in G}\sum _{x_j\in Gand{x}_j\ne x_i}T\le T\frac{1}{n_G{n}_G-1}\sum _{x_i\in G}\sum _{x_j\in Gand{x}_j\ne x_i}1\le T$$
其中第一个等号是因为样本自身到自身的距离是0，即$d_{ii}=0$,另外$d_{ij} \leq V $与定义一完全等价。

14.3

证明式(14.21)成立，即k均值的可能的解是（关于样本数量）指数级的。

这个是一个组合问题，要好好回忆一下高中数学内容了（高中的排列组合），本质上就n个球放到k个盒子（k<n），一共有多少种放法，且注意，盒子不能有空着的。

首先，对于不考虑盒子空不空的情况，一共有$k^n$种可能，我们重点要将这里面空着盒子的情况去除，我们很难直接写出比如只有一个盒子空着有几种情况的表达式，但是容易写出至少有一个盒子空着的可能数：
$$\left(\begin{array}{l}k\\ 1\end{array}\right)(k-1{)}^n$$
但是，这里面对于1个空盒的情况确实包括了，但是对于2个及以上空盒的情况有重复的计算，比如有5个盒子，我们计数了比如第2个盒子空着的情况，但是后面假如第3个也是空的，那么在第二个空着的时候计数了，在第三个空着的时候同样计数了。因此，所有大于等于2个空盒的情况都被重复计算了，要去重就要继续计算“至少有2个空盒”的可能数：
$$\left(\begin{array}{l}k\\ 2\end{array}\right)(k-2{)}^n$$
同样地，这时发现，这部分里面恰好为2个空盒的可能数是没问题的，但是大于等于3个空盒的情况又重复计算了，因此仍然需要去重需要计算：
$$\left(\begin{array}{l}k\\ 3\end{array}\right)(k-3{)}^n，\left(\begin{array}{l}k\\ 4\end{array}\right)(k-4{)}^n，\left(\begin{array}{l}k\\ 5\end{array}\right)(k-5{)}^n\cdots \left(\begin{array}{l}k\\ k\end{array}\right)(k-k{)}^n$$
然后，我们用总可能减去至少一个空盒，补偿重复计算，需要加上至少二个空盒情况，同样为了补偿重复计入问题，需要减去至少三个空盒情况，因此，有个负号的交替，最终的可能数为：
$$k^n=\left(\begin{array}{l}k\\ 1\end{array}\right)(k-1{)}^n+\left(\begin{array}{l}k\\ 2\end{array}\right)(k-2{)}^n-\cdots +(-1{)}^k\left(\begin{array}{l}k\\ k\end{array}\right)(k-k{)}^n=\sum _{l=0}^k(-1{)}^l\left(\begin{array}{l}k\\ l\end{array}\right)(k-l{)}^n$$
然后，上面的描述，小球是无差别的，但是盒子是有差别的，盒子比如第一个空和第五个空是不同的情况，我们要消除这种不同因此要除以$k!$
从而:
$$\begin{array}{rl}S(n,k)& =\frac{1}{k!}\sum _{l=0}^k(-1{)}^l\left(\begin{array}{l}k\\ l\end{array}\right)(k-l{)}^n\\ & =\frac{1}{k!}\sum _{l=0}^{k-1}(-1{)}^l\left(\begin{array}{l}k\\ l\end{array}\right)(k-l{)}^n\\ & \stackrel{\text{z = k-l}}{=====}\frac{1}{k!}\sum _{z=k}^1(-1{)}^{k-z}\left(\begin{array}{l}k\\ k-z\end{array}\right)z^n\\ & \stackrel{\text{z = l}}{=====}\frac{1}{k!}\sum _{l=1}^k(-1{)}^{k-l}\left(\begin{array}{l}k\\ k-l\end{array}\right)l^n\\ & =\frac{1}{k!}\sum _{l=1}^k(-1{)}^{k-l}\left(\begin{array}{l}k\\ l\end{array}\right)l^n\end{array}$$
$$\text{the last equal uses the fact that:}\left(\begin{array}{l}k\\ k-l\end{array}\right)=\left(\begin{array}{l}k\\ l\end{array}\right)$$

14.4

比较k均值聚类与高斯混合模型加EM算法的异同。

相同：

高斯混合模型（GMM）寻找隐变量分布和k均值聚类（k-means）都可以用于聚类问题；
GMM和对于特征的k-means可以用于降维问题；
（以上两点说明二者都是很好的无监督学习方法）
GMM与k-means在策略上都是利用了“损失/距离”最小的优化策略；
GMM与k-means在实际的算法上都是利用了迭代求解的思想，前者使用EM算法，后者使用距离的迭代，两种迭代算法都有两步构成，每一步都是固定一个变量，优化另一个，这两种思想是相同的，前者，E步固定的是Q函数的形式，计算E，Q步固定的是E的分布，更新Q，对后者，先固定分类函数，更新中心点，再固定中心店，更新分类；
两者的算法都决定了不是全局最优解，是局部最优解，因此最终结果与初值选取有关。

不同:

GMM相当于软聚类，样本是有一定概率来自不同的高斯分布的，其学习的最终结果为条件概率分布，其收敛更快，可以处理更大的数据集；
k-means属于硬聚类，收敛较慢。