当前位置:网站首页>【GCN-RS】Are Graph Augmentations Necessary? Simple Graph Contrastive Learning for RS (SIGIR‘22)
【GCN-RS】Are Graph Augmentations Necessary? Simple Graph Contrastive Learning for RS (SIGIR‘22)
2022-07-25 11:11:00 【chad_lee】
Are Graph Augmentations Necessary? Simple Graph Contrastive Learning for Recommendation (SIGIR’22)

这篇文章抨击图对比学习不一定要扩展图结构,SGL那种方法复杂且收益微弱:

文章在SGL的基础上,测试不扩增图结构,直接对比学习:
L c l = ∑ i ∈ B − log exp ( z i ′ ⊤ z i ′ ′ / τ ) ∑ j ∈ B exp ( z i ′ ⊤ z j ′ ′ / τ ) \mathcal{L}_{c l}=\sum_{i \in \mathcal{B}}-\log \frac{\exp \left(\mathbf{z}_{i}^{\prime \top} \mathbf{z}_{i}^{\prime \prime} / \tau\right)}{\sum_{j \in \mathcal{B}} \exp \left(\mathbf{z}_{i}^{\prime \top} \mathbf{z}_{j}^{\prime \prime} / \tau\right)} Lcl=i∈B∑−log∑j∈Bexp(zi′⊤zj′′/τ)exp(zi′⊤zi′′/τ)
我曾经也做过实验,把这个公式的分子置为1,即不考虑扩增图结构后表征依然相似,NDCG指标反而升的更高,所以SGL的确实不太有用。
文章提出了一种非常简单的方法,直接在embedding上做扰动,不动图结构:

e i ′ = e i + Δ i ′ e i ′ ′ = e i + Δ i ′ ′ \begin{array}{r} e_{i}^{\prime}=e_{i}+\Delta_{i}^{\prime} \\ e_{i}^{\prime \prime}=e_{i}+\Delta_{i}^{\prime \prime} \end{array} ei′=ei+Δi′ei′′=ei+Δi′′
其中 Δ i ′ , Δ i ′ ′ \Delta_{i}^{\prime },\Delta_{i}^{\prime \prime} Δi′,Δi′′分别是随机扰动, Δ = Δ ˉ ⊙ sign ( e i ) , sign ( x ) , x < 0 \Delta=\bar{\Delta} \odot \operatorname{sign}\left(e_{i}\right), \operatorname{sign}(\mathrm{x}), x<0 Δ=Δˉ⊙sign(ei),sign(x),x<0则输出-1,否则1。 Δ ˉ ∼ U ( 0 , 1 ) \bar{\Delta} \sim U(0,1) Δˉ∼U(0,1)。因此这两个扰动可以看作在原始embedding的方向,各自伸缩了一些。然后带入对比学习loss,就可以用了。
在实现上就更简单暴力了,只是在每层embedding加扰动而已:
E ′ = 1 L ( ( A ~ ( 0 ) + Δ ( 1 ) ) + ( A ~ ( A ~ E ( 0 ) + Δ ( 1 ) ) + Δ ( 2 ) ) ) + … + ( A ~ L E ( 0 ) + A ~ L − 1 Δ ( 1 ) + … + A ~ Δ ( L − 1 ) + Δ ( L ) ) ) \begin{array}{r} \mathbf{E}^{\prime}=\frac{1}{L}\left(\left(\tilde{\mathbf{A}}^{(0)}+\Delta^{(1)}\right)+\left(\tilde{\mathbf{A}}\left(\tilde{\mathrm{A}} \mathrm{E}^{(0)}+\Delta^{(1)}\right)+\Delta^{(2)}\right)\right)+\ldots \\ \left.+\left(\tilde{\mathbf{A}}^{L} \mathbf{E}^{(0)}+\tilde{\mathbf{A}}^{L-1} \Delta^{(1)}+\ldots+\tilde{\mathbf{A}} \Delta^{(L-1)}+\Delta^{(L)}\right)\right) \end{array} E′=L1((A~(0)+Δ(1))+(A~(A~E(0)+Δ(1))+Δ(2)))+…+(A~LE(0)+A~L−1Δ(1)+…+A~Δ(L−1)+Δ(L)))
边栏推荐
- 11. Reading rumors spread with deep learning
- 'C:\xampp\php\ext\php_zip.dll' - %1 不是有效的 Win32 应用程序 解决
- 阿里云技术专家秦隆:可靠性保障必备——云上如何进行混沌工程
- PL/SQL入门,非常详细的笔记
- Classification parameter stack of JS common built-in object data types
- brpc源码解析(一)—— rpc服务添加以及服务器启动主要过程
- Hardware connection server TCP communication protocol gateway
- 【高并发】高并发场景下一种比读写锁更快的锁,看完我彻底折服了!!(建议收藏)
- 【多模态】《TransRec: Learning Transferable Recommendation from Mixture-of-Modality Feedback》 Arxiv‘22
- The JSP specification requires that an attribute name is preceded by whitespace
猜你喜欢
W5500 upload temperature and humidity to onenet platform

教你如何通过MCU配置S2E为TCP Server的工作模式

JS operator
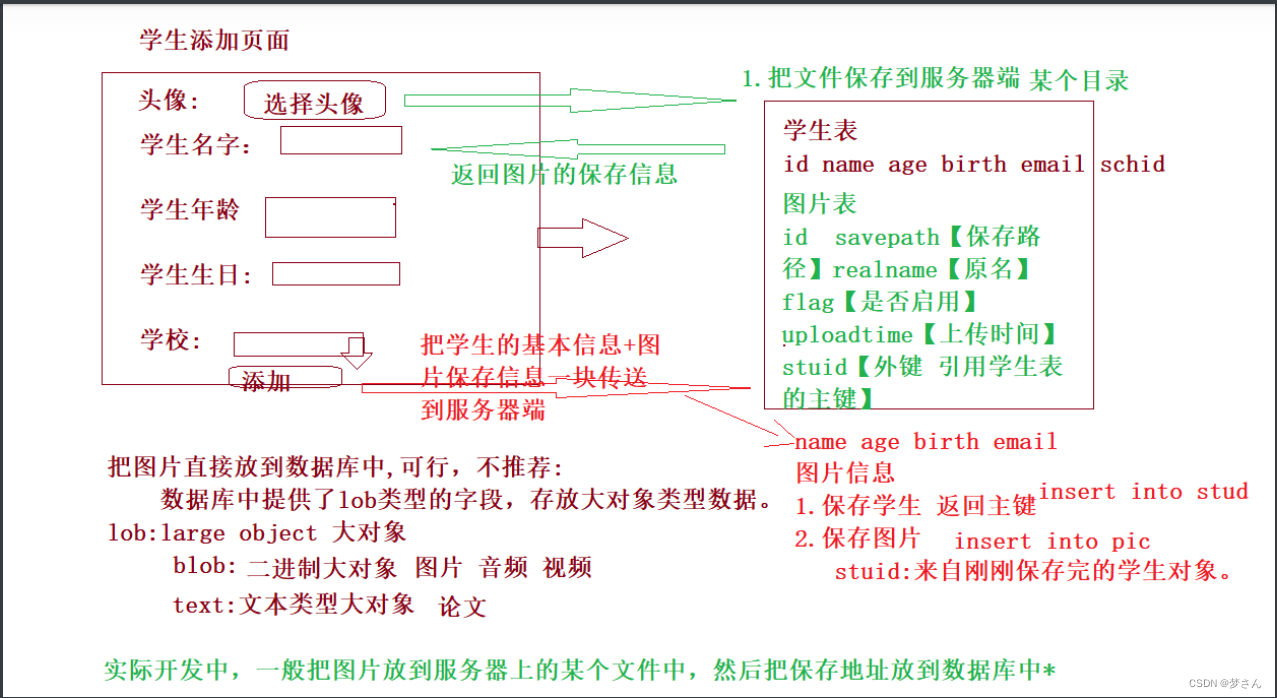
JDBC summary
winddows 计划任务执行bat 执行PHP文件 失败的解决办法

GPT plus money (OpenAI CLIP,DALL-E)

Differences in usage between tostring() and new string()
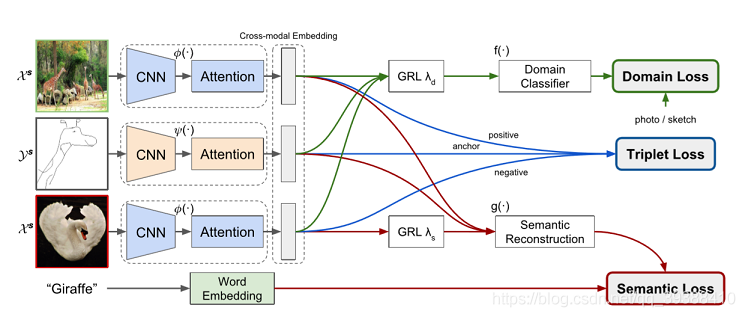
Zero-Shot Image Retrieval(零样本跨模态检索)
Video Caption(跨模态视频摘要/字幕生成)

Return and finally? Everyone, please look over here,
随机推荐
JS data types and mutual conversion
JS operator
GPT plus money (OpenAI CLIP,DALL-E)
软件缺陷的管理
Menu bar + status bar + toolbar ==pyqt5
LeetCode 50. Pow(x,n)
教你如何通过MCU配置S2E为TCP Server的工作模式
Oracle parsing XML with the same name
Arrays in JS
W5500上传温湿度到oneNET平台
Signal and slot mechanism ==pyqt5
阿里云技术专家秦隆:可靠性保障必备——云上如何进行混沌工程
LeetCode第303场周赛(20220724)
信号与槽机制==PYQT5
微信公众号开发 入手
Introduction to pl/sql, very detailed notes
知识图谱用于推荐系统问题(MVIN,KERL,CKAN,KRED,GAEAT)
Start with the development of wechat official account
程序员送给女孩子的精美礼物,H5立方体,唯美,精致,高清
A beautiful gift for girls from programmers, H5 cube, beautiful, exquisite, HD