当前位置:网站首页>【MATLAB】(四)MATLAB在线性代数中的应用
【MATLAB】(四)MATLAB在线性代数中的应用
2022-07-24 07:55:00 【记录无知岁月】
前期教程
概述
本篇博客主要用于记录MATLAB在线性代数中的应用。
一、矩阵
1 矩阵的创建
a. 直接创建
x1 = [1 2 3 4];
x2 = [5,6,7,8]; //创建行向量,空格或逗号进行分隔列
x3 = [2;3;1;4]; //创建列向量,用分号分隔行
x3 = [2 3 1 4]'; //转置的方法创建列向量
A = [1 2 3;4 5 6;7 8 9];
A = [1 2 3
4 5 6
7 8 9]; //直接创建矩阵,用分号或换行实现分行
b. 创建等距数组
等距数组即线性代数中的向量,这种特殊的向量一般用于循环遍历,和高级语言中数组概念差不多,故也称为数组

注意:用步长的方式可能最后一个数取不到(最后一个数和第一个数的差值不是步长整数倍);但用函数linspace得到的数组是包含首位,共n个数(步长自动计算好了),n可以省略,省略时默认为100。
c. 创建等比数组

和函数linspace一样,首位两个数都能取到,内部的等比已经计算好了。n值也可以省略,省略时默认为50。
d. 特殊矩阵
- A = [ ] : 创建一个空矩阵,空矩阵大小为0
- B = zeros(m, n) : 创建一个m行n列的零矩阵,如果只有一个参数n,则代表创建n阶方阵(下面的也类似),注意函数名有一个"s"!
- C = ones(m, n):创建一个m行n列的全为1的矩阵,注意函数名有一个"s"!
- D = eye(m, n):创建一个m行n列的单位矩阵,注意函数名没有"s"!
- E = rand(m, n): 创建一个m行n列的在 [0, 1] 内均匀分布的随机矩阵,如果需要创建其他范围的随机矩阵,可以用其他表达式乘以该矩阵。
- F = randn(m,n):创建一个m行n列的 标准正态分布(数据范围为[-1, 1]) 的矩阵。
e. 创建对角矩阵

f. Vandermonde矩阵
在MATLAB中创建Vandermonde矩阵的调用格式为:V=vander(C),其中C为一个向量(行向量或列向量无所谓),表示 1 , a 1 , a 2 , . . . , a n − 1 1, a_1,a_2,...,a_{n-1} 1,a1,a2,...,an−1,得到的矩阵的阶数为C的长度。需要注意的是,这里的Vandermonde矩阵是按行分的,而教材上是按列分的。看个例子就很容易明白了。
g. 符号矩阵的生成
在MATLAB中,输入一个表达式,实际代入计算的是它的近似值,即算出表达式的值并取一个近似。这一点从MATLAB中无法利用自然对数 e e e参与计算即可得知。而符号矩阵的作用就是使矩阵在计算时代入有理表达式,并在计算结果中保留有理表达式。如下图所示。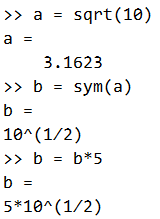
h. 多项式伴随矩阵
这里的伴随矩阵可不是线性代数中常用的 A ∗ A^* A∗,而是多项式的伴随矩阵,这个矩阵的特点在于它的特征值为该多项式的根。其计算原理如下图所示。
调用方式为A = compan(P),其中P为多项式的系数,从高次到低次。
i. 高阶矩阵的创建
比较少用,有缘再更新。
2 矩阵的修改
2.1 如何获取一个矩阵的大小
- [row, col] = size(A) %row为矩阵A的行数,col为A的列数
如果不需要某个参数,可以用 ~ 符号代替,表示参数缺省,如:
- [row, ~] = size(A) %表示只取矩阵A的行数row
这个在其他可以省略参数中的函数是一样的,比如只需要第1个参数和第3个参数,而省略第2个参数,则必须用 ~ 代替。否则就会把第3个参数当作第2个参数。
此外,还有其他一些获取矩阵的行列的方式:
- row = size(A, 1) %表示获取矩阵A的第一个参数,即行数
- col = size(A, 2) %表示获取矩阵A的第二个参数,即列数
- a = length(A) %返回值a = max{row, col}
2.2 矩阵中的元素操作



需要注意的是:矩阵、向量的索引都是小括号(),只有三维矩阵的索引和元胞数组(cell)是用 {},千万别搞混了!
2.3 一些特殊子矩阵的提取
- diag(A, k):表示将矩阵 A 的第 k 个对角线的元素提取组成列向量,若 k 省略 等价于k=0,表示主对角线元素。即该函数返回的是一个列向量。
- tril(A, k):表示提取矩阵A的第k个对角线以下的元素组成下三角矩阵,剩余部分补0,如果k省略,等价于k=0,即主对角线元素。该函数返回的是一个矩阵。
- triu(A, k):表示提取矩阵A的第k个对角线以上的元素组成上三角矩阵,剩余部分补0,如果k省略,等价于k=0,即主对角线元素。该函数返回的是一个矩阵。
- rot90(A):表示将矩阵A逆时针旋转90°,注意和转置运算区分开来!
- fliplr(A):表示将矩阵A左右翻转
- flipud(A):表示将矩阵A上下翻转
3 矩阵的运算
矩阵中常用的运算总结如下表:
注意区分带点运算符和不带点运算符!
另外,左除和右除的差别在于逆矩阵乘的位置,如果是 A − 1 B A^{-1}B A−1B,则是A\B(左除),等价于inv(A)*B,如果不是方阵,则相当于求 A X = B AX=B AX=B的解;
如果是 B A − 1 BA^{-1} BA−1,则是B/A(右除),等价于B*inv(A),如果不是方阵,等价于 X A = B XA=B XA=B的解。
二、线性相关与方程组
1 多项式
poly2sym( p ):输出以向量p为系数的多项式 p ( x ) p(x) p(x)。
polyval(p, a):返回多项式 p ( x ) p(x) p(x)当 x = a x=a x=a时的值。
roots( p ):返回多项式函数 p ( x ) = 0 p(x)=0 p(x)=0的所有复数根
conv(p1, p2):返回多项式 p 1 ( x ) p1(x) p1(x)和 p 2 ( x ) p2(x) p2(x)的乘积结果的系数
[a, b]=deconv(p1, p2):返回 p 1 ( x ) p1(x) p1(x)和 p 2 ( x ) p2(x) p2(x)的商式a和余式b的系数。
collect(f):对符号多项式f(syms x,即f(x) )进行合并同类项
expand(f):对符号多项式f进行展开
horner(f):对符号多项式f进行嵌套分解

factor(f):对符号多项式进行因式分解
[a, b, r] = residue(p, q):将有理分式 p ( x ) / q ( x ) p(x)/q(x) p(x)/q(x)分解为最简分式之和。看下面这个例子:

[p, q] = residue(a, b, r):将简单分式之和合并为一个有理分式,即上面那个表达式的逆运算。
2 向量组的相关性和极大无关组
- rank(A):求矩阵A的秩
- rref(A):将A化为行简化阶梯形矩阵,且每个主元都化为1,其他非该行主元都化为0。如下图所示。

这个指令的一个重要应用就是可以求矩阵的逆,即将单位阵和被求矩阵放一起再进行简化。
- [R, jb] = rref(A):输出A行变换后的阶梯型矩阵R和入选极大无关组的向量序号jb,因此jb是一个向量。如下图所示。

3 齐次线性方程组的解
- B=null(A):输出A的基础解系的标准正交基,即得到的矩阵B的所有列向量为 A X = 0 AX=0 AX=0的解向量,且这些解向量标准正交。
- B=null(A, ‘r’):输出A的基础解系,矩阵B的所有列向量为 A X = 0 AX=0 AX=0的解,且不进行正交化。
显而易见,比较常用的公式是后一个,即只求出基础解系。如果B矩阵为空矩阵,表示方程组 A X = 0 AX=0 AX=0只有零解,即A满秩。
4 非齐次线性方程组的解
首先补充一下理论知识:
这里只讨论有解的情况。
- 如果A为方阵,且A的行列式不为0,方程组有唯一解。
此时可以用两种方式求解:①X=inv(A)*b或X=A\b;②克莱姆法则求解;③linsolve(A,b),这个函数要求A必须是行满秩(A可以不是方阵)。 - 如果r(A)=r(A b)=r<n,方程组有无穷多解。
此时方程组的解由齐次通解和非齐次特解组成。这里介绍两种求特解的方式:①x0=pinv(A)*b,表示求A的广义逆矩阵,再与b向量相乘;②x0=A\b,用左除法求AX=b的解。需要注意的是,两种方式求得的解一般不同,前者求的是所有解中范数最小的一个,而后者求的是所有解中含零个数最多的一个。
三、特征值与二次型
1 求矩阵的特征值
- d=eig(A):仅计算A的特征值(以向量形式d存放)
- [V, D]=eig(A):其中,D为由特征值构成的对角矩阵,V为由特征向量作为列向量构成的矩阵,且使得 A V = V D AV=VD AV=VD成立。
这里有两个注意点:
1. 如果A不可相似对角化,仍然能够求出一个V矩阵,但是V矩阵不是满秩的。
2. 这里得到的V矩阵是已经单位化后的矩阵,如果A为对称矩阵,则V为正交矩阵。
- trace(A):计算矩阵A的迹。
2 二次型的标准化
- [P, T] = schur(A):A为二次型矩阵,即实对称矩阵;T为A的特征值所构成的对角矩阵;P为T对应的正交变换的正交矩阵,P的列向量为A的特征值所对应的特征向量。
经过实验发现,这个函数的作用和eig函数是一致的,即对于实对称矩阵来说,两个函数都能得到其正交变换的矩阵。
3 二次型正定的判断
一般判断二次型是否正定的方式是根据特征值,如果全为正数则为正定矩阵,但还有一种判断二次型是否正定的方法。
- [R, flag]=chol(A):如果A正定,则返回参数flag为0,如果不正定,flag为非零整数。

边栏推荐
- EZDML逆向工程导入数据库分析实操教程
- C language advanced part II Pointer
- Facing Tencent (actual combat) - Test Development - detailed explanation of interns (face experience)
- MySQL --- 子查询 - 标量子查询
- DevOps随笔
- When does MySQL use table locks and row locks?
- Arduino 超级省电之休眠模式用1节18650电池工作17年
- 【sklearn】tree.DecisionTreeClassifier
- About how to set colored fonts on the terminal
- Generative model and discriminant model
猜你喜欢

Image feature SIFT (scale invariant feature transform)

Detailed notes on pytoch building neural network
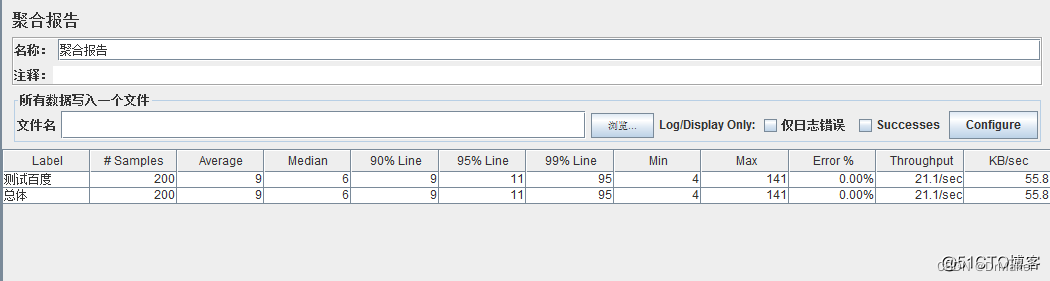
JMeter stress test index interpretation

从零开始C语言精讲篇3:函数

Appium doctor command error pit - resolved

QT | string generation QR code function

Why is knowledge base important? This is the best answer I've ever heard

Postman extracts the token parameter value in the response header and sets it as an environment variable, with code attached

Perceptron and multilayer neural network, back propagation and computational graph

Collection of linked list topics
随机推荐
Robot operation continuous learning thesis (1) original text reading and Translation -- primitive generation strategy learning without catastrophic forgetting in robot operation
2022-07-23:给定N件物品,每个物品有重量(w[i])、有价值(v[i]), 只能最多选两件商品,重量不超过bag,返回价值最大能是多少? N <= 10^5, w[i] <= 10^5, v
Image feature Harris corner detection
Stable TTL serial port rate supported by Arduino under different dominant frequencies
Hcip day 10 notes
Introduction to C language
Advanced part 5 of C language. Dynamic memory management
HCIP第十天笔记
What is NFT? An article to understand the concept of NFT
Basic operation of queue
Example of dictionary
Collection of sorting topics
mysql update 使用case when根据某一字段的值,更新另一字段的值
Facing Tencent (actual combat) - Test Development - detailed explanation of interns (face experience)
Error when using PIP: pip is configured with locations that requires tls/ssl
Decision tree - ID3, C4.5, cart
Intelligent robots and intelligent systems (Professor Zheng Zheng of Dalian University of Technology) -- 1. robots and mobile robots
Generate API documents using swagger2markup
MS SQL Server 2019 学习
Intelligent robots and intelligent systems (Professor Zhengzheng of Dalian University of Technology) -- 3. Industrial robots