【C】 Frog jumping steps and Hanoi Tower problem (recursion)

Blog home page : Xin Xiangrong
Series column :【 from 0 To 1,C Language learning 】
A short sentence : If you are in full bloom , Butterflies come ！
Blog description : Do what you can , Write every blog , Help yourself familiarize yourself with what you have learned , I also hope these contents can help some partners on the way of learning , If errors and deficiencies are found in the article , Also hope to leave a message in the comment area , We communicate progress together ！

Preface

This blog summarizes two classic problems in recursion , Frogs jump the steps and the tower of Hanoi , use C Language implementation ！

One . Frogs jump the steps

subject ：

A frog can jump up at a time 1 Stepped steps , You can jump on it 2 Stepped steps . Ask the frog to jump on one n How many jumps are there in the steps .

Their thinking ：

n=1, Jump a step , There's only one way to jump ;

n = 2, Jump a step first , Jump another step , Or just jump two steps , There are two ways to jump ;

n>2, The first time a frog jumps , There are two possibilities , Jump one step or two steps , Just add up the jump methods in these two cases , Use a function fib() To achieve a frog jump n How many jumps are there in the steps , So the result is Fib(n - 1) + Fib(n - 2).

Implement with recursion ,

Code ：

#include<stdio.h>
int Fib(int n)
{
    
	if (n <= 2)
	{
    
		return n;
	}
	if (n > 2)
	{
    
		return Fib(n - 1) + Fib(n - 2);
	}
}

int main()
{
    
	printf(" Enter the number of steps n = ");
	int n = 0;
	scanf("%d", &n);

	printf(" Yes %d Jump \n", Fib(n));
	return 0;
}

Running results ：

Two . Hanoi

Hanoi （Hanoi Tower）, Also known as the river tower , From an old Indian legend .

Vatican made three diamond pillars when he created the world , On a column, they are stacked from bottom to top in order of size 64 A golden disk .

Brahman ordered Brahman to rearrange the disc from below on another pillar in order of size .

And stipulate , anytime , You can't zoom in on a small disk , And you can only move one disc at a time between the three pillars . Ask how to operate ？

subject ：

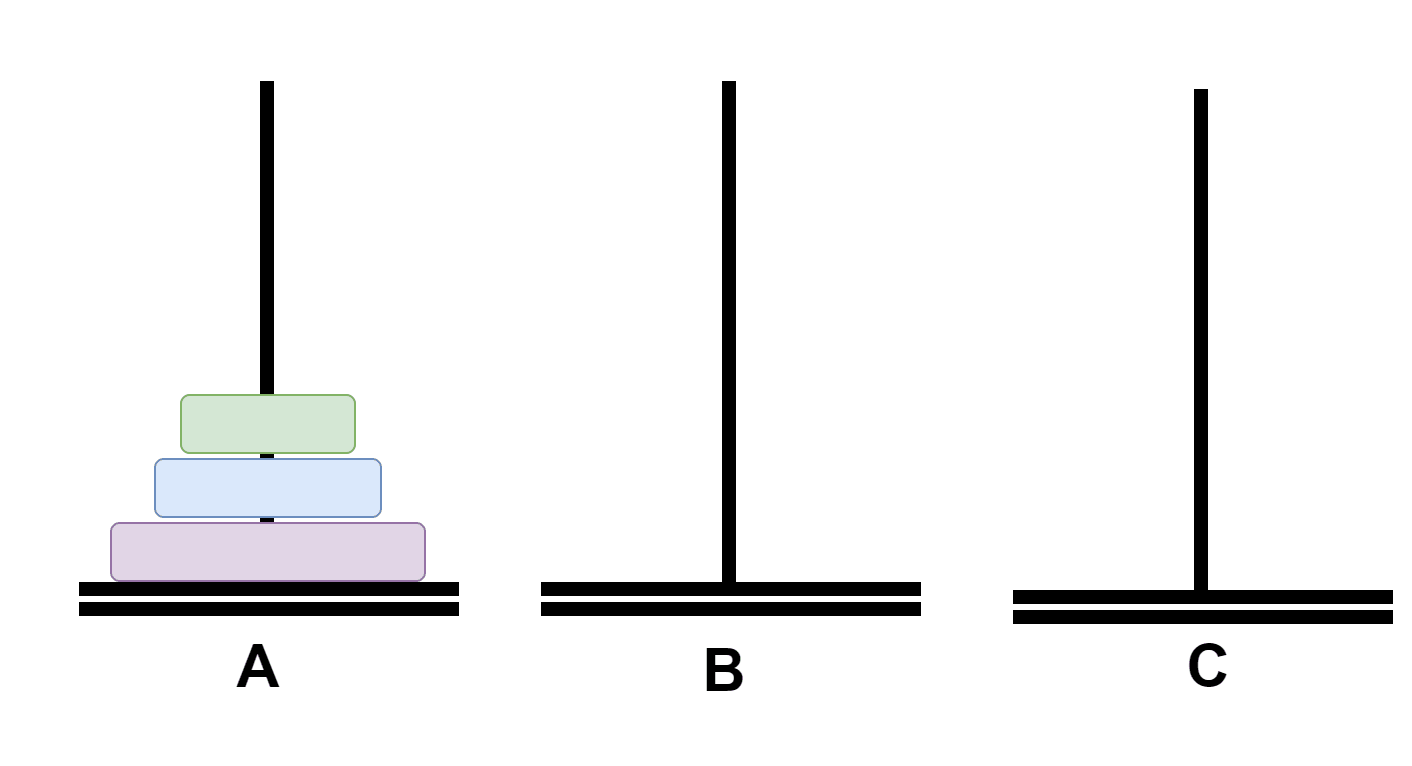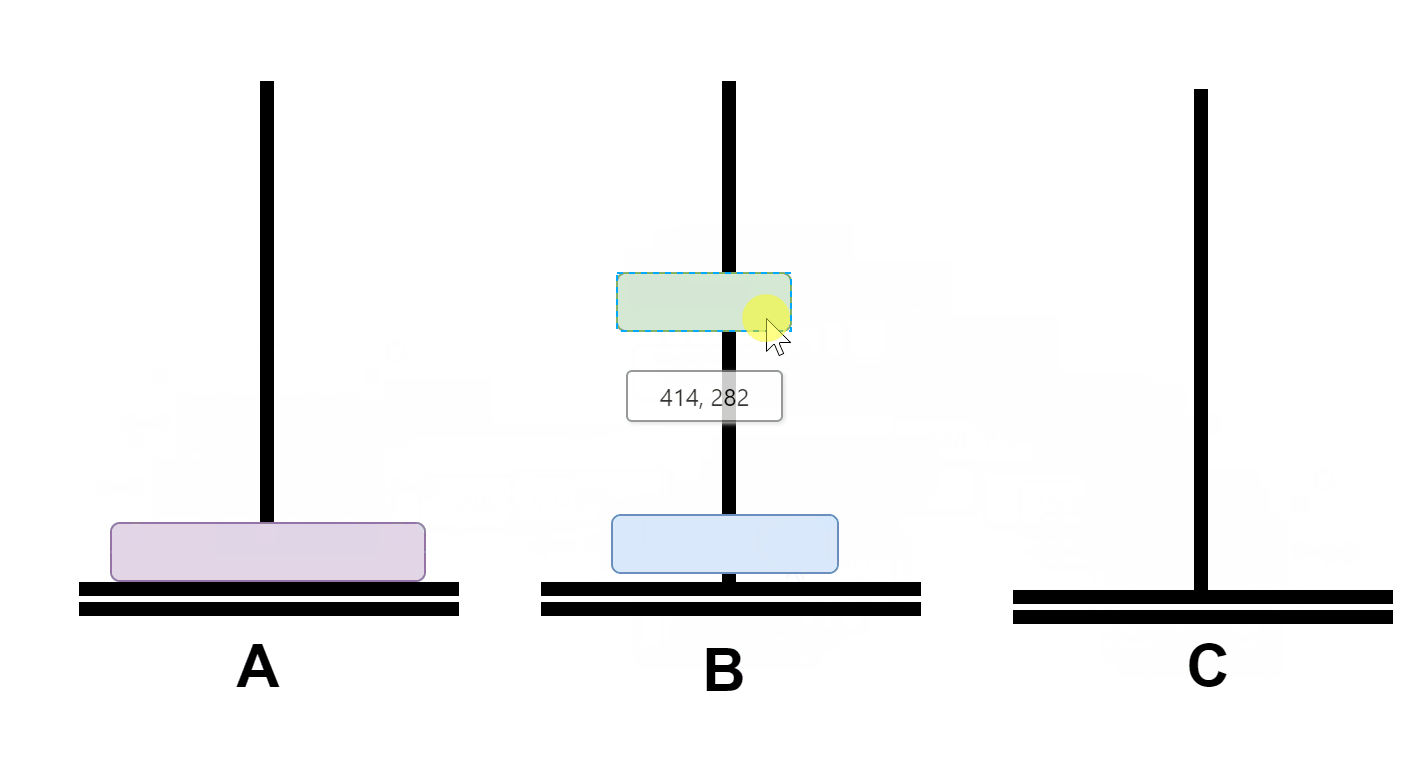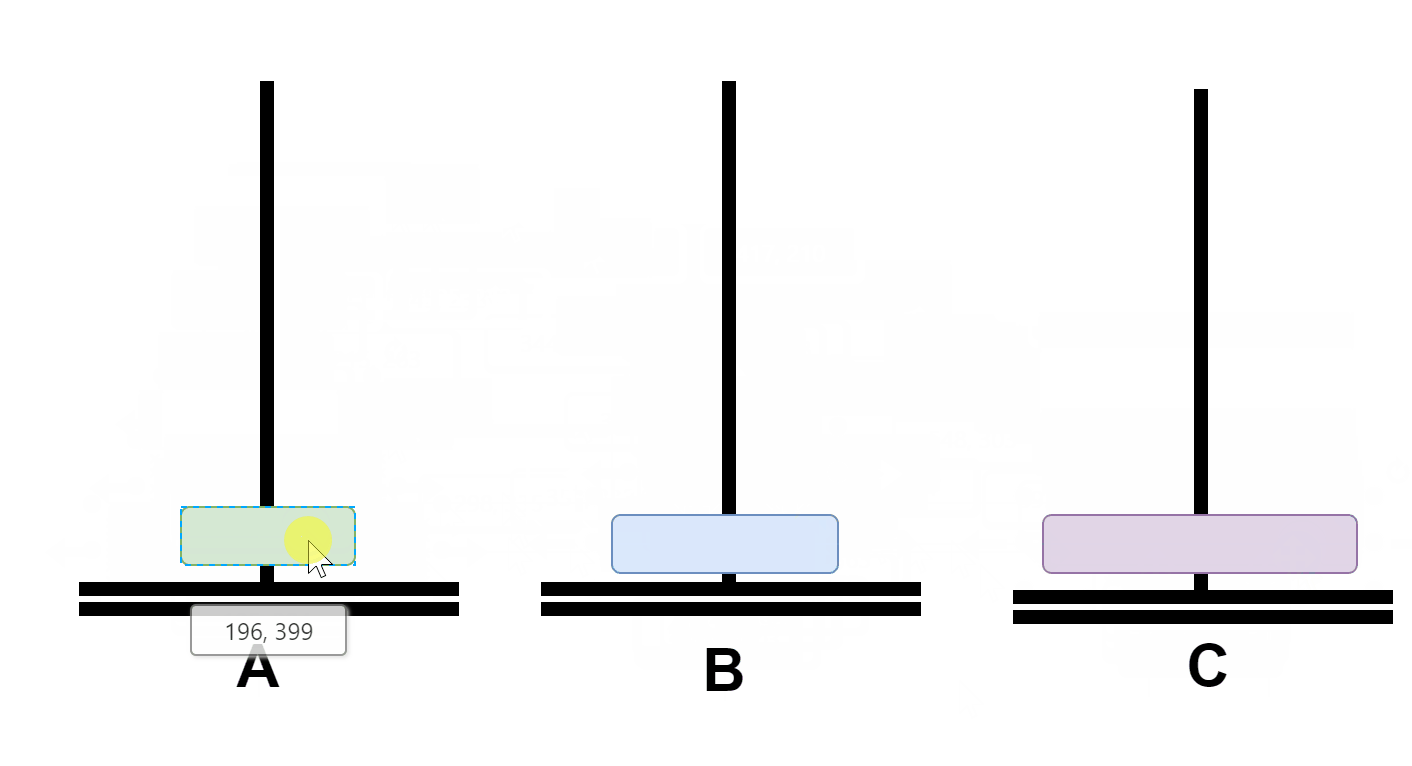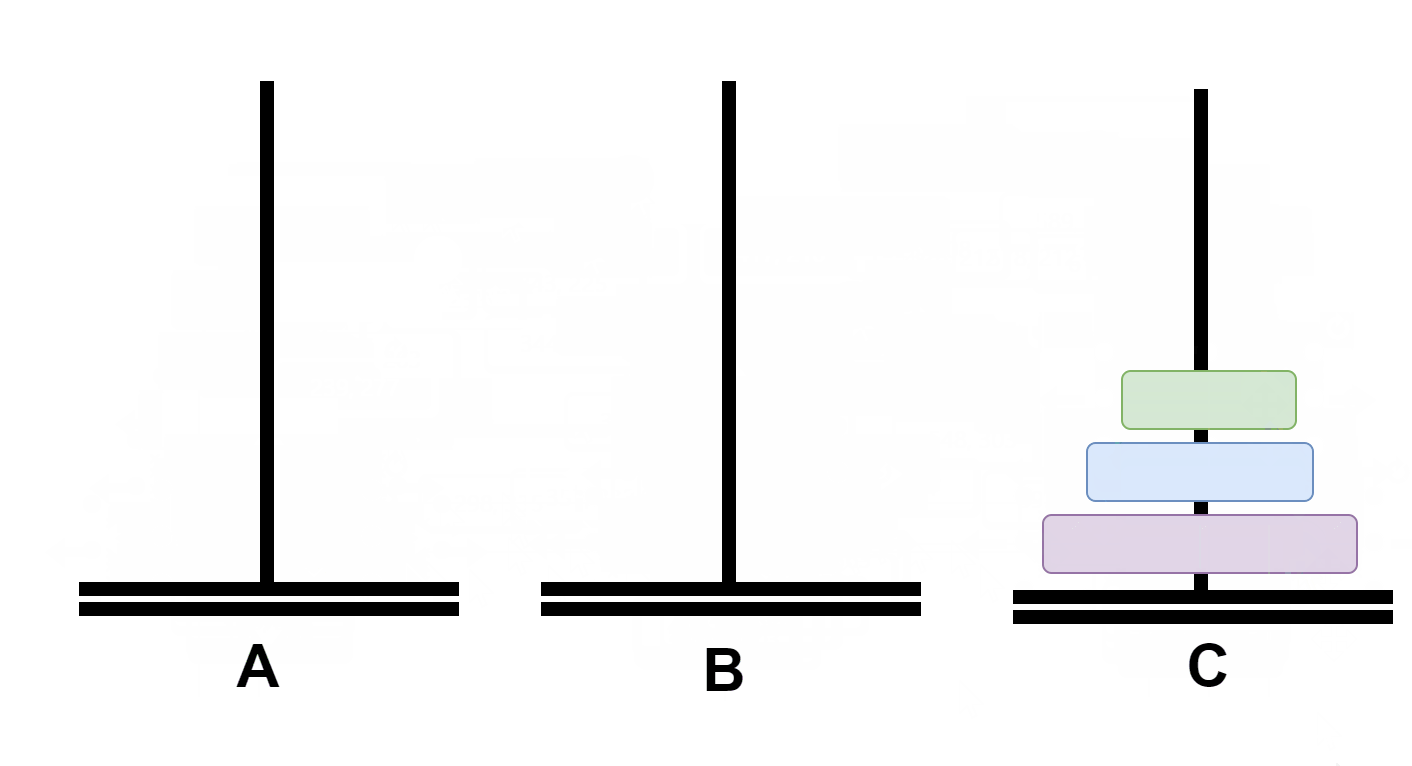
Here we implement such a process , Yes A、B、C Three pillars ,A There are... On the column n null , Will this n The plates move to C On the column , Use code to implement the movement process and calculate how many times to move ！

Their thinking ：

If n=3, Then the moving process of the three plates is as follows ：

First of all, will A The top two plates pass through C Move to B;

then A Plate on move to C;

then B The two plates on the go through A Move to C;

about n null , To pass it through B Put it in C On ;

We must first achieve A Put the bottom plate on C On , So let's first implement A above n-1 A plate passes through C Put it in B On , And then A Put the last plate on C On ;

then A Plate on move to C;

Then we need to realize that B The plate on the table passes through A Put it in C On , The implementation process is similar to the above , This procedure encapsulates a function for recursion .

For calculating the number of moves , It can also be implemented recursively , Ideas as follows ：

When n = 1 when , Times: 1;

When n > 1 when ,

1. The calculation will n-1 A plate from A adopt B Move to C The number of times
2. take A The last plate on the moves to C As a
3. take B On the plate (n-1 individual ) adopt A Move to C

You can also calculate the number of times according to the following rules ：

• Times: 2 ^ n - 1;

Code implementation ：

#include<stdio.h>
#include<math.h>

void Hannoi(int n, char A, char B, char C)
{
    
	if (1 == n)
	{
    
		printf("%c->%c ", A, C);
	}
	if (n > 1)
	{
    
		Hannoi(n - 1, A, C, B);
		printf("%c->%c ", A, C);
		Hannoi(n - 1, B, A, C);
	}

}

int Count_hannoi(int n)
{
    
	if (1 == n)
		return 1;
	if(n > 1)
	    return 2 * Count_hannoi(n - 1) + 1;
}

int main()
{
    
	printf(" Enter how many plates n = ");
	int n = 0;
	scanf("%d", &n);

	Hannoi(n, 'A', 'B', 'C');// Print the movement process 

	/*printf("\n Need to carry out %d Secondary mobility \n", (int)pow(2,n) - 1);*/  // Law method 
	printf("\n Need to carry out %d Secondary mobility \n", Count_hannoi(n));// Recursive method 
	return 0;
}

Running results ：

Conclusion

Dear friends , It's fate to see here , I hope my content can bring you a little help , If you can, support it for three times ！！！ Thank you for coming here , We can learn and communicate together , Progress together ！！！ come on. ！！！