当前位置:网站首页>Dynamic programming Backpack - 01 Backpack
Dynamic programming Backpack - 01 Backpack
2022-06-25 05:12:00 【Ability with desire】
Problem description
Yes N Items and capacity are W The backpack . The first i The weight of the item is w[i], The value is value[i], Each item can only be used once .
solve : Which items are loaded into the backpack with the greatest total value ?
1. Determine the state of
Define an array , Array elements represent the maximum value , One dimensional or two-dimensional array , Item quantity unknown a variable , Backpack capacity is gradually changed into a variable , Therefore, a two-dimensional array should be set :
f[i][j] For from 0 To i this i+1 The weight of the selected items in the items shall not exceed j Maximum total value of :
Based on the capacity of the backpack 4,
| goods | weight | value |
| goods 0 | 1 | 15 |
| goods 1 | 3 | 20 |
| goods 2 | 4 | 30 |
For example , Two dimensional array f[i][j] The structure is as follows :
| i j | 0 | 1 | 2 | 3 | 4 |
| goods 0 | |||||
| goods 1 | |||||
| goods 2 |
1) The last step :j<w[i]( The weight of the current item is larger than the capacity of the backpack , The backpack won't fit ),f[i][j] = f[i-1][j];
j>=w[i]( The weight of the current item is smaller than the capacity of the backpack ),f[i][j] = max(f[i-1][j],f[i-1][j-w[i]] + v[i]);
2) Sub problem : seek f[i-1][j],f[i-1][j-w[i]]+v[i]
2. Transfer equation
f[i][j] = max(f[i-1][j],f[i-1][j-w[i]]+v[i])
3. Initial and boundary conditions
1) Initial conditions : Be sure to and f Array match , Otherwise the recursion will become more and more chaotic
j = 0: Represents that the backpack capacity is 0, so f[i][0] = 0
i = 0:
if j >= w[0]( The capacity of the backpack is greater than 0 The weight of an item ): f[0][j] = v[0]
if j < w[0]( Backpack capacity is less than 0 The weight of an item ):f[0][j] = 0
so f[i][j] The array initialization is as follows :
| 0 | 1 | 2 | 3 | 4 | |
| goods 0 | 0 | 15 | 15 | 15 | 15 |
| goods 1 | 0 | ||||
| goods 2 | 0 |
f[i][j] After array initialization, other elements can be assigned at will
4. Computation order
Go through the items first , You can traverse the backpack weight first
I think it's easier to understand the backpack weight first ( ah , Maybe my brain is too stupid , Need to learn more )
Example
//#include<iostream>
//#include<malloc.h>
//#include<vector>
//#include<cstdbool>
#include<bits/stdc++.h>
using namespace std;
//LintCode;Coin Change
//3 Grow coins 2 element 5 element 7 element , Buy a Book 27 element
// How to pay with the least combination of coins , There is no need for the other party to pay f(x) Said to buy one 27 Yuan book to make up the least coin
/******66656565{2,5,7} *** 27*/
/*
int CoinChange(int A[], int m) {
int MAXN = 32001;
int **f = new int[m+1];
f[0] = 0;
int lenA = 0;
for (int i = 0; A[i] >= 0; i++) {
lenA++;
}
int i, j;
for (i = 1; i <= m; i++) { //1 2 3...m
f[i] = MAXN;
for ( j = 0; j < lenA; j++) { //2 5 7
if (i >= A[j] && A[i - A[j]] != MAXN) { // The required amount is greater than the face value and the current face value can make up the required amount
f[i] = f[i] < (f[i - A[j]] + 1) ? f[i] : (f[i - A[j]] + 1) ;
}
}
}
if (f[m] == MAXN) {
f[m] = -1;
}
return f[m];
}
*/
/*
LeetCode 62 Unique Paths
Given m That's ok n Column grid , There's a robot from the top left (0,0) set out , Each step can be down or down
How many different ways to get to the lower right corner
*/
int UniquePaths(int m, int n) {
std::vector<vector<int > > f(m); // That's ok
for (int i = 0; i < m; i++) { // Column
f[i].resize(n);
}
for (int i = 0; i < m; i++) { // That's ok
for (int j = 0; j < n; j++) {// Column
if (i == 0 || j == 0) {
f[i][j] = 1;
}
else {
f[i][j] = f[i - 1][j] + f[i][j - 1];
}
}
}
return f[m-1][n-1];
}
/*
LintCode116 Jump Game
Yes n The stones are in x The shaft 0,1,……,n-1 Location
A frog is in the stone 0, Want to jump to the stone n-1
If the frog is in the i On a stone , It can jump up to a distance to the right ai
Ask the frog if he can jump to the stone n-1
*/
bool JumpGame( int a[],int n) {
bool *f = new bool[n];
f[0] = true;
for (int i = 1; i < n; i++) {
f[i] = false;
for (int j = 0; j < i; j++) {
if (f[j]==true && j + a[j] >= i) {
f[i] = true;
break;
}
}
}
return f[n - 1];
}
/*
Fibonaci
*/
int Fibonacci(int n) {
int *f = new int[n];
f[0] = 0;
f[1] = 1;
for (int i = 2; i <= n; i++) {
f[i] = f[i - 1] + f[i - 2];
}
return f[n];
}
/*
01 knapsack
Yes n Weight and value are wi,vi The items . The total weight of these items shall not exceed W The items , Find the maximum value of the sum of values in all selection schemes .
Limiting conditions :
1 <= n <= 100
1 <= wi,vi <= 100
1 <= W <= 10000
*/
//…………………… weight …… value
int ZOBackPack(int w[],int v[],int W){
int n = 0;
for (int i = 0; w[i] > 0; i++) {
n++;
}
std::vector<vector<int > > f(n); // That's ok
for (int i = 0; i < n; i++) { // Column
f[i].resize(W+1);
}
for (int j = 0; j < W + 1; j++) { // weight
for (int i = 0; i < n; i++) { // goods
if (i==0||j == 0) {
if (j == 0) {
f[i][j] = 0;
}
if (i == 0 && j >= w[0]) {
f[i][j] = v[0];
}
if (i == 0 && j < w[0]) {
f[i][j] = 0;
}
}
else {
if (j < w[i]) {
f[i][j] = f[i - 1][j];
}
else {
f[i][j] = max(f[i - 1][j], f[i - 1][j - w[i]] + v[i]);
}
}
}
}
return f[n - 1][W];
}
int main(){
//Coinchange
/*
int A[] = { 2,5,7 };
int m = 27;
cout<<CoinChange(A,m);
*/
//UniquePaths
/*
int m = 8, n = 4;
cout << UniquePaths(m, n);
*/
//JumpGame
/*
int a[] = { 2,3,1,1,4 };
int lena = sizeof(a) / sizeof(int);
cout << boolalpha << JumpGame(a, lena) << endl;
*/
//Fibonacci
/*
cout << Fibonacci(8);
*/
//0-1 knapsack
int w[] = { 2,5,3,4,8 };
int v[] = { 20,40,15,5,10 };
int W = 15;
cout << ZOBackPack(w, v, W);
return 0;
}边栏推荐
- PHP calls map API
- buuctf(pwn)
- The construction and usage of wampserver framework
- 《QDebug 2022年6月》
- EL & JSTL (XIII)
- Creation and use of MySQL index
- Google Earth engine (GEE) - Global jrc/gsw1_ 1 / batch download of yearlyhistory dataset (China region)
- Professional things use professional people
- ORA-00800: soft external error
- CTFHub-rce
猜你喜欢

Difference between asemi high power FET and triode

Compatible with Internet Explorer

Working principle of asemi three-phase rectifier bridge
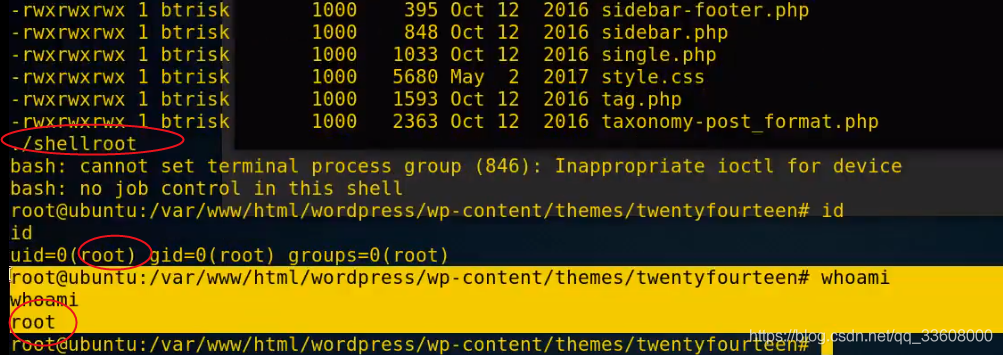
滲透測試-提權專題

In Net 6 using dotnet format formatting code

CSRF (Cross Site Request Forgery) &ssrf (server request forgery) (IV)

IronOCR 2022.1 Crack

Baidu ueeditor set toolbar initial value

How to install the blue lake plug-in to support Photoshop CC 2017

Two hours to take you into the software testing industry (with a full set of software testing learning routes)
随机推荐
Eyeshot Ultimate 2022 Crack By Xacker
Database overview
Svg code snippet of loading animation
魔法猪系统重装大师怎么使用
The print area becomes smaller after epplus copies the template
Detailed summary of flex layout
Professional things use professional people
Compatible with Internet Explorer
PHP calls map API
Virtual honeypot Honeyd installation and deployment
Detailed summary of position positioning
DOM document object model (I)
hr竟主动给这位测试小姐姐涨工资,她是怎么做到的?
H5 canvas drawing circle drawing fillet [detailed explanation]
How to make colleagues under the same LAN connect to their own MySQL database
Abuse unlimited authorization -- is your address safe?
Prototypical Networks for Few-shot Learning
Integrate CDN to create the ultimate service experience for customers!
What if the desktop computer is not connected to WiFi
Laravel Aurora push