当前位置:网站首页>[Huawei machine test] hj16 shopping list
[Huawei machine test] hj16 shopping list
2022-06-25 05:12:00 【Ability with desire】



Understand the meaning of the question
01 Backpack expansion , There is only one item , Each item has a price , Importance , A sign indicating the main part or accessory q,q=0, Indicates that the item is the main item ,q>0, Indicates that the item is an attachment , And now q The value is the number of the master .
Accessories must be bought by the buyer ,
Example above , The numbers of main parts are 1,4,5.
The problem is related to 01 Knapsack problem difference :
Difference one :01 The knapsack problem only considers the two situations of buying and not buying current items , But this question needs to consider 5 A purchase plan ,
namely 1) Don't buy the first i Item ,2) Only buy the main part ,3) Only buyer parts and accessories 1,4) Buyer parts and accessories 2,5) Buyer's piece and two accessories .
Difference two :01 The knapsack problem is to use v[i] To save the first i The value of an item , This problem requires a two-dimensional array v[i][0~3] Save the above main components 4 The price of the two schemes (2~5),w[i][0~3] preservation 4 The sum of the price and importance of the goods in the three schemes .
1. Determine the state of
An array , The array element represents the maximum sum of the product of item price and importance , The total amount of money is a variable , The number of items is a variable . Assume that each item is a primary item ( No effect on problem solving ), Each item has two attachments , A fictional subject , The fictitious accessory price and importance are 0.
f[i][j] preservation 1 To i this i+1 The total amount of money in this item does not exceed j( Can be equal to j) The maximum sum of the product of value and importance of goods .
v[i][0] Save the first i The price of an item ,w[i][0] Save the first i The product of the price of an item and its importance ,
v[i][1] Save the first i Items and their accessories 1 The sum of the prices of ,w[i][1] Save the first i Items and their accessories 1 The sum of the product of price and importance of ,
v[i][2] Save the first i Items and their accessories 2 The sum of the prices of ,w[i][2] Save the first i Items and their accessories 2 The sum of the product of price and importance of ,
v[i][3] Save the first i The sum of the prices of the items and their two accessories ,w[i][3] Save the first i The sum of the price and importance of an item and its two accessories .
Ruodi i Items are attachments , As mentioned above v[i][0~3] And w[i][0~3] Are all 0.
The last step :f[i][j] = max(
f[i-1][j] ,( Don't buy the first i Item )
f[i-1][j-w[i][0]]+v[i][0] ,( Buy a second i Item )
f[i-1][j - w[i][0]-w[i][1]]+v[i][0]+v[i][1] , ( Buy a second i Items and accessories 1)
f[i-1][j - w[i][0]-w[i][1]-w[i][2]]+v[i][0]+v[i][1]+v[i][2] ,( Buy a second i Items and accessories 2)
f[i-1][j-w[i][0]-w[i][1]-w[i][2]-w[i][3]]+v[i][0]+v[i][1]+v[i][3]).( Buy a second i Items and two accessories )
Sub problem :
Calculation
f[i-1][j]
f[i-1][j-w[i][0]]
f[i-1][j - w[i][0]-w[i][1]]
f[i-1][j - w[i][0]-w[i][1]-w[i][2]]
f[i-1][j-w[i][0]-w[i][1]-w[i][2]-w[i][3]]
2. State transition equation
f[i][j] = max(
f[i-1][j] ,( Don't buy the first i Item )
f[i-1][j-w[i][0]]+v[i][0] ,( Buy a second i Item )
f[i-1][j - w[i][0]-w[i][1]]+v[i][0]+v[i][1] , ( Buy a second i Items and accessories 1)
f[i-1][j - w[i][0]-w[i][1]-w[i][2]]+v[i][0]+v[i][1]+v[i][2] ,( Buy a second i Items and accessories 2)
f[i-1][j-w[i][0]-w[i][1]-w[i][2]-w[i][3]]+v[i][0]+v[i][1]+v[i][3]).( Buy a second i Items and two accessories )
3. Initialization and boundary conditions
f[0][……] = 0 ( I didn't choose any items , From the question, we know that the item variable is from 1 Start )
f[……][0] = 0 ( The total amount of money is 0)
4. Computation order
First traverse the total amount of money , Then traverse the items .
Example
#include <bits/stdc++.h>
using namespace std;
int v[61][3]; // Deposit Price
int w[61][3]; // Deposit ( Price * Importance )
int dp[61][32000];
int main(){
int N, m;
cin >> N >> m;
N /= 10;
for(int i=1; i<=m; i++){
int vv, p, q;
cin >> vv >> p >> q; // Price Importance Number
vv /= 10;
if(q){ // If it is an attachment
if(w[q][1]){ // The first attachment already exists , As a second attachment
v[q][2] = vv;
w[q][2] = vv*p;
}
else{ // No first attachment , As the first attachment
v[q][1] = vv;
w[q][1] = vv*p;
}
}
else{ // Main parts
v[i][0] = vv;
w[i][0] = vv*p;
}
}
// dp Dynamic programming
for(int j=1; j<=N; j++){
for(int i=1; i<=m; i++){
dp[i][j] = dp[i-1][j]; // 1、 Nothing
if(v[i][0] <= j){ // 2、 Only buy the main part
dp[i][j] = max(dp[i][j], dp[i-1][j-v[i][0]]+w[i][0]);
}
if(v[i][0] + v[i][1] <= j){ // 3、 Buyer parts and accessories 1
dp[i][j] = max(dp[i][j], dp[i-1][j-v[i][0]-v[i][1]]+w[i][0]+w[i][1]);
}
if(v[i][0] + v[i][2] <= j){ //4. Buyer parts and accessories 2
dp[i][j] = max(dp[i][j], dp[i-1][j-v[i][0]-v[i][2]]+w[i][0]+w[i][2]);
}
if(v[i][0] + v[i][1] + v[i][2] <= j){ // Buyer parts and accessories 1 And accessories 2
dp[i][j] = max(dp[i][j], dp[i-1][j-v[i][0]-v[i][1]-v[i][2]]+w[i][0]+w[i][1]+w[i][2]);
}
}
}
cout << dp[m][N]*10 << endl;
return 0;
}
边栏推荐
- Eyeshot Ultimate 2022 Crack By Xacker
- CopyPlugin Invalid Options options should be array ValidationError: CopyPlugin Invalid Options
- Understand JS high-order function and write a high-order function
- CSRF (Cross Site Request Forgery) &ssrf (server request forgery) (IV)
- Svg code snippet of loading animation
- XSS (cross site script attack) summary (II)
- Eyeshot 2022 Released
- Kotlin compose listens to the soft keyboard and clicks enter to submit the event
- Notes on non replacement elements in the line (padding, margin, and border)
- great! Auto like, I use pyautogui!
猜你喜欢
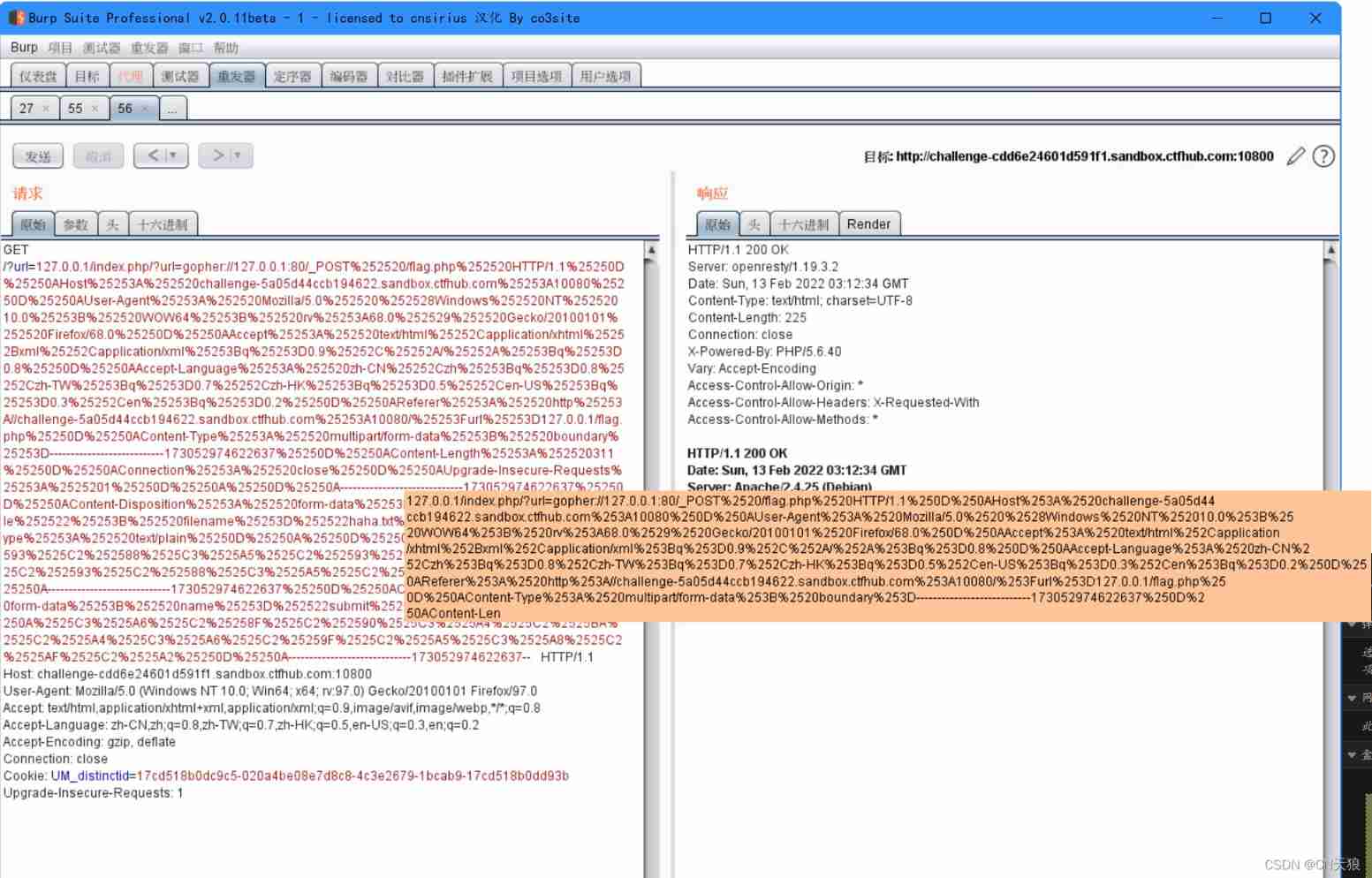
CTFHUB SSRF
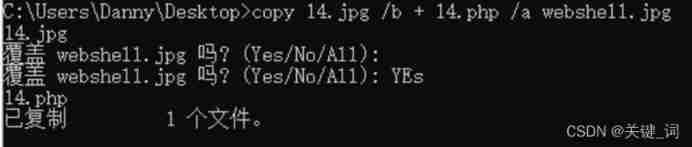
File upload vulnerability (III)

Kotlin compose listens to the soft keyboard and clicks enter to submit the event

Extend the toolbar of quill editor
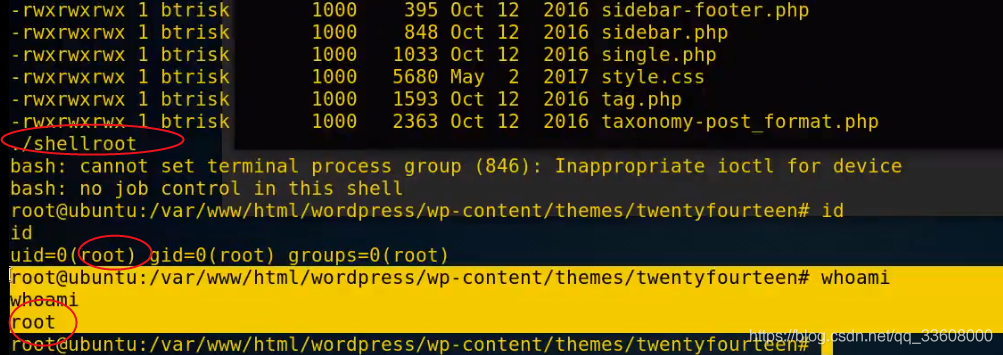
Essais de pénétration - sujets d'autorisation

In depth understanding of line height and vertical align

ThinkPHP 5 log management

win11蓝牙无法连接怎么办?win11蓝牙无法连接的解决方法

Specific operations for uploading pictures in PHP

基于SSH实现的学生成绩管理系统
随机推荐
Rce code execution & command execution (V)
DOM document object model (I)
Mysql interactive_ Timeout and wait_ Timeout differences
File upload vulnerability (III)
两小时带你进入软件测试行业风口(附全套软件测试学习路线)
The construction and usage of wampserver framework
Five simple data types of JS
MySQL prevents Chinese garbled code and solves the problem of Chinese garbled code
Edge loss interpretation
Conflict between v-mode and v-decorator in Ant Design
Laravel Aurora push
TeeChart Pro ActiveX 2022.1
Personalized Federated Learning with Moreau Envelopes
Svg code snippet of loading animation
Install pytorch through pip to solve the problem that torch cannot be used in jupyter notebook (modulenotfoundererror:no module named 'Torch').
A brief talk on media inquiry
[keil] GPIO output macro definition of aducm4050 official library
Redis (17)
Jason learning
Electric store stores data