世界坐标系、相机坐标系和图像坐标系的转换

坐标系转换

之前只是停留在会用的阶段，一直没去读懂计算的原理，今天通读了大佬的文章，写的言简意赅，感谢感谢~~特此记录一下，仅用作个人笔记

贴链接，十分感谢~
https://blog.csdn.net/weixin_44278406/article/details/112986651
https://blog.csdn.net/guyuealian/article/details/104184551

四个不同类型的坐标系

将三维物体转换成照片上的二维坐标，由四个坐标系进行转换。

1. 世界坐标系

世界坐标系是一个特殊坐标系，它建立了描述其他坐标系需要的参考框架。能够用世界坐标系描述其他坐标系的位置，而不能用更大的、外部的坐标系描述世界坐标系。从非技术意义上讲，世界坐标系建立的是我们所关心的最大坐标系，而不必真的是整个世界。
用$(X_w，Y_w，Z_w)$来表示，世界坐标系可通过旋转和平移得到相机坐标系。

2. 相机坐标系

以相机透镜的几何中心（光心）为原点，坐标系满足右手法则，用$(X_c，Y_c，Z_c)$来表示；相机光轴为坐标系的Z轴，X轴水平，Y轴竖直。

3. 图像物理坐标系

以CCD图像的中心为原点，坐标由 $(x,y)$ 表示，图像坐标系的单位，一般是毫米，坐标原点为相机光轴与成像平面的交点（一般情况下，这个交点是接近于图像的正中心）

CCD，英文全称：Charge coupled Device，中文全称：电荷耦合元件，可以称为CCD图像传感器。CCD是一种半导体器件，能够把光学影像转化为数字信号。 CCD上植入的微小光敏物质称作像素（Pixel）。一块CCD上包含的像素数越多，其提供的画面分辨率也就越高。

4. 图像像素坐标系

其实，当我们提及一个图像时，通常指的是图像的像素坐标系。像素坐标系的原点在左上角，并且单位为像素。

将图像坐标系的原点 $O_1$ ，转化到以 $O_0$ 为原点的坐标系中。使用的原因：

• 如果使用图像坐标系，单位mm，其实不太好衡量具体的图像，如果按照统一的像素标准，比较容易衡量图像的质量
• 如果使用图像坐标系，然后就有四个象限，这样会有正负数的问题，但是转换成像素坐标系后，都为整数。在后续的操作和运算中，都简化很多。

坐标转换

针孔模型（The basic pinhole model）。这种模型在数学上是三维空间到二维平面（image plane or focal plane）的中心投影，由一个 $3\times 4$ 投影矩阵$P=K[R|t]$来描述，$K$ 为相机内参（internal camera parameters），$[R|t]$为外参（external parameters）。

世界坐标 → 相机坐标（刚性变换）

$$\left[\begin{array}{c}{X}_c\\ Y_c\\ Z_c\\ 1\end{array}\right]=\left[\begin{array}{cc}R& t\\ & \\ 0_{1\ast 3}& 1\end{array}\right]\left[\begin{array}{c}{X}_w\\ Y_w\\ Z_w\\ 1\end{array}\right]$$
$X_c，Y_c，Z_c$代表相机坐标；$X_w，Y_w，Z_w$代表世界坐标；R代表正交单位旋转矩阵，t代表三维平移矢量。
根据旋转角度可以分别得三个方向上的旋转矩阵，而旋转矩阵即为他们的乘积：$R=R_x\ast R_y\ast R_z$
顺便记录一下三个旋转矩阵的公式，经常忘记。

绕$X$旋转$\theta$度

$$\left[\begin{array}{c}{X}_c\\ Y_c\\ Z_c\end{array}\right]=\left[\begin{array}{ccc}1& 0& 0\\ 0& cos\theta & sin\theta \\ 0& -sin\theta & cos\theta \end{array}\right]\left[\begin{array}{c}{X}_w\\ Y_w\\ Z_w\end{array}\right]=R_x\left[\begin{array}{c}{X}_w\\ Y_w\\ Z_w\end{array}\right]$$

绕$Y$轴旋转$\theta$度

$$\left[\begin{array}{c}{X}_c\\ Y_c\\ Z_c\end{array}\right]=\left[\begin{array}{ccc}cos\theta & 0& -sin\theta \\ 0& 1& 0\\ sin\theta & 0& cos\theta \end{array}\right]\left[\begin{array}{c}{X}_w\\ Y_w\\ Z_w\end{array}\right]=R_y\left[\begin{array}{c}{X}_w\\ Y_w\\ Z_w\end{array}\right]$$

绕$Z$轴旋转$\theta$度

$$\left[\begin{array}{c}{X}_c\\ Y_c\\ Z_c\end{array}\right]=\left[\begin{array}{ccc}cos\theta & sin\theta & 0\\ -sin\theta & cos\theta & 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}{X}_w\\ Y_w\\ Z_w\end{array}\right]=R_z\left[\begin{array}{c}{X}_w\\ Y_w\\ Z_w\end{array}\right]$$

相机坐标 → 图像坐标系（中心投影）

相机坐标系到图像坐标系是透视关系，利用相似三角形进行计算。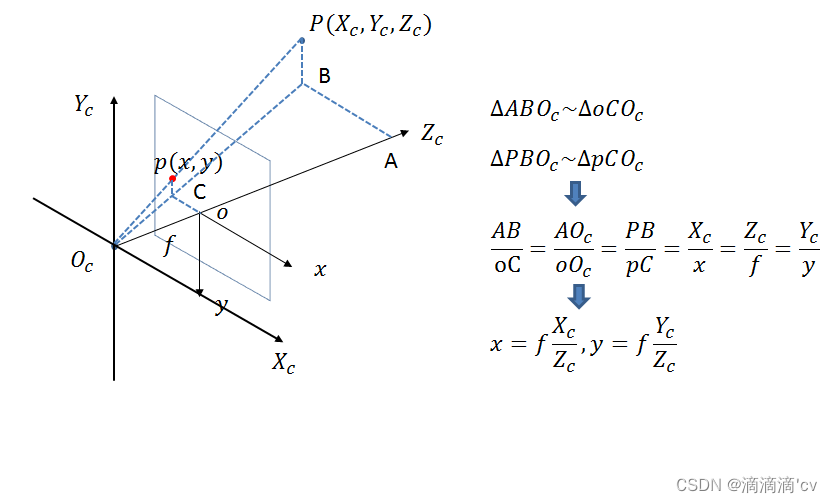

写成齐次坐标形式的矩阵相乘为
$$Zc\left[\begin{array}{c}x\\ y\\ 1\end{array}\right]=\left[\begin{array}{cccc}f& 0& 0& 0\\ 0& f& 0& 0\\ 0& 0& 1& 0\end{array}\right]\left[\begin{array}{c}{X}_c\\ Y_c\\ Z_c\\ 1\end{array}\right]=\left[\begin{array}{c}K|0\end{array}\right]\left[\begin{array}{c}{X}_c\\ Y_c\\ Z_c\\ 1\end{array}\right]$$
其中f代表焦距，即相机坐标系和图像坐标系在Z轴上的差。此时投影点p的单位还是mm，并不是pixel，不方便进行后续运算。

图像坐标系 → 像素坐标系（离散化）

像素坐标系的原点在左上角，并且单位为像素。像素坐标系和图像坐标系都在成像平面上，只是各自的原点和度量单位不一样。图像坐标系的原点为相机光轴与成像平面的交点，通常情况下是成像平面的中点或者叫principal point。图像坐标系的单位是mm，属于物理单位，而像素坐标系的单位是pixel，我们平常描述一个像素点都是几行几列。所以这二者之间的转换如下：其中dx和dy表示每一列和每一行分别代表多少mm，即1pixel=dx mm

$$Zc\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]=\left[\begin{array}{ccc}\frac{1}{d_x}& 0& u_0\\ 0& \frac{1}{d_y}& v_0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{cccc}f& 0& 0& 0\\ 0& f& 0& 0\\ 0& 0& 1& 0\end{array}\right]\left[\begin{array}{cc}R& t\\ & \\ 0_{1\ast 3}& 1\end{array}\right]\left[\begin{array}{c}{X}_w\\ Y_w\\ Z_w\\ 1\end{array}\right]$$
其中$\left[\begin{array}{ccc}\frac{1}{d_x}& 0& u_0\\ 0& \frac{1}{d_y}& v_0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{cccc}f& 0& 0& 0\\ 0& f& 0& 0\\ 0& 0& 1& 0\end{array}\right]$为相机内参矩阵，$\left[\begin{array}{cc}R& t\\ & \\ 0_{1\ast 3}& 1\end{array}\right]$为外参矩阵。相机标定就是为了求解这两个矩阵的参数。