《统计学习方法（第2版）》李航 第17章 潜在语义分析 LSA LSI 思维导图笔记 及 课后习题答案（步骤详细）第十七章

思维导图：

17.1

试将图17.1的例子进行潜在语义分析，并对结果进行观察。

import numpy as np

X = np.array([[2, 0, 0, 0],
              [0, 2, 0, 0],
              [0, 0, 1, 0],
              [0, 0, 2, 3],
              [0, 0, 0, 1],
              [1, 2, 2, 1]])

U, Sigma, VT = np.linalg.svd(X)
print(f'单词-话题矩阵为：\n{
      U[:, :4]}')
print(f'话题-文本矩阵为：\n{
      Sigma * VT}')

单词-话题矩阵为：
[[-7.84368672e-02 -2.84423033e-01  8.94427191e-01 -2.15138396e-01]
 [-1.56873734e-01 -5.68846066e-01 -4.47213595e-01 -4.30276793e-01]
 [-1.42622354e-01  1.37930417e-02 -1.25029761e-16  6.53519444e-01]
 [-7.28804669e-01  5.53499910e-01 -2.24565656e-16 -1.56161345e-01]
 [-1.47853320e-01  1.75304609e-01  8.49795536e-18 -4.87733411e-01]
 [-6.29190197e-01 -5.08166890e-01 -1.60733896e-16  2.81459486e-01]]
话题-文本矩阵为：
[[-7.86063931e-01 -9.66378217e-01 -1.27703091e+00 -7.78569971e-01]
 [-1.75211118e+00 -2.15402591e+00  7.59159661e-02  5.67438984e-01]
 [ 4.00432027e+00 -1.23071666e+00 -4.47996189e-16  6.41436023e-17]
 [-5.66440763e-01 -6.96375947e-01  1.53734473e+00 -6.74757960e-01]]

对于U矩阵，只保留了前4列，因为最终只有4个奇异值（话题）。另外，科学计数法有些不容易观察，我们保留2位小数看一下U矩阵：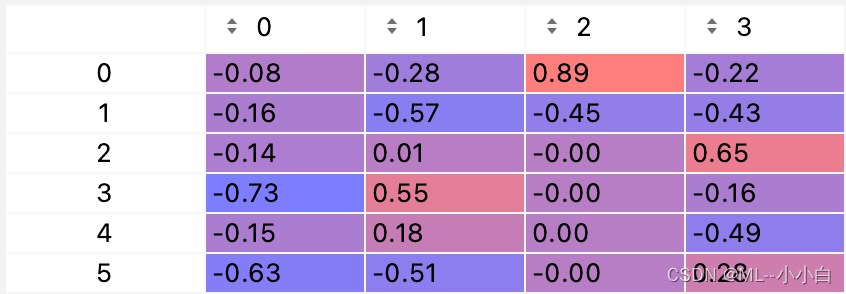

可以看到，第一列，比较重要的是第4和第6个单词，即apple和produce，猜测这个是关于苹果公司或苹果农产品有关的话题；
第二列，比较重要的是第2，4，6个单词，即aircraft，apple，produce，这个话题可能有一定的概率问题，鉴于aircraft，可能是苹果产品空运的话题;
第三列，最重要的是第一个单词，第二个相对重要，即airplane，airplane，猜测话题是航空相关的话题；
第四列，比较重要的是computer，fruit，aircraft，这个比较迷惑，可能说明数据不够多，分类仍然存在偏差，也可能这个奇异值或者说主成分已经不再重要。
接着看一下Sigma矩阵：

可以发现4个话题没有量级的差距，那么可能确实可以分成这四种话题而不是更少。
最后看一下VT矩阵：

分析其每列可知，第一个样本大概率是第3个话题，对应第三列的航空话题；
第二个样本大概率是第二个话题，可能涉及了苹果产品的运输，但是看实际情况可能并不如此；
第三个样本大概率是第四个话题，结合其在第一个话题的投影分量较大，猜测其是苹果产品的相关话题；
第四个样本大概率是第一个和第四个话题。
总之可以发现分析并不是那么准确。

17.2

给出损失函数是散度损失时的非负矩阵分解（潜在语义分析）的算法。

本题模仿书335页，算法17.1的方法即可，只不过把更新规则由平方损失的换为散度损失的即可。
输入：单词-文本矩阵$X\ge 0$, 文本集合的话题数$k$，最大迭代次数$t$；
输出：单词-话题矩阵$W$，话题-文本矩阵$H$。
(1)初始化：
$W\ge 0$, 并对$W$的每列进行归一化；
$H\ge 0$
(2)迭代：
对迭代次数由1到$t$执行以下步骤：
i. 更新$W$的元素，
$$W_{il}*W_{il}\frac{{\sum }_j{H}_{lj}{X}_{ij}/(WH{)}_{ij}}{{\sum }_j{W}_{lj}}$$
其中，$i$从1到$m$（单词数），$l$从1到$k$。
ii. 更新$H$的元素，
$$H_{lj}*H_{lj}\frac{{\sum }_i{W}_{il}{X}_{ij}/(WH{)}_{ij}}{{\sum }_i{W}_{il}}$$
其中，$j$从1到$n$（文本数），$l$从1到$k$。

17.3

给出潜在语义分析的两种算法的计算复杂度，包括奇异值分解法和非负矩阵的分解法。

首先，一般单词数$m$大于文本数$n$，对于奇异值分解算法，其复杂度为$O(m^3)$, 对于非负矩阵其复杂度为$O(t{m}^2)$

17.4

列出潜在语义分析与主成分分析的异同。

相同：
对于利用奇异值分解法进行的潜在语义分析LSA，其本质与主成分分析完全相同；
对于利用非负矩阵分解的LSA，其思想与截断奇异值分解相同。

不同：
对于利用奇异值分解法的LSA，在本书的样本为列，特征/单词为行的表示下，与PCA的过程一个是相差了PCA要进行数据的正规化（将原点放到数据均值位置，方差可归一可不归一），另外，PCA的SVD要将本书这种原始矩阵转置一下，因此PCA的SVD算法中的右奇异矩阵对应的是LSA的左奇异矩阵，还有一个不太重要的点就是PCA的SVD是样本PCA对于总体PCA的估计，利用了样本协方差是总体协方差的无偏估计，样本协方差出了刚才说的与LSA差一个转置外，还要有$\frac{1}{n-1}$的系数；
PCA的原始矩阵一般不是稀疏矩阵，LSA的矩阵一般为稀疏矩阵;
个人觉得，LSA可以尝试像PCA那样做数据的正规化，因为可能不同单词之间选成相同的scaling会有不太一样的结果，也许会更接近真实情况，但是没有实践过，有大佬测试过请留言告诉我，我挺好奇的；
LSA的非负矩阵分解NMF显然和SVD有算法上的不同，都是正值的好处是看着更好解释。