当前位置：网站首页>Explain AHP in human language (very detailed principle + simple tool implementation)

layer Time branch Analysis Law , namely Analytic Hierarchy Process(AHP) , Is an American operations research scientist Saaty On ２０ century ７０ s A subjective evaluation method of value assignment proposed in . Analytic hierarchy process decomposes the elements related to decision-making into objectives 、 Rules 、 Schemes, etc , On this basis, qualitative and quantitative analysis , It's a system 、 Simple and convenient 、 Flexible and effective decision-making methods .

This algorithm is a multi index comprehensive evaluation algorithm , Because the algorithm is simple 、 practical , Therefore, it is widely used in economics and management or in real life , It generally serves two purposes ：

Index weighting

Set weights for indicators , For example , For example, the decision to choose a tourist destination , Maybe we usually have the following 5 It's made up of three factors , But everyone （ subjective ） Different emphasis on factors ,ahp It can be realized without collecting data , Weight these indicators .

Quantitative scheme selection

It is also the decision to choose a tourist destination , Maybe we have some plans , For example, Suzhou and Hangzhou 、 peitaiho 、 The three schemes in Guilin , Analytic hierarchy process can synthesize the above 5 One factor , Calculate a quantitative score for these schemes , For example, Suzhou and Hangzhou 0.3 branch 、 peitaiho 0.35 branch 、 guilin 0.45 branch , In this way, according to the score , We can choose to get the most satisfying plan in our heart or experience .

Explain the function of analytic hierarchy process through the above , In life 、 In fact, there are a wide range of channels through which we can apply this model in our work , Especially those who need subjective decision-making 、 Or the decision-making scheme that needs to be judged by experience , for example ：

Buy a house （ Subjective decisions ）
Choose a tourist destination （ Subjective decisions ）
Evaluate the performance of employees （ Experience judgment ）
Choose a store address （ Experience judgment ）

2、AHP Analytic hierarchy process

The principle of analytic hierarchy process , Before analyzing a phenomenon or problem , First, the phenomenon or problem is decomposed into relevant factors according to their properties , And according to the relationship between them, a multi-level structure model is formed . Then through experience or experts , To judge and measure the relative importance of low-level factors to high-level factors , And according to the degree of importance, the weight ranking , And then we can make quantitative analysis and comparison . Hierarchy The core of the analysis method is to make the influencing factors hierarchical and digitized , It turns an abstract phenomenon or problem from difficult to Break it down easily , Easy to intuitively judge complex problems , And make decisions . Analytic hierarchy process (AHP) has the advantages of simplifying complex problems and simple calculation , It's widely used , Such as personnel quality evaluation 、 Comparison of multiple schemes 、 The evaluation of scientific and technological achievements and the evaluation of work results have been applied in many fields and aspects .

In short , Analytic hierarchy process is to decompose a decision-making event into target layer （ For example, choose a tourist destination ）, Criterion layer （ Factors that influence decision making , For example, scenery 、 traffic 、 Expenses, etc ） And the scheme layer （ It refers to the scheme , For example, go to Guangzhou 、 Guilin and other places for tourism ）.

During the application of analytic hierarchy process , The general steps mainly include four . The first step is to build a hierarchical model . The second step is to construct a judgment matrix , The third step is hierarchical single sorting and its consistency test , This step is to weight the indicators , The fourth step is the overall hierarchical sorting and its consistency test , If there is no decision-making level , It is usually possible to omit .

PS： The meaning of consistency check is used to determine whether there is a logical problem in the constructed judgment matrix , For example A、B、C Build a judgment matrix , If it is determined that A amount to B by 3（A Than B A little important ）,A amount to C by 1/3（C Than A A little important ）, In judging B amount to C when , According to the above logic , should C Than B important , If we are building a judgment matrix , It is incorrectly filled in as B amount to C by 3（B Than C A little important ）, Then you make a logical mistake .

2.1 Build a hierarchical evaluation model

seeing the name of a thing one thinks of its function , In this hierarchical evaluation model , We need to identify the target layer of the entire decision event 、 Criterion layer 、 Scheme layer

among ,

Target layer ： The best choice of tourist destination

Criterion layer ： scenery 、 cost 、 live 、 diet 、 Journey

Scheme layer ： Xi'an 、 yunnan 、 Tibet 、 qinghai

Need to pay attention to when , If the criterion layer has multiple layers , For example, as shown in the figure below , And so on .

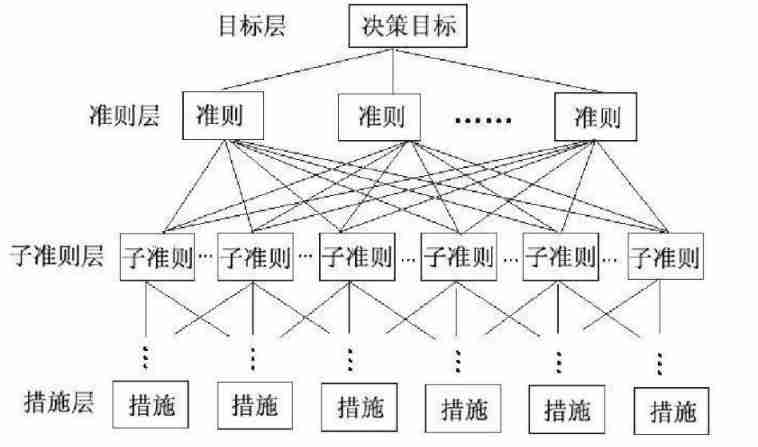
2.2 Construct judgment matrix

The construction of the judgment matrix is based on the comparison between the elements , And determine the weight of each criterion layer to the target layer .

In short , That is to judge the indicators of the criterion layer by two , Usually we use Santy Of 1-9 The scaling method gives .

For the criteria layer A, We can build a

among A The elements in meet ：

In short , For example, for the criteria layer ： scenery 、 cost 、 live 、 diet 、 Journey , We can build such a 5*5 Judgment matrix of ：

The diagonal line is the judgment of each indicator , For example, for 【 scenery 】 And 【 scenery 】, Its importance is 1, Because it must be the comparison between the indicators themselves 1：1. For the second row, the first column , That is to say 【 cost 】 And 【 scenery 】 contrast , Maybe I think 【 cost 】 Than 【 scenery 】 Obviously important , Then it can be marked as 5

Then the judgment matrix becomes ：

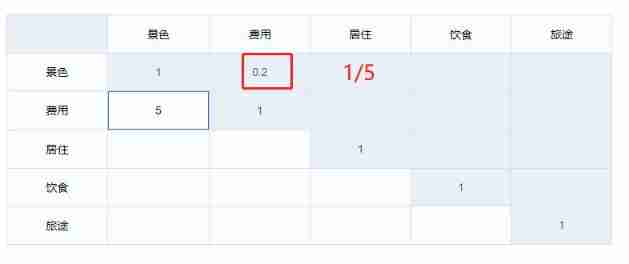
And so on , Until a complete judgment matrix is built .

2.3 Hierarchical single sorting and consistency checking

Here are the general descriptions in the literature ：

step1： Hierarchical single sort

Hierarchical single sorting refers to comparing all the elements in the current layer with one element in the previous layer , And carry out hierarchical sorting , Arrange in order of importance , The specific calculation can be based on the judgment matrix A Conduct , In the calculation, ensure that it can meet AW=𝜆𝑚𝑎𝑥𝑊 The eigenvalue and eigenvector conditions of . Here it is ,A The largest characteristic root of is λmax, Corresponding λmax The normalized eigenvector of is W,𝑤𝑖 by W Components of , It refers to the weight , It corresponds to the sorting of its corresponding element list . Use the judgment matrix to calculate the factors 𝑎𝑖𝑗 The weight of the target layer （ Weight coefficient ）.

The weight vector （W） And the biggest feature （λmax） The calculation steps of （ Square root method or sum method ） As shown in the following table ：

step2： Solve the maximum eigenvalue and CI value

set up n The order judgment matrix is B, Then the maximum characteristic root can be obtained by the following method 𝜆𝑚𝑎𝑥:

BW=λW

among ,W yes B Eigenvector of . In analytic hierarchy process , We use the following consistency indicators CI To test the consistency index of judgment （Consistency Index）：

C.I.=0 Indicates that the judgment matrix is completely consistent ,C.I. The bigger it is , The more inconsistent the judgment matrix is .

step3： according to CI、RI Value solving CR value , Determine whether the consistency is passed

Satty simulation 1000 Random consistency index obtained for times R.I. Value table （ The following table Shown ）：

When C.R.<0.1 when , Indicates the judgment matrix A The degree of consistency is considered to be within the allowable range , At this point, you can use A To calculate the weight vector ; if C.R.≥0.1, Then the judgment matrix should be considered A Amendment .

Now let me say something ：

2.3.1 Hierarchical single sort

In short , Hierarchical single sorting is based on our judgment matrix , Solve the weight of each index .

For example, we are now 2.2 The judgment matrix of criterion layer is constructed A as follows ：

Then we can calculate its weight （ The weight vector ）, There are two ways , One is the square root method , One is the harmony method .

The weight calculated by the square root method is as follows ：

Calculate the product of each row m Power , Get one m Dimension vector

namely ：

（2） Normalize the vector as a weight vector , That is, the weight

namely ：

The weight calculated by the sum method is as follows ：

step1： First standardize each column of the matrix

step2： Sum the standardized elements by line

step3： Standardize the summation results

For example, this picture shows ：

2.3.2 Solve the maximum eigenvalue and CI value

above , Get the weight matrix , The maximum characteristic root can be calculated , The formula is ：

among n Is the number of dimensions , For example, the constructed judgment matrix is ： scenery 、 cost 、 live 、 diet 、 During the journey ,n=5;

AW by ： Judgment matrix * Standardized weights , Then press the cumulative value by row .

Judgment matrix A by ：

indicators

scenery

cost

live

diet

Journey

scenery

0.3333

cost

0.2

0.25

0.1667

live

0.2

diet

Journey

0.125

0.5

0.3333

0.1667

Weight after standardization W by ：

scenery

cost

live

diet

Journey

0.3104

0.0591

0.1157

0.4716

0.0432

among A*W by ：

indicators

scenery

cost

live

diet

Journey

scenery

0.3104

0.2955

0.5785

0.15718428

0.3456

cost

0.06208

0.0591

0.028925

0.07861572

0.0864

live

0.06208

0.2364

0.1157

0.09432

0.1296

diet

0.9312

0.3546

0.5785

0.4716

0.2592

Journey

0.0388

0.02955

0.03856281

0.07861572

0.0432

AW：

λmax：

AW1/W1+AW2/W2+AW3/W3+···+AWn/Wn=x

Maximum eigenvalue λmax=x/ Matrix order =5.416

Maximum eigenvalue λmax After solving it ,C.I Value is much better ,

according to C.I Value formula ,λmax=5.416,n=5, Substituting to obtain C.I value =0.1042

2.3.3 according to CI、RI Value solving CR value , Determine whether the consistency is passed .

The meaning of consistency check is used to determine whether there is a logical problem in the constructed judgment matrix , For example A、B、C Build a judgment matrix , If it is determined that A amount to B by 3（A Than B A little important ）,A amount to C by 1/3（C Than A A little important ）, In judging B amount to C when , According to the above logic , should C Than B important , If we are building a judgment matrix , It is incorrectly filled in as B amount to C by 3（B Than C A little important ）, Then you make a logical mistake ;

RI The value can be known by looking up the table , This is Satty simulation 1000 Random consistency index obtained for times R.I. Value table （ The following table Shown ）：

And our matrix is 5 rank （ Number of criteria layer factors ）, The order of the matrix is 5 Time corresponds to RI The value is 1.12, Generation into the formula ：

You can get C.R. The value is 0.1042/1.12=0.093.

therefore C.R.=0.093<0.1 when , Indicates the judgment matrix A The degree of consistency is considered to be within the allowable range , At this point, you can use A To calculate the weight vector ; if C.R.≥0.1, It shows that we made a logical error when building the judgment matrix ,

for example B matrix , Let's assume that when we compare the third row and the second column in pairs , Filled in 1/5, At this time, the consistency test cannot be passed , Because it made a logical mistake , According to the second row and the first column , You can see that Shanghai is a little more important than Guangzhou , According to the first column of the third row , We can see that Beijing is more important than Guangzhou , So according to logic ： Shanghai > Guangzhou , Beijing 》 Guangzhou , So Beijing should be > Shanghai , But we filled in 1/5, That is, Beijing is less important than Shanghai , So there is a logical error , This is the time , We need to evaluate the judgment matrix A Amendment , Revised to Beijing > Shanghai .

thus , We have completed the hierarchical single sorting and consistency test , By using the analytic hierarchy process, we can only use it here , It is used to weight the indicator , If we have a solution layer , It is necessary to do the total hierarchy sorting and its consistency test .

2.4 Hierarchical total ranking and consistency test

Here are the general descriptions in the literature ：

Calculate all factors at a certain level for the highest level （ Target layer ） Weight of relative importance , It is called hierarchical scheduling order . The process is carried out from the highest level to the lowest level ：

set up B layer 𝐵1 ,𝐵2 ⋯ ,𝐵𝑛 On the upper （A layer ） Medium factor 𝐴𝑗（𝑗 = 1,2, ⋯ ,𝑚） Hierarchical sorting of The consistency index is 𝐶𝐼𝑗, The random consistency index is 𝑅𝐼𝑗 , Then the consistency ratio of the total hierarchy sorting is ：

When 𝐶𝑅 < 0.1 when , It is considered that the hierarchical total ranking passes the consistency test , Otherwise, it is necessary to readjust the judgment matrix Element value of . Here we are , According to the lowest level （ Decision makers ） To make the final decision .

Now let me say something ：

The total order of levels , In fact, the scheme is scored by the method of type level single sorting .

For example , We according to the 2.3 Hierarchical single sorting , Now make sure A1~A5 The weight for

scenery

cost

live

diet

Journey

0.3104

0.0591

0.1157

0.4716

0.0432

Now I want to calculate the solution B1: The score of Suzhou and Hangzhou , But we don't know the score of the scenery of Suzhou and Hangzhou , So what should we do ？

similar 2.3 Hierarchical single sorting , For the scenery factor , We can build a 3*3 Matrix , As shown below ：

Compare the scenery of each scheme in pairs by sorting the hierarchical list , We can get Suzhou and Hangzhou 、 peitaiho 、 The weight of Guilin , Then this weight can be used as Suzhou Hangzhou 、 peitaiho 、 Guilin's score in scenery .

By analogy , We have constructed Suzhou and Hangzhou 、 peitaiho 、 Guilin's score matrix on the scenery A1, Score matrix on cost A2, Score matrix on residence A3, Score matrix on diet A4, Score matrix on the journey A5：

The calculated score is ：

PS： Consistency test is required for all the above judgment matrices .

So for the scheme B1（ Suhang ）, Its total score is ：

The score of Suzhou and Hangzhou in the scenery * The weight of the scenery + The score of Suzhou and Hangzhou on expenses * Weight of expenses + The score of Suzhou and Hangzhou in living * The weight of residence + The score of Suzhou and Hangzhou in diet * Weight of diet + The score of Suzhou and Hangzhou on the journey * The weight of the journey =0.5954*0.3104+0.819*0.0591+0.4286*0.1157+0.6337*0.4716+0.1667*0.0432=0.5889

And so on , The scheme can be calculated B2（ peitaiho ） by

0.2764*0.3104+0.2363*0.0591+0.4286*0.1157+0.1919*0.4716+0.1667*0.0432=0.2471

programme B3（ guilin ）：

0.1283*0.3104+0.6817*0.0591+0.1429*0.1157+0.1744*0.4716+0.6667*0.0432=0.2077

Therefore, Suzhou and Hangzhou scored the highest , Choose to go to Suzhou and Hangzhou .

3、 Case and tool implementation

3.1 The most important factor in traveling

The function here is actually to find the factor weight , Therefore, only the hierarchical single sort is calculated , There is no solution layer , That is, there is no need for total hierarchical sorting .

3.1.1 Using tools

SPSSPRO—>【 Analytic hierarchy process （AHP Simplified edition )】

3.1.2 Case operation

step1： choice 【 Analytic hierarchy process （AHP Simplified edition )】;

step2： Select the judgment matrix hierarchy

step3： Set the judgment matrix （ The judgement matrix is a symmetric matrix ）

step4： Click on 【 To analyze 】, Complete the operation .

3.1.3 Analysis results interpretation

The following generated results are from SPSSPRO The analysis results of the software are exported , I mentioned the calculation method in Chapter 2 , The analysis results are listed below .

Output results 1： Build judgment matrix results

This is the judgment matrix filled in the previous operation page

Output results 2：AHP Analytic hierarchy process results

The weight calculation results based on the square root method show , The weight score of the scenery is 0.2657, The weighted score of expenses is 0.4212, The weighted score of residence is 0.0657, The weight score of diet is 0.1067, The weight score of the journey is 0.1407, The maximum characteristic root is 5.1352,CI by 0.0338.

Output results 3： Consistency test results

The results show that , The maximum characteristic root is 5.1352, according to RI The corresponding table is found RI The value is 1.11, therefore CR=CI/RI=

0.0305<0.1, Pass the one-time inspection , Explain the rationality of the weight determination method , There is no need to modify the judgment matrix .

It should be noted that , there RI The value adopts the more recognized in recent years Franek and Kresta (2014) The way , No longer use satty Methods .

3.1.4 Summary

from 3.1.3 You can know , The most important factor in traveling is the cost , Its weight score is 0.4212, This result is very subjective , Because the decision to choose a tourist destination is a very subjective decision , It's like selling a house , The decision-making factors that affect buying a house are also very subjective , Everyone has his own steelyard , But if it's a shop , For example, the location of milk tea shop , Then we can find experienced people to judge by two , Or collect more expert judgments , averaging , For subjective things , When there are more people with the same ideas , Then there is an objective fact .

3.2 Choose the best place to travel

The function here is to calculate the quantitative score of the scheme , Therefore, it is necessary to sort the calculation hierarchy of the criteria layer , Sort the scheme layer .

3.2.1 Using tools

SPSSPRO—>【 Analytic hierarchy process （AHP pro )】

3.2.2 Case operation

Step1： Choose analytic hierarchy process （AHP pro ）;

Step2： Choose to build a decision model ;

Step3： Input the constructed evaluation index ;

Step4： Enter the final solution ;

Step5： Confirm to proceed to the next step of index scoring ;

Step6： Enter the importance value of pairwise comparison between indicators ;

Step7： Input the importance evaluation of the corresponding evaluation values of different schemes ;

3.1.3 Analysis results interpretation

The following generated results are from SPSSPRO The analysis results of the software are exported , I mentioned the calculation method in Chapter 2 , The analysis results are listed below .

Output results 1： Program score

After single sorting based on indicator level and total sorting based on scheme level , Beidaihe is the best choice for the tourist destination 、 The second is Guilin . The quantitative score of Beidaihe is 1.435, It is nearly twice as high as the second Guilin .

Output results 2： Hierarchical decision model

The figure is visible , The two most important determinants are the scenery and cost of the tourist destination , And diet 、 Living conditions are low weighted .

Output results 3： The judgment matrix summarizes the results

Here are the eigenvectors and weights ,CR Less than 0.1, Consistency check passed , Analytic hierarchy process results are valid .

Output results 4： Summary results of scheme level judgment matrix

The above table shows the weight calculation results of the scheme layer of the analytic hierarchy process （ That is, total hierarchy sorting ）, A judgment matrix with the number of leaf node indexes is constructed to analyze the weight of each index , By showing the consistency test results , It is used to judge whether there is a logical problem of constructing the judgment matrix in the scheme layer weight matrix . Because the score of the upper level node can be based on the score of its child nodes * Weight calculation results in , Therefore, when constructing the scheme level judgment matrix , Only leaf nodes are built , namely N A leaf node is built N A judgment matrix , It is used to compare the two situations , Get the score of the scheme layer for a leaf node ;

You can see , The scores of the schemes meet the consistency test .

3.2.4 Summary

from 3.2.3 You can know , Beidaihe is the best choice for the tourist destination , Its quantitative score is 1.435, Scheme level judgment matrix of hierarchical total ranking , It is done without data , In reality , If we are faced with choosing a tourist destination 、 Choose to rent 、 Choosing to buy a house is a subjective decision , Then the hierarchical total sorting can be adopted , If it is extended to store location 、 Express cabinet selection 、 The selection of activity plan and other things that need objective decision-making , We can actually optimize in two ways ：

Based on most experienced people , Adopt hierarchical total sorting , Calculating mean , Turn subjectivity into objectivity （ This is usually combined with a method called Delphi method , It is also called expert investigation method ）
Do hierarchical general sorting based on real data , For example, store selection , Suppose there is a traffic indicator , Real indicators can be used to quantify the solution .

原网站

版权声明
本文为[Halosec_ Wei]所创，转载请带上原文链接，感谢
https://yzsam.com/2022/02/202202200535108207.html