当前位置:网站首页>(heavy chain dissection) Magic Tree
(heavy chain dissection) Magic Tree
2022-07-23 14:35:00 【Soup key】
[SHOI2012] Magic Tree ( The whole process is annotation )
Background
SHOI2012 D2T3
Title Description
Harry Potter Learned a new kind of magic : You can change the number of fruits on the tree . Filled with joy, he found a huge fruit tree , To test his new spell .
This fruit tree shares N N N Nodes , Where nodes 0 0 0 Root node , Every node u u u My father is recorded as f a [ u ] fa[u] fa[u], Guaranteed f a [ u ] < u fa[u] < u fa[u]<u . At the beginning , The fruit on this fruit tree is Dumbledore Removed by magic , So there is no fruit on each node of the fruit tree ( namely 0 0 0 A fruit ).
Unfortunately ,Harry You don't learn your spells well , You can only increase the number of fruits on the nodes of a path in the tree by a certain number . in other words ,Harry Magic can be described as :A u v d . Indicates that a point will be selected u u u and v v v Add the number of fruits of all nodes on the path between d d d.
Next , To facilitate inspection Harry Is your magic successful , You need to tell him some information about fruit trees in the process of releasing magic :Q u. Indicates... In the current tree , With a little u u u In the subtree of the root , How many fruits are there in total ?
Input format
First line a positive integer N ( 1 ≤ N ≤ 100000 ) N (1 \leq N \leq 100000) N(1≤N≤100000), Represents the total number of nodes in the fruit tree , Node to 0 , 1 , … , N − 1 0,1,\dots,N - 1 0,1,…,N−1 label , 0 0 0 It must represent the root node .
Next N − 1 N - 1 N−1 That's ok , Two integers per line a , b ( 0 ≤ a < b < N ) a,b (0 \leq a < b < N) a,b(0≤a<b<N), Express a a a yes b b b Father .
Next is a positive integer Q ( 1 ≤ Q ≤ 100000 ) Q(1 \leq Q \leq 100000) Q(1≤Q≤100000), Expressing common ownership Q Q Q operations .
Follow behind Q Q Q That's ok , Each line is one of the following two :
A u v d, It means that you will u u u To v v v The number of fruits of all nodes on the path plus d d d. Guarantee 0 ≤ u , v < N , 0 < d < 100000 0 \leq u,v < N,0 < d < 100000 0≤u,v<N,0<d<100000Q u, Means to ask with u u u The total number of fruits in the subtree of the root , Note that includes u u u Of itself .
Output format
For all Q operation , Output the answers to the questions in turn , Each row of a . The answer may exceed 2 32 2^{32} 232 , But not more than 1 0 15 10^{15} 1015 .
Examples #1
The sample input #1
4
0 1
1 2
2 3
4
A 1 3 1
Q 0
Q 1
Q 2
Sample output #1
3
3
2
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=2e5+10;
int head[N],cnt;
int fa[N],size[N],deep[N],son[N],top[N],dfsxu[N],id[N],k;
//fa[i] node i Parent node size[i] With i Is the total number of nodes in the subtree of the root
//deep[i] node i The depth of the son[i] node i My dear son
//top[i] node i The top element of the heavy chain
//dfsxu Initial value of each point id Time stamp
int n,v[N],m,r,ss[N];
struct stu{
int l,r,sum,lz;
}tree[N*4];
struct stuu{
int to,nt;
}ed[N*2];
void add(int u,int v){
// Chain forward star edge
ed[cnt]=stuu{
v,head[u]};
head[u]=cnt++;
}
void dfs1(int u,int f){
//u Is the current node ,f Is the parent node of the current node ; initialization 1
fa[u]=f;//u The parent of the node is f
deep[u]=deep[f]+1;// depth +1
size[u]=1;
int maxsize=-1;// It is a temporary variable to judge whether it is a heavy son
for(int i=head[u];i!=-1;i=ed[i].nt){
// Traverse all the sons , Keep updating and find your son
int v=ed[i].to;
if(v==f) continue;// My father must have skipped it directly
dfs1(v,u);// Depth traversal , The current node becomes the parent node , The found son becomes the current node and continues to traverse
size[u]+=size[v];// After traversal , Let the size of the current node plus the size of the son
if(size[v]>maxsize){
// If the size of the son is larger than the temporary variable
maxsize=size[v];// Just assign it to a temporary variable
son[u]=v;// Change the heavy son of the current node
}
}
}
void dfs2(int u,int t){
// initialization 2
id[u]=++k;// Each node is timestamped
top[u]=t;// node u The top of the heavy chain is t
if(!son[u]) return;// If there is no heavy son, there will be no son. Go back directly
dfs2(son[u],t);// Continue to walk towards your son
for(int i=head[u];i!=-1;i=ed[i].nt){
int v =ed[i].to;
if(v==fa[u]||v==son[u]) continue;// If it is a parent node or a duplicate son, skip directly
dfs2(v,v);// Some heavy chains start with light sons and go down , The top is light son
}
}
void pushup(int u){
// Update up
tree[u].sum=tree[u<<1].sum+tree[u<<1|1].sum;// The interval sum of the left and right sub segments is fed back to the top
}
void pushdown(int u){
// Update down , take lazy Mark push down
if(tree[u].lz){
tree[u<<1].sum+=tree[u].lz*(tree[u<<1].r-tree[u<<1].l+1);
tree[u<<1|1].sum+=tree[u].lz*(tree[u<<1|1].r-tree[u<<1|1].l+1);
tree[u<<1].lz+=tree[u].lz;
tree[u<<1|1].lz+=tree[u].lz;
tree[u].lz=0;
}
}
void build(int l,int r,int u){
// Build up trees
tree[u].l=l,tree[u].r=r;
if(l==r){
// Reach the leaf node , Update and return
return ;
}// Otherwise, this node represents more than one point , It also has two sons
int mid=(l+r)>>1;
build(l,mid,u<<1);// Recursive left subtree
build(mid+1,r,u<<1|1);// Recursive right subtree
pushup(u);// to update
}
void update(int l,int r,int u,int b){
if(l<=tree[u].l&&tree[u].r<=r){
// Included as a subinterval , Then make an overall modification , Don't go further
tree[u].sum+=b*(tree[u].r-tree[u].l+1);
tree[u].lz+=b;
return ;
}// Otherwise, it is staggered , You need to continue to go deeper into the lower sub interval
pushdown(u);// Update down
int mid=(tree[u].l+tree[u].r)>>1;
if(l<=mid) update(l,r,u<<1,b);// Recursive left subtree
if(r>=mid+1) update(l,r,u<<1|1,b);// Recursive right subtree
pushup(u);// to update
}
int query(int l,int r,int u){
if(l<=tree[u].l&&tree[u].r<=r){
// Included as a subinterval , Then make an overall modification , Don't go further
return tree[u].sum;
}// Otherwise, it is staggered , You need to continue to go deeper into the lower sub interval
int k=0;
int mid=(tree[u].l+tree[u].r)>>1;// Binary search
pushdown(u);// Update down
if(l<=mid) k+=query(l,r,u<<1);// Part of the inquiry is under the jurisdiction of the left son
if(r>=mid+1) k+=query(l,r,u<<1|1);// Part of it is within the scope of the right son
return k;
}
void updatecc(int a,int b,int c){
while(top[a]!=top[b]){
// look for LCA: When x,y Not in the same heavy chain , Compare x,y The depth of the head of the heavy chain
if(deep[top[a]]<deep[top[b]]) swap(a,b);// Ensure deeper
update(id[top[a]],id[a],1,c);// By climbing lca Every time you jump the chain head to modify or query the interval
a=fa[top[a]];// The deeper one jumps along the heavy chain to the father at the head of the chain
}
if(deep[a]>deep[b]) swap(a,b);
update(id[a],id[b],1,c);
}
signed main(){
memset(head,-1,sizeof(head));
cin>>n;
int u,v,p;
for(int i=1;i<n;i++){
scanf("%lld%lld",&u,&v);
++u,++v;
add(u,v),add(v,u);
}
dfs1(1,0),dfs2(1,1);
build(1,n,1);
cin>>m;
while(m--){
char k;
cin>>k;
if(k=='A'){
scanf("%lld%lld%lld",&u,&v,&p);
++u,++v;
updatecc(u,v,p);
}
else{
scanf("%lld",&p);
p++;
printf("%lld\n",query(id[p],id[p]+size[p]-1,1));
}
}
return 0;
}
边栏推荐
- Surrounded Regions
- 581. 最短无序连续子数组
- STM32 output sine wave +cubemx configuration +hal Library
- Le shell a besoin de connaître les commandes
- [baiqihang] Niuer education helps colleges and universities visit enterprises, expand posts and promote employment
- The shell needs to know the commands when running
- 对象使用过程中背后调用了哪些方法
- webstrom ERROR in [eslint] ESLint is not a constructor
- Pagehepler lost the pit of the original SQL order by condition
- 152. 乘积最大子数组
猜你喜欢

【C語言】猜數字小遊戲+關機小程序

关于flex布局justify-content:space-around最后一个不对齐的解决方法和为什么这样子解决是讨论
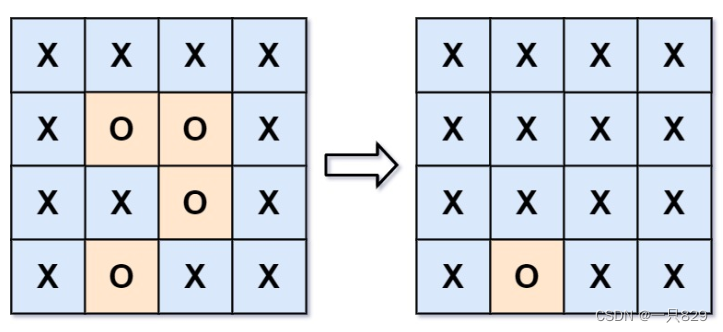
Surrounded Regions

How can manual testing turn to automated testing? Byte 5 years of automation experience talk about
建议思源笔记能够兼容第三方同步盘

uni-app知识点和项目上遇到的问题和解决办法的记录

4. 寻找两个正序数组的中位数
![[download attached] several scripts commonly used in penetration testing that are worth collecting](/img/01/3b74c5ab4168059827230578753be5.png)
[download attached] several scripts commonly used in penetration testing that are worth collecting

【FLink】FLink Hash collision on user-specified ID “opt“. Most likely cause is a non-unique ID

Several hole filling methods of point cloud (mesh) (1)
随机推荐
Towhee 每周模型
右键新建txt,新建文本文件不见了,通过添加注册表就可以解决,找来找去办法解决不了的终极办法
打家劫舍!
C language implements memcpy and memmove
Cool code rain dynamic background registration page
C language implements StrCmp, strstr, strcat, strcpy
【WinForm】关于截图识别数字并计算的桌面程序实现方案
求岛屿最大面积--深度优先搜索(染色法)
Pacific Atlantic current problem
koa框架的使用
[C language] number guessing game + shutdown applet
手机股票开户风险性大吗,安全吗?
Chapitre 2 requête de base et tri
FFmpeg 2 - ffplay、ffprobe、ffmpeg 命令使用
几种点云(网格)孔洞填充方法(1)
因为资源限制,导致namenode启动失败,报错unable to create new native thread
LabVIEW运行中改变Chart的历史长度
全志F1C100S/F1C200S学习笔记(13)——LVGL移植
Stream stream is used for classification display.
Sword finger offer19 regular expression
