当前位置:网站首页>Calculate Euclidean distance and cosine similarity
Calculate Euclidean distance and cosine similarity
2022-06-23 05:18:00 【Dream painter】
In this paper, Python Calculate Euclidean distance and cosine similarity . For cosine similarity, we need to use Euclidean distance , Let's first introduce the European distance .
Euclidean distance
Euclidean distance identifies the distance between two vectors , The calculation formula is as follows :
Euclidean distance = Σ ( A i − B i ) 2 \sqrt{Σ(A_i-B_i)^2} Σ(Ai−Bi)2
python Calculate the Euclidean distance , have access to numpy.linalg.norm function :
# Import package
import numpy as np
from numpy.linalg import norm
# Define vector
a = np.array([2, 6, 7, 7, 5, 13, 14, 17, 11, 8])
b = np.array([3, 5, 5, 3, 7, 12, 13, 19, 22, 7])
# Calculate the Euclidean distance between two vectors
norm(a-b)
# 12.409673645990857
The output shows that the Euclidean distance between the two vectors is :12.409673645990857
If two vectors are not equal in length , Function generates a warning :
import numpy as np
from numpy.linalg import norm
a = np.array([2, 6, 7, 7, 5, 13, 14])
b = np.array([3, 5, 5, 3, 7, 12, 13, 19, 22, 7])
norm(a-b)
# Generate error messages , Can't broadcast
# ValueError: operands could not be broadcast together with shapes (7,) (10,)
You can also calculate the Euclidean distance for the columns of the data frame :
import pandas as pd
import numpy as np
from numpy.linalg import norm
# Define the data frame
df = pd.DataFrame({'points': [25, 12, 15, 14, 19, 23, 25, 29],
'assists': [5, 7, 7, 9, 12, 9, 9, 4],
'rebounds': [11, 8, 10, 6, 6, 5, 9, 12]})
# stay 'points' and 'assists' Calculate Euclidean distance between two columns
norm(df['points'] - df['assists'])
# 40.496913462633174
Cosine similarity
Cosine similarity measures the difference between two vectors by the cosine of the angle between two vectors in vector space . The closer the cosine is to 1, It shows that the closer the angle between two vectors is 0 degree , Then the more similar the two vectors are .
The calculation formula is as follows :
Cosine similarity = Σ A i B i / ( Σ A i 2 Σ B i 2 ) { ΣA_iB_i /(\sqrt{ΣA_i^2}\sqrt{ΣB_i^2}}) ΣAiBi/(ΣAi2ΣBi2)
How to use NumPy The library calculates the cosine similarity of two vectors .
from numpy import dot
from numpy.linalg import norm
# Define an array
a = [23, 34, 44, 45, 42, 27, 33, 34]
b = [17, 18, 22, 26, 26, 29, 31, 30]
# Calculate cosine similarity
cos_sim = dot(a, b)/(norm(a)*norm(b))
cos_sim
0.965195008357566
norm Function to calculate the Euclidean distance ,dot Calculate the dot product of the vector .
You can also use this method for longer array lengths :
import numpy as np
from numpy import dot
from numpy.linalg import norm
# Define an array
a = np.random.randint(10, size=100)
b = np.random.randint(10, size=100)
# Calculate cosine similarity
cos_sim = dot(a, b)/(norm(a)*norm(b))
cos_sim
0.7340201613960431
The last thing to say is , If the length is inconsistent, an error will still be reported .
边栏推荐
- Rtklib new version 2.4.3 B34 test comparison
- VMware network connection error unit network service not found
- Unity中,如何在【编辑器】和【运行时】状态下读写一个ScriptableObject对象
- 使用teqcplot对teqc 质量分析结果进行可视化展示
- 微信小程序:拼图工具箱
- Architecture à trois niveaux MVC
- laravel8实现图片验证码
- Three methods of GNSS velocity calculation
- 飞桨框架v2.3发布高可复用算子库PHI!重构开发范式,降本增效
- 渗透测试基础 | 附带测试点、测试场景
猜你喜欢

Image noise reduction denoise AI

UnityShader入门精要——Unity中的渲染优化技术(四)

What is the average annual salary of an outsourced tester who has worked for 5-8 years?

大環境不好難找工作?三面阿裏,幸好做足了准備,已拿offer

Drag and drop拖放框架
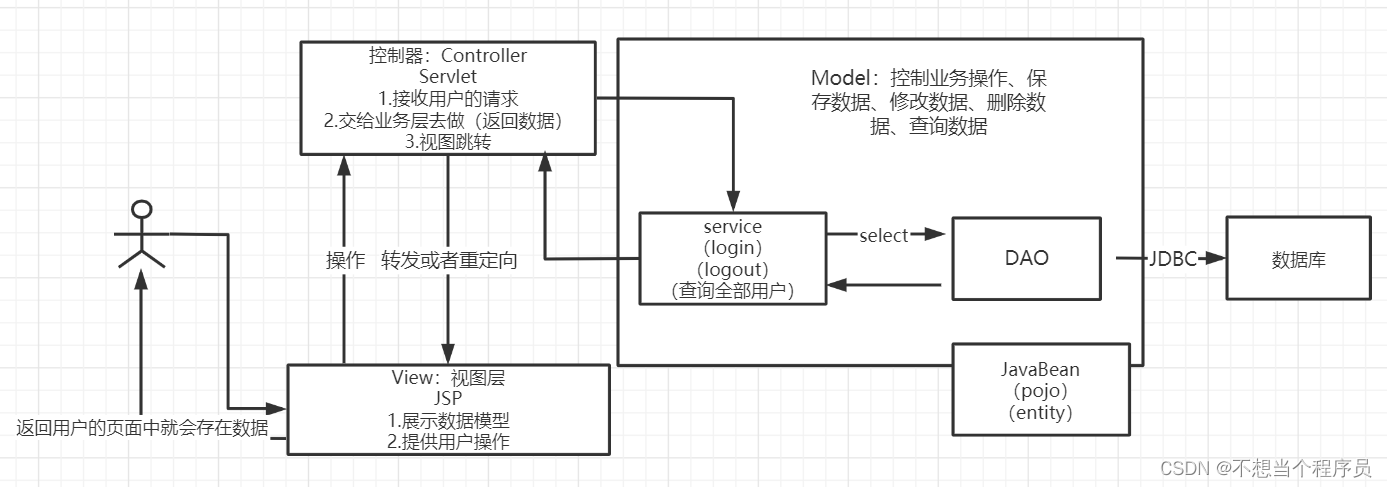
MVC三层架构
三层架构实验

AMS:startActivity桌面启动应用

Web 应用程序安全测试指南

The propeller framework v2.3 releases the highly reusable operator library Phi! Restructure development paradigm to reduce cost and increase efficiency
随机推荐
Swiftui 2.0 course notes Chapter 5
超越芯片和AI,硬科技资本为什么越来越“硬核”?
三层架构实验
UnityShader入门精要——Unity中的渲染优化技术(四)
Visual display of TEQC quality analysis results using teqcplot
AMS:startActivity桌面启动应用
Jetpack Compose 从开门到入门之 MenuBar桌面菜单(Desktop Menu)
985测试工程师被吊打,学历和经验到底谁更重要?
This markdown artifact will be charged!
单行或多行文本溢出,省略号代替
Course design C for freshmen -- clothing management system
飞桨框架v2.3发布高可复用算子库PHI!重构开发范式,降本增效
Unity中,如何在【编辑器】和【运行时】状态下读写一个ScriptableObject对象
The technological advance of new employees? Journey
JDBC调用存储过程、MySQL触发器
Event日志关键字:EventLogTags.logtags
Servlet self study notes
Hcip fifth operation
Complete the primary school project in 3 days, and teach you to complete the weather broadcast system hand in hand!
A compiler related bug in rtklib2.4.3 B34