Interpretation of bilstm-crf in NER forward_ algorithm

If you have any doubts about the following , You may need to read what I wrote in my previous article BiLSTM-CRF Explanation
CRF+BiLSTM The code is interpreted step by step

Explain

I've talked about it before forward_algorithm Is a function used to solve the sum of all path scores , The following will use a specific example to explain the flow of this function implementation .

First initialize a random emission matrix e_score (batch_size, seq_len, tags_size)

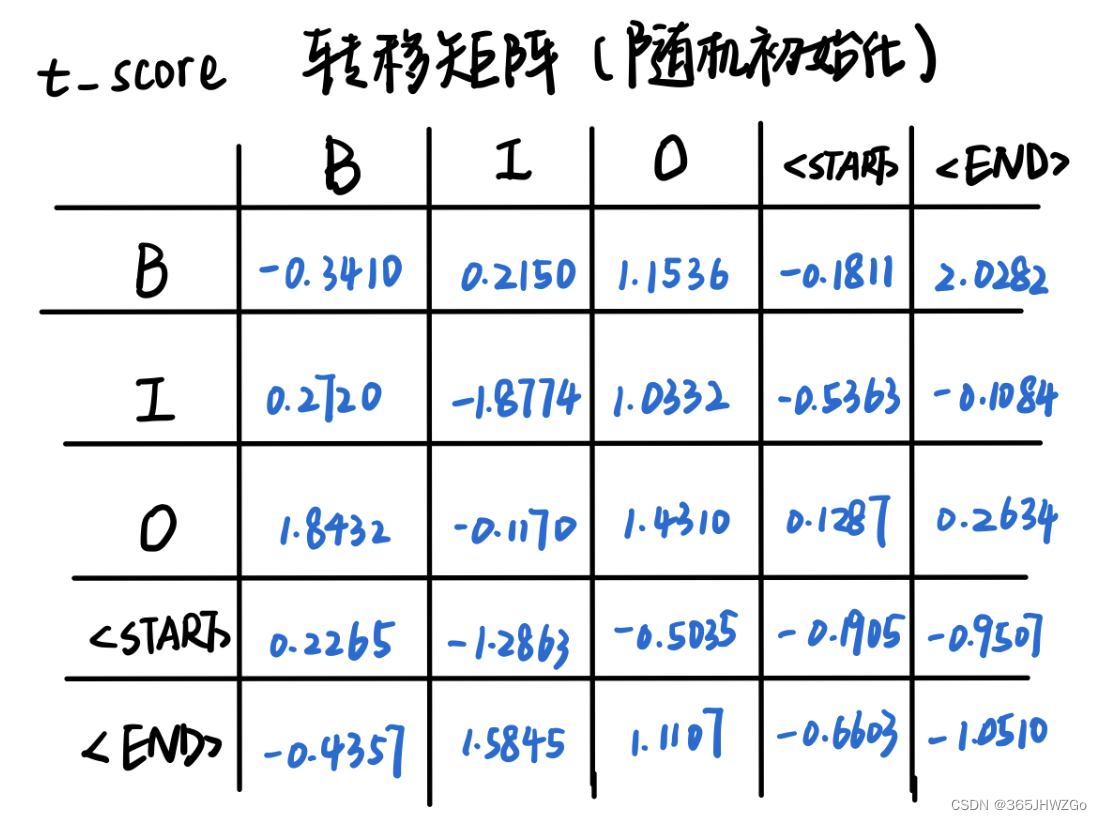
And then randomly initialize an emission matrix t_score (tags_size, tags_size)

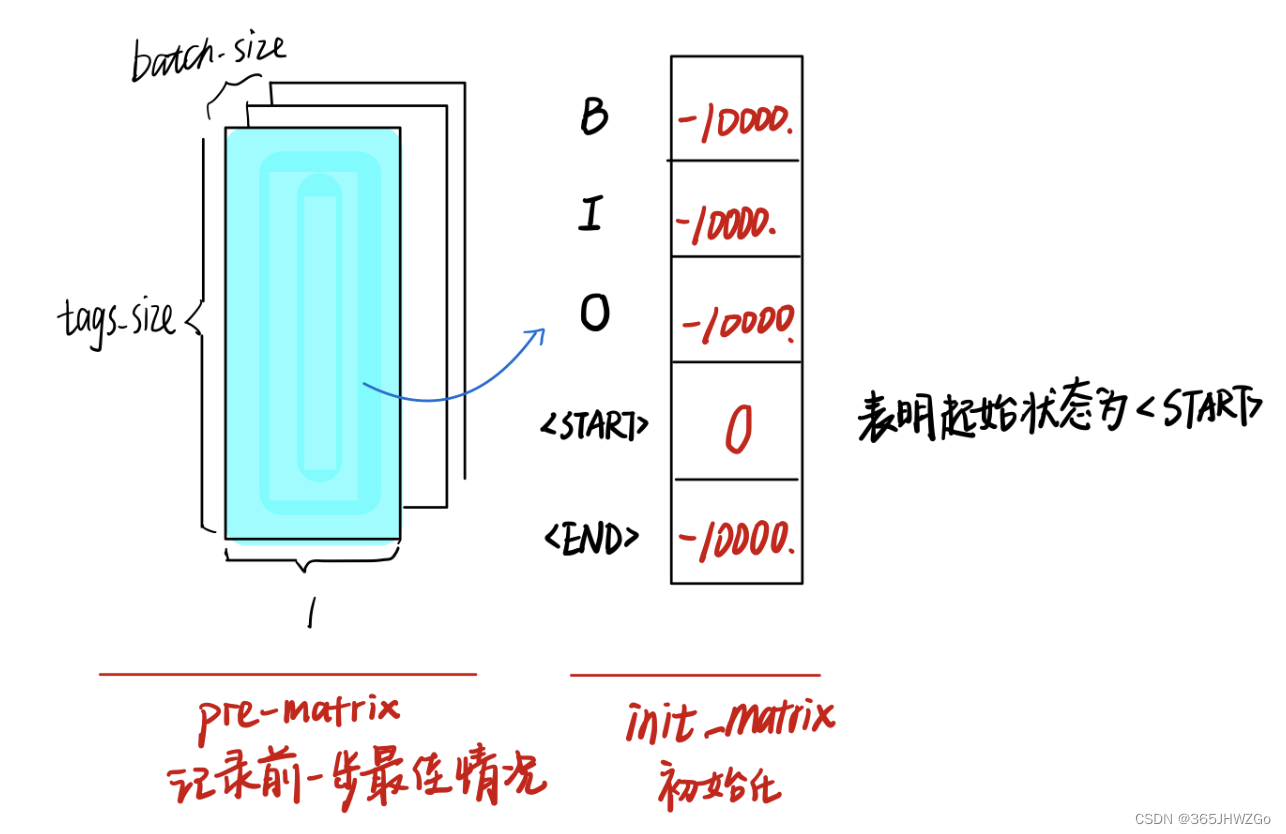
Create a init_matrix, Then make another copy for pre_matrix, Here, the model is erected for convenience of understanding (batch_size, 1, tags_size)

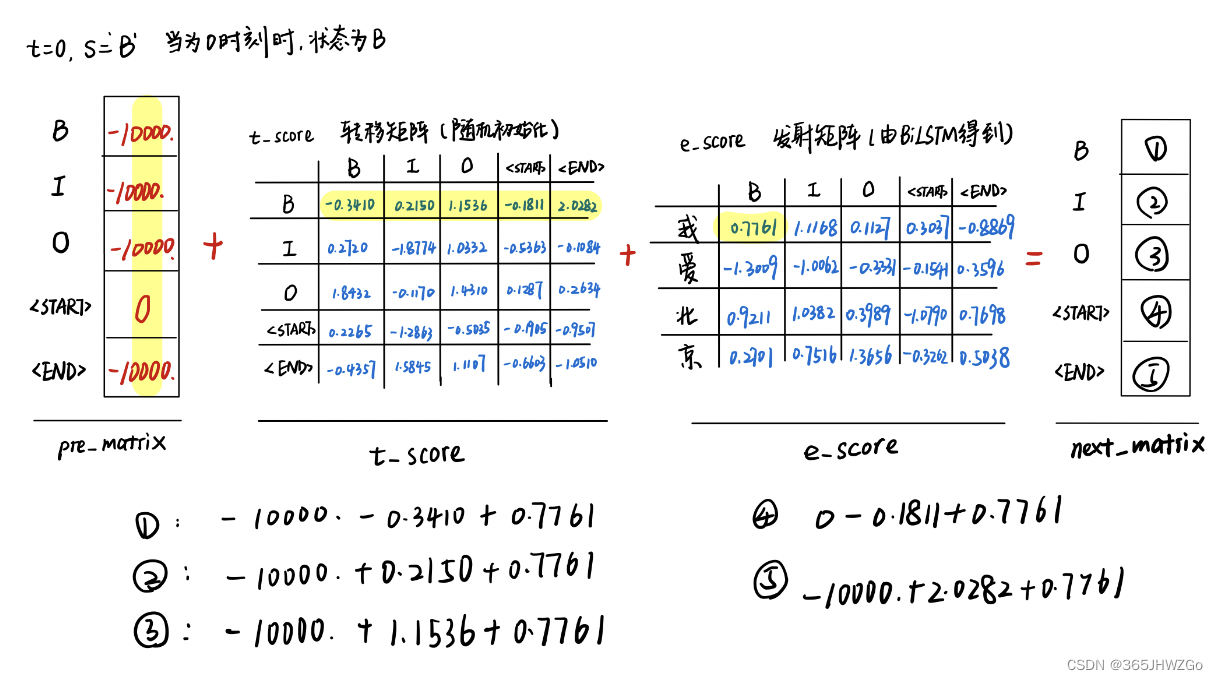
Here is only a demonstration of what was then engraved as 0, Status as ’B’ The calculation process of

It's all down here log_sum_exp Temporary variables in

Code

def forward_algorithm(self, e_matrix):

  # matrix  Is the sum of the total paths in the current state 
  init_matrix = torch.full((BATCH_SIZE, 1, tags_size), -10000.0)
  init_matrix[:, 0, self.s2i[START_TAG]] = 0.

  #  The optimal value of the previous step 
  pre_matrix = init_matrix

  #  Cycle time 
  for i in range(SEQ_LEN):
    #  Save the path value of the current time step 
    matrix_value = []
    #  Cycle state 
    for s in range(tags_size):
      #  Calculate the emission fraction , (BATCH_SIZE, 1, tags_size)
      e_score = e_matrix[:, i, s].view(BATCH_SIZE, 1, -1).expand(BATCH_SIZE, 1, tags_size)
      #  Calculate transfer score  (1,tags_size)
      t_score = self.t_score[s, :].view(1, -1)
      #  The next score  (BATCH_SIZE, 1, tags_size)
      next_matrix = pre_matrix + e_score + t_score
      # self.log_sum_exp(next_matrix) (BATCH_SIZE, 1)
      matrix_value.append(self.log_sum_exp(next_matrix))
      #  Record it in pre_matrix variable 
  	pre_matrix = torch.cat(matrix_value, dim=-1).view(BATCH_SIZE, 1, -1)

  #  The final variable ： Previous scores + The score transferred to the destination  (BATCH_SIZE, 1, tags_size)
  terminal_var = pre_matrix + self.t_score[self.s2i[STOP_TAG], :]
  alpha = self.log_sum_exp(terminal_var)
  # (BATCH_SIZE,1)
  return alpha

You can see here that it is not clear why you can get the sum of all paths by doing this , Actually , This is simply to simplify the calculation , But the disadvantage of this calculation is that it has been used many times logsumexp, This is actually a little different from the original value .

Ideal value
$$scor{e}_{ideal}=log(e^{S_1}+e^{S_2}+...+e^{S_N})\text{\hspace{1em}(1)}$$
Realistic value

$$\begin{array}{rl}scor{e}_{reality}& =log(\sum e^{pre+t})\\ & =log(\sum e^{log(\sum e^{pre+t+es})+t})\\ & =...\end{array}\text{\hspace{1em}(2)}$$
t->t_score
es->e_score
pre->pre_matrix

As shown in the figure above ,* The ball has been calculated from <START> To " I ", All statuses in the previous step are up to B Total path score of S1, seek logsumexp(S1) It was recorded that * Bulbar , Similarly, the sphere is where all the paths of the first two steps arrive " Love ", And all States are transferred to B Total path score of S2, seek logsumexp(S2) Record to the ball .

thus , Did you stop learning ？