当前位置:网站首页>MCS: continuous random variable - student's t distribution
MCS: continuous random variable - student's t distribution
2022-06-23 05:22:00 【Fight the tiger tonight】
Student’s t
Student’s t Distribution is also a very important distribution in statistical analysis , It is often used to test the significance of the mean value of variables .Student’s t Distribution is also called t Distribution , Similar to the standard normal distribution , But the tail can extend to the left and right , Depends on the parameters k k k freedom .
t Expectation and variance of distribution :
E ( t ) = 0 E(t) = 0 E(t)=0
V ( t ) = k k − 2 , k > 2 V(t) = \frac{k}{k - 2},k > 2 V(t)=k−2k,k>2
t Distribution properties :
- When k > 30 k > 30 k>30 when ,t The distribution approximates the standard normal distribution .
- t、chi-Square And the standard normal distribution :
t = z X 2 / k t = \frac{z}{\sqrt{\mathcal X^2 / k}} t=X2/kz
Generative obedience t Random variable of distribution
- Generate a standard normal variable : z ∼ N ( 0 , 1 ) z \sim N(0, 1) z∼N(0,1)
- Generate a degree of freedom k Of Chi-Square Variable : X k 2 \mathcal X_k^2 Xk2
- t = z / X k 2 / k t = z / \sqrt{\mathcal X_k^2 / k} t=z/Xk2/k
- Return t.
example : Generate a degree of freedom 6 Of t Variable :
- z = 0.71 z = 0.71 z=0.71
- X 6 2 = 6.29 \mathcal X_6^2 = 6.29 X62=6.29
- t = 0.71 / 6.29 / 6 = 0.693 t = 0.71 / \sqrt{6.29/6} = 0.693 t=0.71/6.29/6=0.693
- t = 0.693 t = 0.693 t=0.693
import numpy as np
import matplotlib.pyplot as plt
def generate_t_var(k=1):
z = np.random.normal(0, 1)
if k < 30:
c = (np.random.normal(0, 1, size=(k))**2).sum()
t = z / np.sqrt(c / k)
else:
z_ = np.random.normal(0, 1)
c = int(k + z_ * np.sqrt(2*k) + 0.5)
t = z / np.sqrt(c / k)
return t
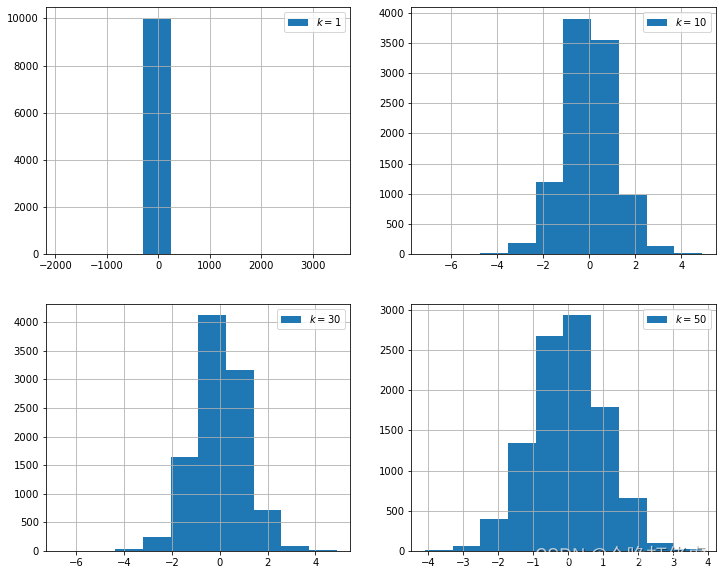
k = 1 、 10 、 30 、 50 k = 1、10、30、50 k=1、10、30、50
边栏推荐
- 618 how to break through the siege? Haier Zhijia: do a good job in digitalization of users
- VMware network connection error unit network service not found
- Investment risk management
- 应用挂了~
- pkav简单爆破
- MCS:连续随机变量——Chi-Square分布
- 【opencv450】 图像相减、二值化、阈值分割
- 大环境不好难找工作?三面阿里,幸好做足了准备,已拿offer
- 第九章 APP项目测试(1)
- 气象绘图软件Panoply使用教程 (不定时更新)
猜你喜欢
随机推荐
618 how to break through the siege? Haier Zhijia: do a good job in digitalization of users
Go 分组 & 排序
gis利器之Gdal(三)gdb数据读取
导出带水印的PDF
小时候 觉得爸爸就是天 无所不能~
Three methods of GNSS velocity calculation
Introduction and use of precise ephemeris
JDBC入门学习(三)之事务回滚功能的实现
HCIP 重发布实验
BGP second test
Calculate Euclidean distance and cosine similarity
APP自动化测试-Appium进阶
Strong push, quick start to software testing
Jenkins安装部署以及自动构建和发布jar应用
渗透测试基础 | 附带测试点、测试场景
MCS:离散随机变量——Uniform分布
A compiler related bug in rtklib2.4.3 B34
牛B程序员在“创建索引”时都会注意啥?
Memory model of JVM principle
小时候 觉得爸爸就是天 无所不能~









