论文笔记: 多标签学习 MSWL

摘要: 分享对论文的理解. 原文见 Zhang, J., Li, S., Jiang, M., & Tan, K. C. (2020). Learning from weakly labeled data based on manifold regularized sparse model. IEEE Transactions on Cybernetics, (pp. 1–14).

1. 论文贡献

• 解决半监督的带缺失值多标签学习问题. 其实有缺失标签的时候, 已经是半监督了. 这篇论文强调的是, 有些样本一个标签都不给.
• 全局与局部标签相关性.
• 稀疏性学习模型, 条件属性的辨别性.

2. 基本符号

符号	含义	说明
$\mathbf{X}\in {\mathbb{R}}^{n\times d}$	属性矩阵
$\mathbf{Y}\in \{-1,1{\}}^{n\times q}$	标签矩阵
$\mathbf{C}\in \{0,1{\}}^{n\times q}$	观测标签矩阵	$c_{ij}=0$ 对应于 $y_{ij}=-1$ 或 $1$
$\mathbf{\Omega }=\{1,\dots ,n\}\times \{1,\dots ,c\}$	观测标签位置集合
$\mathbf{W}\in {\mathbb{R}}^{m\times l}$	系数矩阵	仍然是线性模型
${\mathbf{w}}_i\in {\mathbb{R}}^m$	某一标签的系数向量
$\mathbf{C}\in {\mathbb{R}}^{l\times l}$	标签相关性矩阵	成对相关性, 不满足对称性

3. 算法

图 1. 算法总览

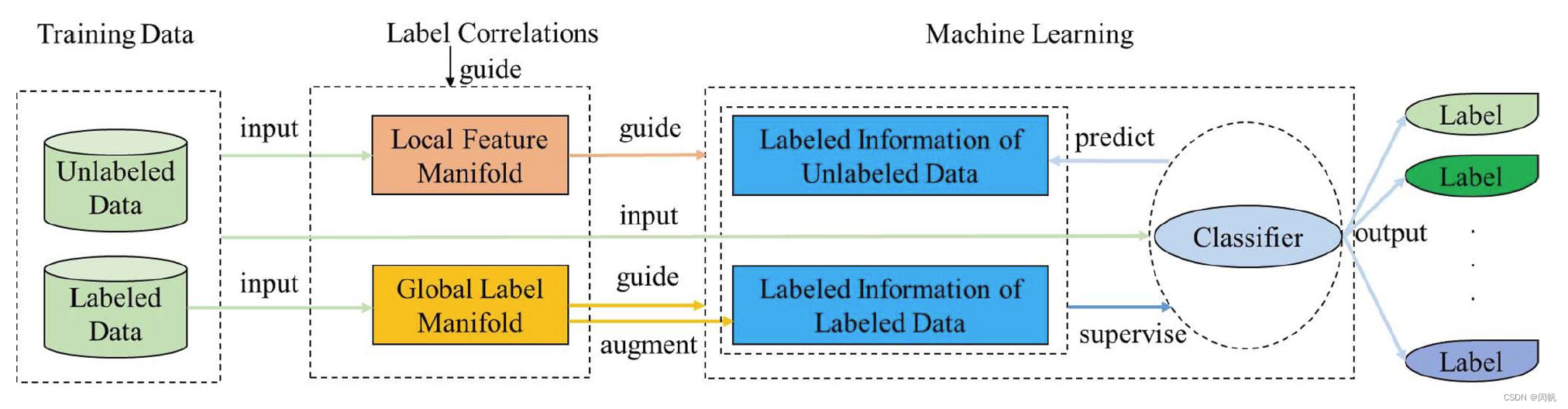
基本的优化目标:
$$\underset{\mathbf{W}}{\min }V(\mathbf{X},\mathbf{C},\mathbf{W})+\gamma \Omega (\mathbf{W})+\mu Z(\mathbf{X},\mathbf{C},\mathbf{W}),\text{\hspace{1em}(1)}$$
其中 $V$ 是损失函数, $Z$ 根据标签相关性信息增强弱标签学习能力.

3.1 损失函数

$$V(\mathbf{X},\mathbf{C},\mathbf{W})=\Vert \mathbf{X}\mathbf{W}-\tilde{\mathbf{Y}}{\Vert }_2^2,\text{\hspace{1em}(2)}$$
其中 $\tilde{\mathbf{Y}}$ 是从 $\mathbf{C}$ 计算而来, 希望拟合 $\mathbf{Y}$. 具体方法如下:
如果 $c_{ij}=0$, 表示缺值或负标签, 则
$${\tilde{c}}_{ij}=\sum _{p\in {\mathcal{N}}_j}{c}_{ip}{b}_{pj},\text{\hspace{1em}(3)}$$
其中 ${\mathcal{N}}_j$ 表示标签 $j$ 的所有邻居标签, $b_{pj}$ 表示标签 $p$ 与标签 $j$ 的相关性. 可以记为 (这里有点小的问题, 丢失了邻居信息)
$$\tilde{\mathbf{C}}=\mathbf{C}(\mathbf{B}+\mathbf{I}).$$
$${\tilde{y}}_{ij}=\{\begin{array}{ll}1,& {\tilde{c}}_{ij}\ge 1;\\ {\tilde{c}}_{ij},& 0<{\tilde{c}}_{ij}<1;\\ 0,& {\tilde{c}}_{ij}\le 0.\end{array}\text{\hspace{1em}(4)}$$

3.2 正则项

使用 $l_{2,1}$ 范数控制稀疏性.
$$\Omega (\mathbf{W})=\Vert \mathbf{W}{\Vert }_{2,1}=\sum _{i=1}^n\sqrt{\sum _{j=1}^t{w}_{ij}^2},$$
即逐行取 2 范数再相加. 更多理解见 这里.

3.3 标签相关性学习 (全局与局部的流形正则)

• 全局相关性
  $$\underset{{\mathbf{b}}_i}{\min }\Vert {\mathbf{C}}_{-i}{\mathbf{b}}_i-{\mathbf{c}}_i{\Vert }_2^2+\lambda \Vert {\mathbf{b}}_i\Vert ,\text{\hspace{1em}(6)}$$
  其中 ${\mathbf{C}}_{-i}$ 是将第 $i$ 列标签全部置为 0 所获得的不完整矩阵. 该式的具体优化方法略, 反正我也没看懂.
• 局部相关性
  $$\underset{\mathbf{S}}{\min }\sum _{i=1}^n\Vert {\mathbf{x}}_i-\sum _{j\in {\mathcal{N}}_i}{s}_{ji}{\mathbf{x}}_j{\Vert }^2,\text{\hspace{1em}(11)}$$
  其中 $K$ 是邻居数量, $s_{ij}$ 是 ${\mathbf{x}}_i$ 与其邻居 ${\mathbf{x}}_j$ 的相似性.

注意原文有几个小问题:

• $s_{ij}\in \mathbf{S}$ 的写法不正确, 后者并非一个矩阵. 其实不写也没有歧义;
• 第 $j$ 个邻居与第 $j$ 个标签之间, 相关了一个间址, 因此使用 $j\in {\mathcal{N}}_i$;
• 怀疑下标 2 没写, 导致不是 2 范数.

最后
$$Z(\mathbf{X},\mathbf{C},\mathbf{W})=\alpha \Vert \mathbf{W}-\mathbf{W}\mathbf{B}{\Vert }_F^2+\beta \Vert \mathbf{X}\mathbf{W}-\mathbf{S}\mathbf{X}\mathbf{W}{\Vert }_F^2$$

3.4 扩展到半监督学习

自悟.

4. 小结

• 三个部分各司其职.
• 流行学习.