Reference resources :https://www.zhihu.com/question/40049682/answer/1420483558
There are two situations :
One 、 That's ok X Column
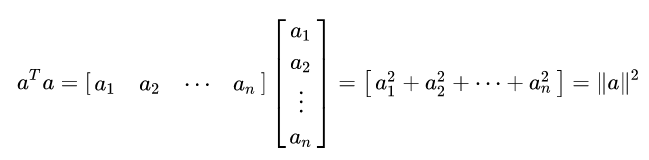
Is the square of its length .
Two 、 Column X That's ok

It is usually dealt with ( normalization ):

For any vector b , It projects to a The vector on must be :

--------------------------------------------------------------------------------------------------------------------------------
About columns X That's ok Proof of projection of :

There are two vectors ![[ The formula ]](/img/e1/369a781c16867fbc3e4714e3f8632a)
![[ The formula ]](/img/73/ea7d60226debb115e4febcabd9cc08)
![[ The formula ]](/img/3a/aa6c2a7d5845d97acbb4d407bb391c)
![[ The formula ]](/img/fe/8c647d303a3ef816c87e16d5a37a59)
This process is obviously a linear transformation , So let's record this linear transformation as : ![[ The formula ]](/img/33/00447bdb3f09d34f9863bd04eab508)
So according to its definition, there are :
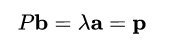
here ![[ The formula ]](/img/8c/3f988bed4e3828caf6e0da35d61dc2)
![[ The formula ]](/img/82/044817b60f52f0efc17faa65ea0576)
![[ The formula ]](/img/3a/aa6c2a7d5845d97acbb4d407bb391c)
Consider from the triangle rule
vector ![[ The formula ]](/img/45/c9b597a76d871c51d54f11317522fe)
![[ The formula ]](/img/73/ea7d60226debb115e4febcabd9cc08%2C%5Cmathbf%7Bp%7D)
It is not difficult to see from the geometric relationship ![[ The formula ]](/img/3a/aa6c2a7d5845d97acbb4d407bb391c+%5Cbot%5Cmathbf%7Be%7D+)
Then it will be transformed into a quantitative relationship
It is not difficult to draw a conclusion from the equivalence relation of the marked red :
Note that the default vectors are column vectors , So scalars can be written directly as :
At this point, let's turn back to linear transformation
That's what's mentioned above Projection matrix The whole process of proof .
![[ The formula ]](/img/3f/4aa6632169487211398ec6d7a6a656)
![[ The formula ]](/img/e3/22ab6dba0ebc8d0451ef9b8b478a33)
![[ The formula ]](/img/02/b665fc8a16e06ee6e6066909348c56)
![[ The formula ]](/img/33/00447bdb3f09d34f9863bd04eab508%5Cmathbf%7Bb%7D%3D%5Cmathbf%7Ba%7D%5Clambda%3D%5Cmathbf%7Ba%7D%5Cfrac%7B%5Cmathbf%7Ba%7D%5E%7BT%7D+%5Cmathbf%7Bb%7D%7D%7B%5Cmathbf%7Ba%7D%5E%7BT%7D+%5Cmathbf%7Ba%7D%7D++%3D%5Cfrac%7B%5Ccolor%7BRed%7D%7B+%5Cmathbf%7Ba%7D%5Cmathbf%7Ba%7D%5E%7BT%7D%7D++%7D%7B%5Cmathbf%7Ba%7D%5E%7BT%7D+%5Cmathbf%7Ba%7D%7D%5Cmathbf%7Bb%7D+)


![[WPF] XAML code skills that can be directly used for converting CAD engineering drawings to WPF](/img/a1/09d2dc0ec47c54530da4d42d218d1c.jpg)




![[invitation letter] on March 4, the platform enabled digital intelligence Innovation -- UFIDA BiP PAAS cloud platform IUAP digital intelligence hundred cities forum · Jinan Station](/img/99/802b45296a96e866e9d16fa7017d31)
