当前位置:网站首页>[note] linear regression
[note] linear regression
2022-07-23 16:35:00 【Sprite.Nym】
List of articles
One 、 summary
1.1 Linear regression
Regression is a widely used prediction modeling technology , This kind of technology The core is that the predicted result is a continuous variable .
Decision tree , Random forests , The prediction label of classification algorithms such as support vector machine classifier is the classification variable , More than {0,1} To express , Unsupervised learning algorithms, such as PCA,KMeans Does not solve the label , Pay attention to the difference .
Regression algorithm comes from statistical theory , It may be one of the earliest machine learning algorithms , It is widely used in reality , Including the use of other Economic indicators predict the stock market index , According to the characteristics of jet flow Predict the precipitation in the region , According to the company's advertising expenses Forecast total sales , Or according to the residual carbon in organic matter -14 To estimate the age of fossils and so on , as long as All features based prediction of continuous variable demand , We all use regression techniques .
Since linear regression is derived from statistical analysis , It is an important algorithm combining machine learning and statistics . Generally speaking , We believe that statistics focuses on a priori , And machine learning values results , Therefore, in machine learning, collinearity and other factors that may affect the model will not be excluded for linear regression in advance , Instead, the model will be built first to see the effect . After the model is established , If the effect is not good , We will rule out the factors that may affect the model according to the guidance of Statistics . Our course will explain regression algorithms from the perspective of machine learning , If you want to understand statistics , Various statistics textbooks can meet your needs .
The mathematics of regression algorithm is relatively simple . Usually , There are two ways to understand linear regression : The angle of matrix and the angle of Algebra . Almost all machine learning textbooks understand linear regression from the perspective of Algebra . Relative , There has been a lack of systematic use of matrices to interpret algorithms in our courses , So in this class , I will use the matrix method all the way ( The way of Linear Algebra ) Show you the face of returning to the big family .
After this class , You need to have a relatively comprehensive understanding of linear models , In particular, we need to master what advantages and problems exist in the linear model , And how to solve these problems .
1.2 SKlearn Linear regression in
sklearn The linear model module in is linear_model, We once mentioned this module when learning logical regression .linear_model Contains a variety of classes and functions , The classes and functions related to logistic regression are not listed here .
| – | – |
|---|---|
| Ordinary linear regression | |
| linear_model.LinearRegression | Linear regression using ordinary least squares |
| Ridge return | |
| linear_model.Ridge | Ridge return , One will L2 Linear least squares regression as a regularization tool |
| linear_model.RidgeCV | Ridge regression with cross validation |
| linear_model.RidgeClassifier | Classifier of ridge regression |
| linear_model.RidgeClassifierCV | Classifier of ridge regression with cross validation |
| linear_model.ridge_regression | 【 function 】 Use normal equation method to solve ridge regression |
| LASSO | |
| linear_model.Lasso | Use L1 A linear regression model trained as a canonical tool |
| linear_model.LassoCV | With cross validation and regularization iteration path Lasso |
| linear_model.LassoLars | Using the minimum angle regression solution Lasso |
| linear_model.LassoLarsCV | With cross validation, it is solved by minimum angle regression Lasso |
| linear_model.LassoLarslC | Use BIC or AIC Model selection , Using the minimum angle regression solution Lasso |
| linear_model.MultiTaskLasso | Use L1/L2 Mixed norm as a regularization tool for training multiple labels Lasso |
| linear_model.MultiTaskLassoCV | Use L1/L2 The mixed norm is trained as a regularization tool , Multiple tags with cross validation Lasso |
Two 、 Multiple linear regression
2.1 The basic principle of multiple linear regression
Linear regression is the simplest regression algorithm in machine learning , Multiple linear regression refers to a linear regression problem in which a sample has multiple characteristics . For one there is n n n Sample of the features i i i for , Its regression results can be written into a familiar equation :
y ^ = ω 0 + ω 1 x i 1 + ω 2 x i 2 + . . . + ω n x i n \hat y= \omega_0 +\omega_1x_{i1}+\omega_2x_{i2}+...+\omega_nx_{in} y^=ω0+ω1xi1+ω2xi2+...+ωnxin
Here's the formula ω \omega ω It's the parameters of the model , ω 0 \omega_0 ω0 Is the intercept term , ω 1 \omega_1 ω1~ ω n \omega_n ωn It's called the regression coefficient . Sometimes used β \beta β perhaps θ \theta θ Express . This formula is similar to our y = a x + b y= ax+b y=ax+b The same nature . y y y Is our target variable , Also known as , label . x i 1 x_{i1} xi1~ x i n x_{in} xin Is the sample i i i On the characteristics of . Consider that we have m m m Samples , Then our regression equation can be written as :
y ^ = ω 0 + ω 1 x 1 + ω 2 x 2 + . . . + ω n x n \hat y= \omega_0 +\omega_1x_{1}+\omega_2x_{2}+...+\omega_nx_{n} y^=ω0+ω1x1+ω2x2+...+ωnxn
among y ^ \hat y y^ It includes m Column vector of regression results of all samples . Vectors are in bold . The above equation can be written in the following matrix form :

Simplified version : y ^ = X ω \hat y=X\omega y^=Xω
The task of linear regression , Is to construct a prediction function to map the input characteristic matrix X And tag values g The linear relationship of , This prediction function is written differently in different textbooks : f ( x ) f(x) f(x) or h ( x ) h(x) h(x) It's possible . But anyway , The essence of this prediction function is the model we need to build , The core of constructing prediction function is to find out the parameter vector of the model . But how can we solve the parameter vector ?
2.2 Loss function
When we learn machine learning , We said we use training sets to train models , Modeling is to pursue the best performance of the model in the test set , Therefore, the evaluation index of the model is often used to measure the performance of the model on the test set . In linear regression , It is necessary to solve parameters based on training data , And hope that the trained model can fit the training data as much as possible , That is, the prediction accuracy of the model on the training set is closer to 100% The better .
therefore , We use **" Loss function " This evaluation index , Come on The measurement parameter is w The size of information loss caused by the model fitting training set , And measure the parameters w The advantages and disadvantages of **. If you model with a set of parameters , The model performs well on the training set , Then we say that the loss in the process of model fitting is very small , The value of the loss function is very small , This set of parameters is excellent ; contrary , If the model performs badly on the training set , The loss function will be very large , The model is not trained enough , Poor results , This set of parameters is relatively poor .
So we hope to solve the parameters u when , The loss function is the smallest . In this way, the fitting effect of the model on the training data will be the best . The accuracy will be as high as possible . So the way we solve the parameters , Is the process of optimizing the loss function .
Be careful : Some models do not need to solve parameters , There is no loss function , such as KNN, Decision tree . Loss function of linear regression :
Loss function of linear regression :
∑ i = 1 m ( y i − y ^ i ) 2 = ∑ i = 1 m ( y i − X i ω ) 2 \displaystyle\sum_{i=1}^{m}(y_i-\hat y_i)^2=\displaystyle\sum_{i=1}^{m}(y_i-X_i\omega)^2 i=1∑m(yi−y^i)2=i=1∑m(yi−Xiω)2
y i y_i yi Is the sample i i i The corresponding real label , y ^ i \hat y_i y^i Is the sample i i i In a certain set of parameters ω \omega ω Forecast tab under .
First , This loss function represents the vector y i − y ^ i y_i-\hat y_i yi−y^i Of L2 The square result of the normal form ,L2 The essence of paradigm is European distance , That is, each point on the two vectors corresponds to the peace and square again after meeting , Here we only do the sum of squares , No more prescriptions .
therefore , We get the loss function :L2 normal form , Sum of squares of Euclidean distances .
Under this square result , our g and g They are our real labels and predicted values , in other words , This loss function actually calculates the distance between our real label and the predicted value . therefore , We believe that this loss function measures the difference between the prediction results of our model and the real label , Therefore, we certainly hope that the smaller the difference between our prediction results and the real value, the better . So our goal can be transformed into :
min ω ∣ ∣ y − X ω ∣ ∣ 2 2 \displaystyle \min_{\omega}{||y-X\omega||_2}^2 ωmin∣∣y−Xω∣∣22
2.3 Least square method
Now the problem turns into solving let RSS Minimized parameter vector ω \omega ω, By minimizing the difference between the real value and the predicted value RSS The method to solve the parameters is called the least square method . The first step in solving the extreme value is often to solve the first derivative and make the first derivative equal to 0, The least square method is not immune to vulgarity . therefore , We now sum of squares of residuals RSS On the parameter vector ω \omega ω Derivation .
Derivation process .
2.4 linear_model.LinearRegression
class sklearn.linear_mode1.LinearRegression(fit_intercept=True, normalize=False, copy_x=True, n_jobs=None)
| Parameters | meaning |
|---|---|
| fit_intercept | Boolean value , Not required , The default is True. Whether to calculate the intercept of this model . If set to False, Intercept... Is not calculated . |
| normalize | Boolean value , Not required , The default is False, When fit_intercept Set to False when , This parameter will be ignored . If True, Then the characteristic matrix X The mean value will be subtracted before entering the regression ( Centralization ) And divide by L2 normal form ( The zoom ). If you want to standardize , Please be there. fit Data before use preprocessing Standardized special classes in modules StandardScaler. |
| copy_x | Boolean value , Not required , The default is True If it is true , Will be in X.copy() Operation on top , Otherwise, the original characteristic matrix X May be affected by linear regression and cover integers or None, Not required , The default is None. Number of jobs used for calculation . Only in the return of multiple labels . |
| n_jobs | And when the data volume is large enough . Unless None stay joblib.parallel_backend In the context of , otherwise None Unity is expressed as 1. If input -1, It means to use all CPU To calculate . |
The class of linear regression is probably the simplest class we have learned so far , Only four parameters can complete a complete algorithm . And you can see , None of the these parameters is required , There are no irreplaceable parameters for our model . This explanation , Performance of linear regression , It often depends on the data itself , Not our ability to tune parameters , Therefore, linear regression has high requirements for data . Fortunately, , In reality, most continuous variables , You can see more or less velvet connections . So linear regression is simple , But it's powerful .
By the way ,sklearn Linear regression in can deal with multi label problems , Only need fit You can enter a multi-dimensional label when .
边栏推荐
- 华为新版Datacom认证介绍
- [2023 approved in advance] BOE
- C#中单例模式的实现
- Middle aged crisis, retired at the age of 35, what do migrant workers take to compete with capitalists?
- Memory methods of big end mode and small end mode
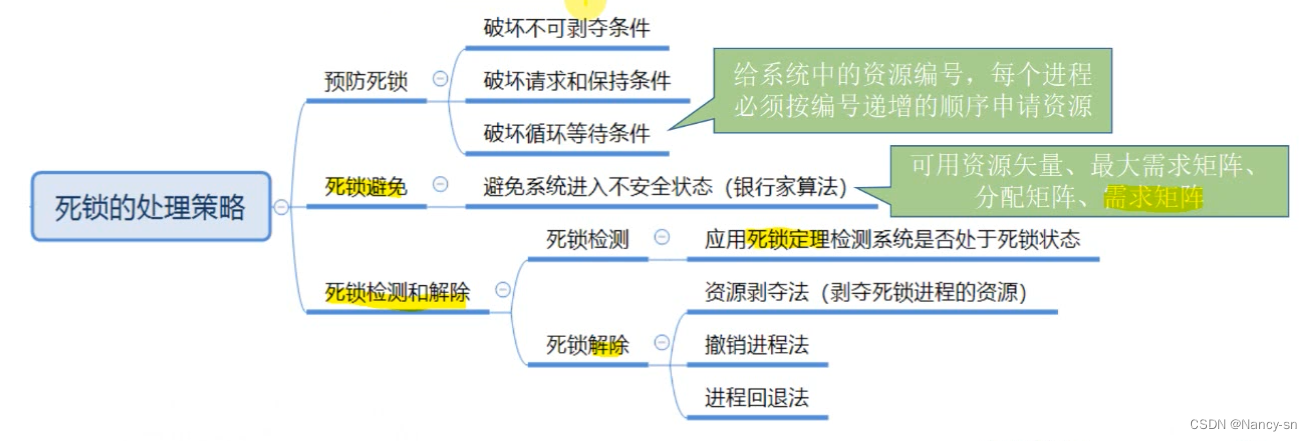
- Three handling strategies of deadlock
- [suctf 2018]multisql (MySQL precompiled)
- fastadmin,非超级管理员,已赋予批量更新权限,仍显示无权限
- 移动端H5 - 手撸一个生命线 timeline
- 机器狗背冲锋枪射击视频火了,网友瑟瑟发抖:stooooooooppppp!
猜你喜欢

動態規劃背包問題之完全背包詳解

Basic concept and deployment of kubernetes
Three handling strategies of deadlock

table自定义表格的封装

Esp8266 nodemcu flash file system (spiffs)
SOC的第一个Hello_World实验
![[2022 freshmen learning] key points of the second week](/img/5f/87a30e898b4450af5f2eb0cf77e035.png)
[2022 freshmen learning] key points of the second week

ICML 2022 | sparse double decline: can network pruning also aggravate model overfitting?

动态规划背包问题之01背包详解

竞赛大佬在华为:网络专家出身斯坦福物理系,还有人“工作跟读博差不多”...
随机推荐
MySQL中几种常见的 SQL 错误用法
激光共聚焦如何选择荧光染料
FPGA HLS multiplier (pipeline vs. ordinary simulation)
Cloudcompare & PCL normal vector space sampling (NSS)
pytest接口自动化测试框架 | pytest常用运行参数
数据库的备份和还原
vulnstack红日-4
16 automated test interview questions and answers
锁相环工作原理,比如我们8MHZ晶振如何让MCU工作在48MHZ或者72MHZ呢
智慧民航新业态崭露头角,图扑数字孪生入局民航飞联网
2022蓝帽杯初赛wp
EmguCV录制视频
【2022新生学习】第二周要点
Bean validation beginner ----02
The competition boss is in Huawei: network experts are from Stanford physics department, and some people "work as much as reading a doctoral degree"
nport串口服务器原理,MOXA串口服务器NPORT-5130详细配置
Convert.Calss file to.Jar idea
苹果x充电慢是什么原因_iPhone 12支持15W MagSafe无线充电,未来苹果手机的充电会发生什么?_充电器…
MySQL soul 16 ask, how many questions can you hold on to?
The protection circuit of IO port inside the single chip microcomputer and the electrical characteristics of IO port, and why is there a resistor in series between IO ports with different voltages?