当前位置:网站首页>Record the use process of fenics
Record the use process of fenics
2022-06-26 16:52:00 【White rice】
Occasionally I need to use fenics To calculate , But all kinds of unfamiliar , Every time I look online , There is a lot of information , and fenics The updated version , Many functions report errors , So here is a record of your own use process .
At the same time, it is necessary to refer to fenics Introduction to basic types in : Docs » User manual » Form language).
Catalog
- 1. After defining the grid and space , Get the number of degrees of freedom of the space 、 The value of the function at the degree of freedom 、
- 2. take == Two functions as components form a vector function ==
- 3. The resulting stiffness matrix is transformed into `numpy.array()` Format
- obtain Constant Value
- Remove from the solver "Solving linear variational problem" Tips
- Get the value of the interpolation function at a certain point
1. After defining the grid and space , Get the number of degrees of freedom of the space 、 The value of the function at the degree of freedom 、
from dolfin import *
import numpy as np
mesh = UnitSquareMesh(4, 4)
# Coordinate values at mesh nodes
mesh_coor = mesh.coordinates()
# Building scalar and vector spaces
space_S1 = FunctionSpace(mesh, 'CG', 1) # 1 Express Lagrange 1 Dimension
space_S3 = VectorFunctionSpace(mesh, 'CG', 1, dim=3)
# Get the number of degrees of freedom
dof_f1 = np.array(df.dof_to_vertex_map(space_S1), dtype=int)
dof_f3 = np.array(df.dof_to_vertex_map(space_S3), dtype=int)
# establish space_S1 Interpolation on f1, And get the value of the function at the degree of freedom
f1 = interpolate(df.Expression("1.0+0*x[1]", degree=1), space_S1)
val_dof_f1 = f1.vector().get_local()
# Calculate the function value at the mesh node
v_vertex = f1.compute_vertex_values(mesh)
# Take the component of the gradient
Df0 = grad(f1)[0]
Df1 = grad(f1)[1]
# # stay Docs » User manual » Form language Mid search grad You can see :
# # In UFL, the following pairs of declarations are equivalent:
# Dfi = grad(f)[i]
# Dfi = f.dx(i)
# Dvi = grad(v)[i, j]
# Dvi = v[i].dx(j)
# DAi = grad(A)[..., i]
# DAi = A.dx(i)
# # for a scalar expression f, a vector expression v, and a tensor expression A of arbitrary rank.
above And get the value of the function at the degree of freedom It should be noted that fenics It started with f1.vector().array(), But this latest version is no longer available ( See Replace vector().array() to vector().get_local()).
2. take Two functions as components form a vector function
from dolfin import *
mesh = UnitSquareMesh(4, 4)
V = FunctionSpace(mesh, 'CG', 1)
u = Function(V)
u.interpolate(Expression("1+0*x[0]", degree=1))
v = Function(V)
v.interpolate(Expression("2+0*x[0]", degree=1))
W = VectorFunctionSpace(mesh, 'CG', 1, dim=2)
w = Function(W)
ua = u.vector().get_local()
va = v.vector().get_local()
wa = w.vector().get_local()
wa[::2] = ua
wa[1::2] = va
w.vector().set_local(wa)
3. The resulting stiffness matrix is transformed into numpy.array() Format
a = inner(grad(u), grad(v)) * dx
aa = assemble(a)
aM = aa.array()
L = inner(f, q) * dx
ll = assemble(L)
l1[:] # This lists all the values of the right-hand end item
obtain Constant Value
aa = Constant(1e-3)
print(aa) # Coefficient(FunctionSpace(None, FiniteElement('Real', None, 0)), 49)
aa_ = float(aa)
print(aa_)
Remove from the solver “Solving linear variational problem” Tips
add to set_log_active(False) You can turn off all prompts ( Include ‘Error’, ‘Warning’ …)
Get the value of the interpolation function at a certain point
For example, it defines fenics Space Vh, And given True solution Phi = Expression("x[0] + x[1]", degree=3) ( namely Phi = x + y), then Phi Interpolate to Vh In the space : Phi_h = interpolate(Phi, Vh), We want to be spot P=(0.3, 1.2) The value of the function at
Phi_h = interpolate(Phi, Vh)
P = (0.3, 1.2)
val = Phi_h(P)
边栏推荐
- Scala 基礎 (二):變量和數據類型
- 无需人工先验!港大&同济&LunarAI&旷视提出基于语义分组的自监督视觉表征学习,显著提升目标检测、实例分割和语义分割任务!...
- 【从删库到跑路】JDBC 完结篇(一天学完系列!!学完赶紧跑!)
- Learn about common functional interfaces
- GUI+SQLServer考试系统
- day10每日3题(2):统计最大组的数目
- In a bad mood, I just write code like this
- 5g is not flat and 6G is restarted. China leads wireless communication. What is the biggest advantage of 6G?
- 构造函数和析构函数
- Redis 概述整理
猜你喜欢

无需人工先验!港大&同济&LunarAI&旷视提出基于语义分组的自监督视觉表征学习,显著提升目标检测、实例分割和语义分割任务!...
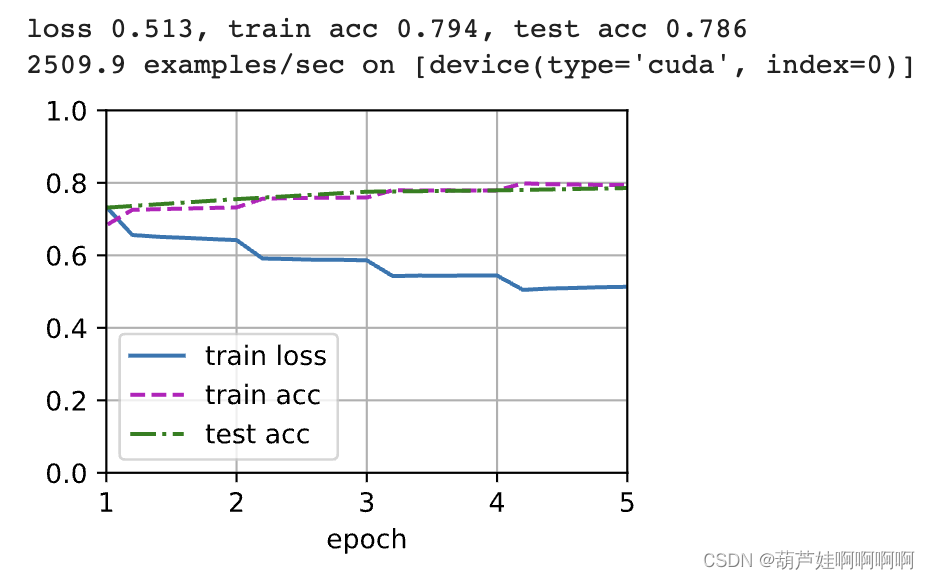
Natural language inference with attention and fine tuning Bert pytorch

Research on natural transition dubbing processing scheme based on MATLAB

GUI+SQLServer考试系统
Scala Foundation (2): variables et types de données

防火 疏散 自救…这场安全生产暨消防培训干货满满!

Sandboxed container: container or virtual machine

Science | 红树林中发现的巨型细菌挑战传统无核膜观念

当一个程序员一天被打扰 10 次,后果很惊人!
基于STM32+华为云IOT设计的云平台监控系统
随机推荐
The first open source MySQL HTAP database in China will be released soon, and the three highlights will be notified in advance
Niuke programming problem -- dynamic programming of must brush 101 (a thorough understanding of dynamic programming)
Interpretation of new plug-ins | how to enhance authentication capability with forward auth
Leetcode 1169. Query invalid transactions (if the amount of data is small, this problem still needs to be solved by violent enumeration)
【毕业季】致毕业生的一句话:天高任鸟飞,海阔凭鱼跃
对NFT市场前景的7个看法
[force deduction question] two point search: 4 Find the median of two positive arrays
[from database deletion to running] JDBC conclusion (finish the series in one day!! run as soon as you finish learning!)
Data analysis - numpy quick start
[understanding of opportunity -31]: Guiguzi - Daoyu [x ī] Crisis is the coexistence of danger and opportunity
Introduction to minimal API
Toupper function
Scala 基础 (二):变量和数据类型
板卡的分级调试经验
Least squares system identification class II: recursive least squares
NFT 交易市场社区所有化势不可挡
知道这几个命令让你掌握Shell自带工具
JS tutorial using electron JS build native desktop application ping pong game
Natural language inference with attention and fine tuning Bert pytorch
Scala Foundation (2): variables et types de données
