Advanced thinking on application scenarios of standardization, maximum normalization and mean normalization

This article belongs to the summary of knowledge points , The content belongs to excerpt and sorting

One 、 Basic concepts

 

 

 

---

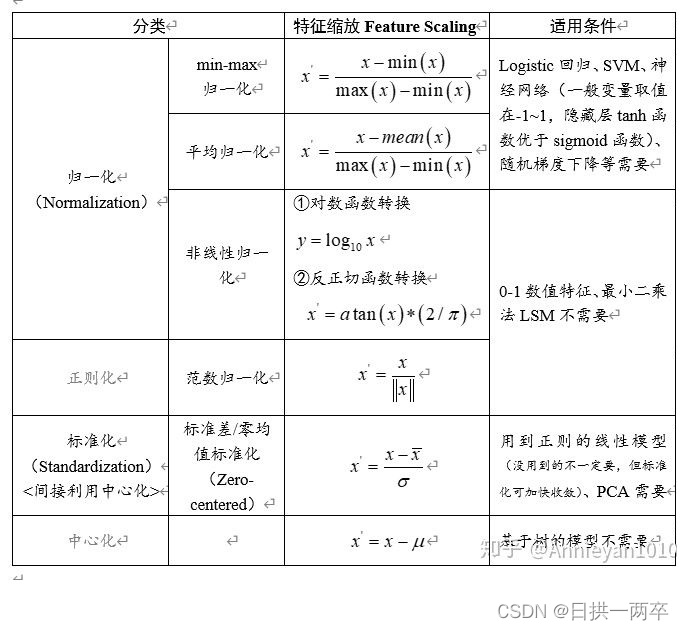
Two 、  Different normalization methods are described ：

2.1 Maximum normalization

The method of linearizing the original data is transformed into [0 1] The scope of the , This method realizes the equal scaling of the original data . By using the maximum and minimum values of variable values （ Or the maximum ） Convert raw data into data bounded by a specific range , So as to eliminate the influence of dimension and order of magnitude , Change the weight of variables in the analysis to solve the problem of different measures . Because the extremum method is only related to the two extreme values of the maximum and minimum of the variable in the process of dimensionless variable , It has nothing to do with other values , This makes the method rely too much on two extreme values when changing the weight of each variable .

2.2 Mean normalization

Mean normalization and maximum normalization are basically the same , Only the denominator is x-mean(x), The data will be compressed in [-1,1] The range of

2.3 Standardization method

That is, the value of each variable and its average value μ Divided by the standard deviation of the variable σ. Although this method makes use of all the data information in the dimensionless process , However, this method not only makes the mean values of the transformed variables the same after dimensionless , And the standard deviation is the same , That is, dimensionless, it also eliminates the difference in the degree of variation of each variable , Thus, the importance of the transformed variables in the cluster analysis is the same . And in the actual analysis , The importance of each variable in the analysis is often determined according to the difference of its value in different units , If the difference is large, the analysis weight is relatively large .

2.4 Nonlinear normalization

• Logarithmic function conversion ：y = log10(x)
• Inverse cotangent function conversion ：y = atan(x) * 2 / π
• It is often used in scenarios with large data differentiation , Some values are very large , Some are very small . Through some mathematical functions , Mapping the original values . The method includes log、 Index , Tangent, etc . According to the distribution of data , The curve that determines the nonlinear function , such as log(V, 2) still log(V, 10) etc. .

2.5  Centralization

The value of each variable and its mean μ The difference between the

2.6 Icon

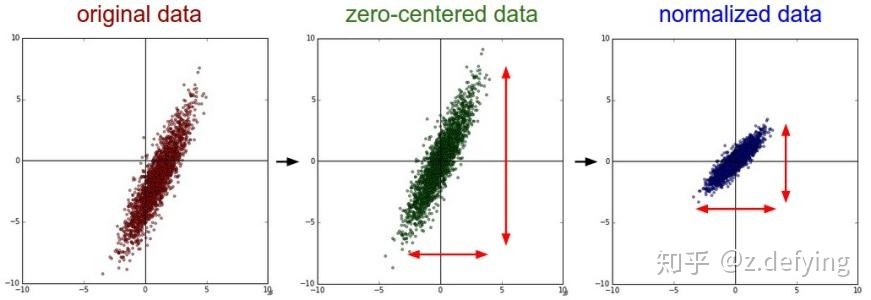
Raw data distribution 、 Zero mean data distribution 、 Normalized data distribution  

You can see mean Both normalization and standardization move the data distribution center to the origin , Normalization does not change the shape of the data distribution , Standardization makes the distribution of sample data approximate to a certain distribution .

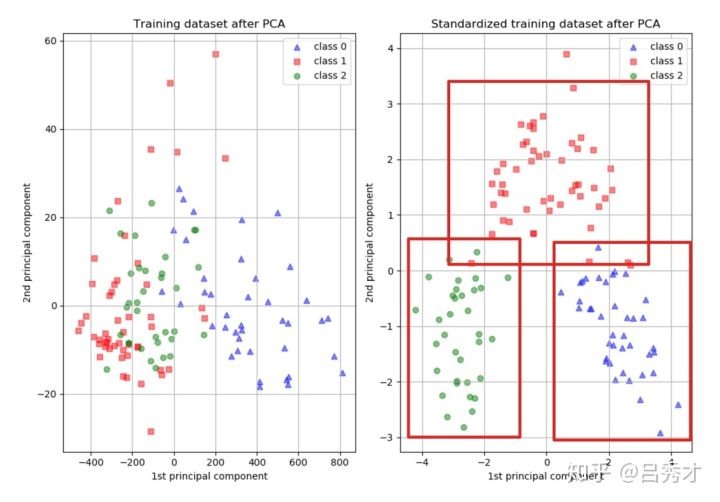
Standardization is good for PCA The impact of dimensionality reduction

---

3、 ... and 、 How to choose

The difference between normalization and Standardization ： Normalization is to convert the eigenvalues of samples to the same dimension and map the data to [0,1] perhaps [-1, 1] Within the interval , Only determined by the extreme value of the variable , Because the interval scaling method is a kind of normalization . Standardization deals with data according to the columns of characteristic matrix , It is through seeking. z-score Methods , Convert to standard normal distribution , Related to the overall sample distribution , Each sample point can have an impact on Standardization . What they have in common is that they can eliminate the errors caused by different dimensions ; It's all a linear transformation , It's all about vectors X Compress to scale and then translate .

The difference between standardization and centralization ： Standardization is the original score minus the mean and then divided by the standard deviation , Centralization is the original score minus the average . Therefore, the general process is to centralize first and then standardize .

When to use normalization ？ When to use standardization ？

1. If there is a requirement for the output range , Use normalization .
2. If the data is stable , There is no extreme maximum or minimum , Use normalization .
3. If the data has outliers and more noise , Use standardization , The influence of outliers and extremes can be avoided indirectly through centralization .

Generally speaking , It is recommended to give priority to the use of standardization .

3.1 Which models must be normalized / Standardization

3.1.1 SVM

Different models have different assumptions about the distribution of features . such as SVM With Gaussian kernels , All dimensions share one variance , This assumes that the characteristic distribution is circular , If you input an ellipse, it's a hole , So simple normalization is not good enough .

3.1.2 KNN、PCA、Kmeans

Models that need to measure distance , Generally, when the eigenvalue difference is large , Will be normalized / Standardization . Otherwise it will appear “ Large numbers take decimals ”.

In the classification 、 Clustering algorithm , When distance is needed to measure similarity 、 Or use PCA Technology for dimensionality reduction , Standardization performs better . When it comes to distance measurement 、 Covariance calculation 、 When the data does not conform to the positive distribution , The normalization method can be used . For example, in image processing , take RGB After the image is converted to a grayscale image, its value is limited to [0 255] The scope of the . occasionally , We have to feature in 0 To 1 Between , At this point, we can only use normalization .

3.1.3 neural network

1） Numerical problems

normalization / Standardization can avoid some unnecessary numerical problems . The order of magnitude of the input variable does not cause numerical problems , But in fact, it's not so difficult to cause . because tanh The nonlinear interval of is about [-1.7,1.7]. It means making neurons work ,tanh( w1x1 + w2x2 +b) Inside w1x1 +w2x2 +b The order of magnitude should be 1 （1.7 The order of magnitude ） about . In this case, the input is larger , It means that the weights have to be smaller , A larger , A smaller one , Multiply the two , And that leads to numerical problems .

2） Solving the problem requires

a. initialization ： In initialization, we want each neuron to initialize to a valid state ,tanh Function in [-1.7, 1.7] There is good nonlinearity in the range , So we hope that the input of the function and the initialization of the neuron can be in a reasonable range so that each neuron is effective at the beginning .

b. gradient ： To input - Cryptic layer - Output such three layers BP For example , We know that for input - The gradient of hidden layer weights is 2ew(1-a^2)*x In the form of （e It's the error ,w It's the weight from the hidden layer to the output layer ,a It's the value of the neurons in the hidden layer ,x It's input ）, If the order of magnitude of the output layer is very large , Can cause e It's an order of magnitude , Empathy ,w In order to make the hidden layer （ The order of magnitude is 1） Reflected in the output layer ,w It's going to be big , Plus x If it's too big , We can see from the gradient formula that , Multiply the three , The gradient is very big . This will bring numerical problems to the update of gradient .

c. Learning rate ： from （2） in , You know, the gradient is very large , The learning rate has to be very small , therefore , Learning rate （ The initial value of learning rate ） The selection needs to refer to the range of input , It's better to normalize the data directly , In this way, the learning rate does not have to be adjusted according to the data range . The weight gradient from hidden layer to output layer can be written as 2ea, The weight gradient from input layer to hidden layer is 2ew(1-a^2)x , suffer x and w Influence , The order of magnitude of each gradient is different , therefore , They need different orders of magnitude of learning rates . Yes w1 Appropriate learning rate , Maybe relative to w2 It's too small for me , If it is suitable for use w1 Learning rate of , It will lead to w2 Step very slowly in the direction , It takes a lot of time , And it's suitable for w2 Learning rate of , Yes w1 It's too big for me , No search for w1 Solution . If you use a fixed learning rate , And the data is not normalized , The consequences can be imagined .
 

3.2 Which algorithms in machine learning can not be normalized

Probability models don't need to be normalized , Because they don't care about the value of variables , It's about the distribution of variables and the conditional probabilities between variables . image svm、 Optimization problems such as linear regression require normalization . The decision tree belongs to the former . Normalization is also one of the necessary abilities to improve the application ability of the algorithm .

Is there any measurement of distance in the model algorithm , There is no measure of the standard deviation between variables . such as decision tree Decision tree , He used the algorithm, which did not involve any distance and other related , So when making a decision tree model , There is usually no need to standardize variables .

---

Four 、 The relationship between different normalization and different activation functions

4.1 sigmoid function

First of all Sigmoid For the activation function as an example ,Sigmoid The image of the function , The formula is as follows ：

 

Z Type update

Of course, this is the case for the first floor , After the activation function of the first layer Sigmoid After output , All output values range from [0,1] Between , That is, they are greater than 0, So the second floor in the back 、 The third floor to the last floor , In back propagation , Because of the input x  The symbols are all positive , Will appear Z Type renewal phenomenon , Make the network convergence speed very slow , This is it. Sigmoid Problems caused by non-zero mean function . So for Sigmoid In terms of functions , The first 2、3 To the last layer of neural network , Exist Z Type update problem , For zero averaging of input data , Can avoid the first layer of neural network Z Type update problem .

for fear of Z Type update , Zero the input , In this way, some input will be positive and negative doped input , Every ω  Gradient symbols and inputs for x  relevant , It won't be all the same , It won't be Z Type updated .

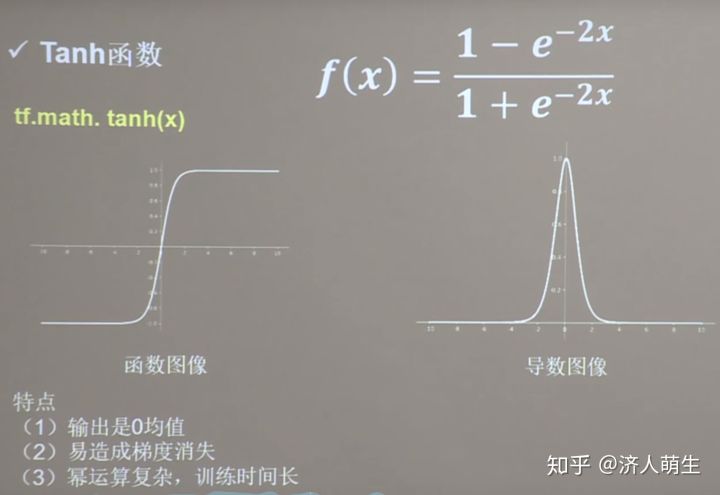
4.2 tanh function

tanh Function is also one of the classical activation functions , Function image , The formula is as follows ：

4.3 ReLU function

ReLU It is the most common activation function at present , Function image 、 The formula is as follows ：

---

5、 ... and 、 Some examples

5.1 Must logistic regression be standardized ？

It depends on whether our logistic regression is regular . If you don't use regular , that , Standardization is not necessary , If you use regular , Then standardization is necessary . Because when regular is not used , Our loss function only measures the difference between the prediction and the reality , Plus regular , In addition to measuring the gap above, our loss function , Also measure whether the parameter value is small enough . The magnitude of the parameter value, or the magnitude level, is related to the numerical range of the feature .

for instance , We use weight to predict height , Weight use kg When measuring , The trained model is ： height = weight *x ,x These are the parameters we have trained . When we weigh in tons ,x The value of will be expanded to the original 1000 times .

If the numerical range of different characteristics is different , There are plenty of them 0 To 0.1, There are plenty of them 100 To 10000, that , The parameter size level corresponding to each feature will also be different , stay L1 When regular , We simply add the absolute values of the parameters , Because they have different size levels , It will lead to L1 Finally, it will only work on parameters with large levels , Those small parameters are ignored .

If not regular , So what are the benefits of standardization for logistic regression ？ The answer is good , After standardization , The size of the parameter value we obtained can reflect the different characteristics of the sample label Contribution of , It is convenient for us to conduct feature screening . If there is no standardization , You can't filter features like this .

Are there any precautions for standardization ？ The most important thing to note is to split test Set , Don't standardize on the whole data set , Because that will test The information of the set is introduced into the training set , It's a very easy mistake ！

5.2 PCA Need standardization ？

Let's take a look at , If we will predict the variables of house prices , use PCA Methods to reduce dimensions , Will it have an impact on the results . We see that before standardization , One component can explain 99% The change of the variables of , And the standardized component explains 75% The change of . The main reason is that without standardization , We give too much weight to living space , It's the result .

5.3 Kmeans,KNN Need standardization ?

Kmeans,KNN Some distance related algorithms , Or clustering , We need to standardize the variables first .

　　 give an example ： We will 3 There are two types of cities , Variables include area and education level ; The three cities are like this ：

　　 City A, It's quite large , But robberies happen all day , Low education ;
　　 City B, The area is also very large , Good law and order , Highly educated ;
　　 City C, Medium size , Public security is also very good , Education is also very high ;

 

　　 If we don't do Standardization , If you do the clustering model directly ,A Cities and B The cities are divided , Do you think , A city with good public security and a whole city of theft and robbery are separated together , It's a bit against common sense .

Reference link ：

Standardization and normalization - nxf_rabbit75 - Blog Garden (cnblogs.com)

normalization （Normalization）、 Standardization （Standardization） And centralization / Zero mean value （Zero-centered） - Simple books (jianshu.com)

Several common normalization methods in machine learning and their reasons _UESTC_C2_403 The blog of -CSDN Blog _ Range normalization

normalization 、 Standardization 、 Zero mean effect and difference - You know (zhihu.com)

The role of neural network image input zeroing _wtrnash The blog of -CSDN Blog _ Zero mean value