Codeforces Round ＃802 (Div. 2)

C topic -Helping the Nature

Ideas

• Direct thinking ： Make each adjacent tree the same height . It can only be done for each adjacent tree , Process one of the prefixes or suffixes according to size , The same height is the smaller of the two , And none of these processing sequences can be less .
• Idea of difference （ turn ）：
  among $d_1=a[1]-a[0]$, among $a[0]=0$

When I see the interval operation, I think of prefix and difference . It belongs to the common routine

#include <bits/stdc++.h>
using namespace std;
#include<stack>
#define int long long
signed main()
{
    
    int t;
    cin >> t;
    for(int i = 0;i<t;i++)
    {
    
        int n;
        cin >> n;
        int a[n];
        for(int k = 0;k<n;k++) cin>>a[k];
        int ans = 0;
        int temp = a[n - 1];
        for(int k = n - 1;k>=1;k--)
        {
    
            if(a[k] - a[k - 1] >= 0)  // The suffix is subtracted to make it equal to the prefix 
            {
    
                ans += (a[k] - a[k - 1]);
                temp -= (a[k] - a[k - 1]);
            }
            else
            {
    
                ans += (a[k - 1] - a[k]);
            }
        }
        cout << ans + abs(temp) << endl;
    }
    system("pause");
}

D topic -Helping The Nature

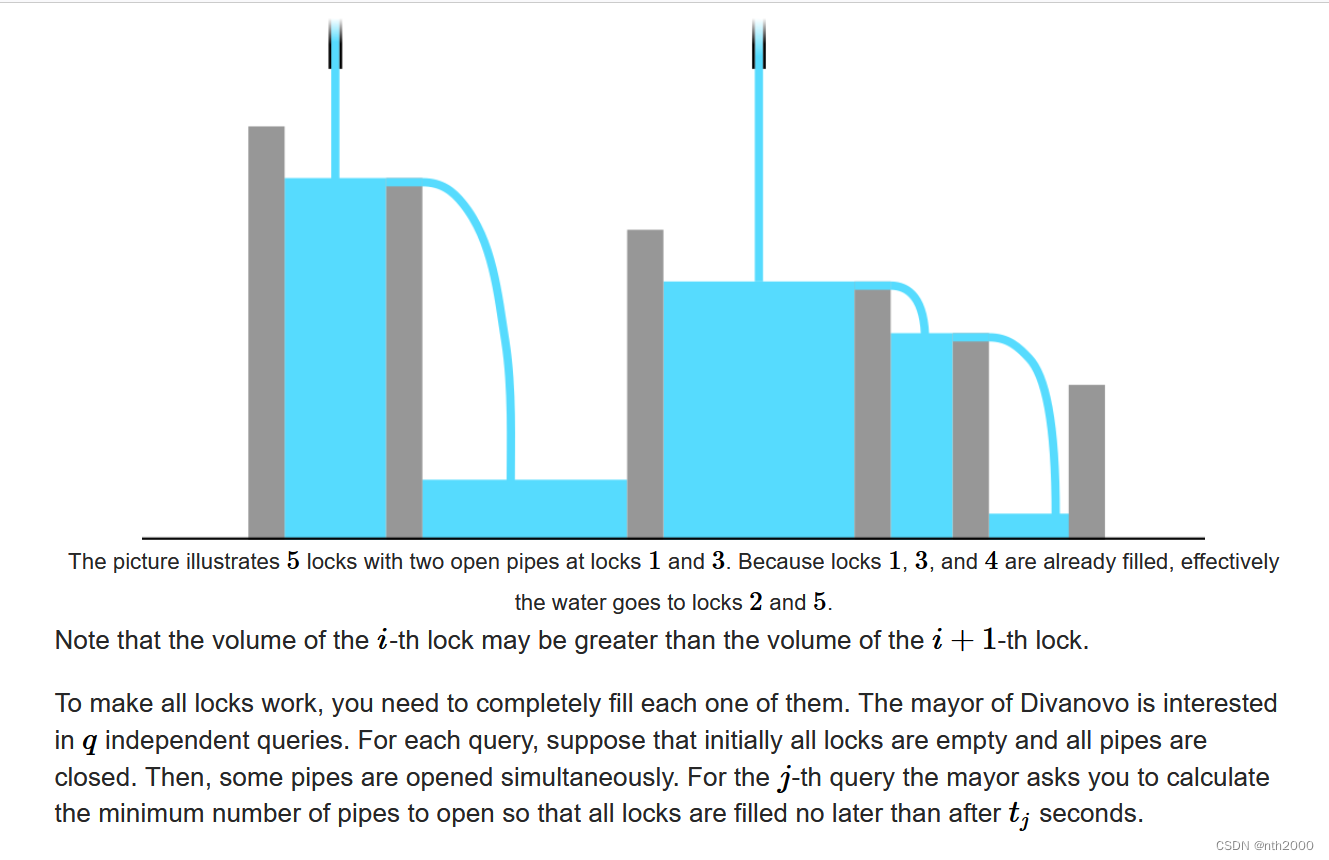
Ideas

• The necessary condition is to reduce the search space
• Find out if it can meet DP

set up $DP[i]$, Deal with the second i individual lock, front i individual lock All on , And fill it up i individual lock The shortest time needed .guess:

• Ruodi i individual lock Can be in front i-1 individual lock Before or just before the time of filling , be $DP[i]=DP[i-1]$
• otherwise , front i-1 individual lock Spilled water and the i individual lock The water in the pipes will mix with each other . It can be regarded as the former i Two pipes forward i individual lock Water injection . Time required $\lceil \frac{sum(v[1:i])}{i}\rceil$

therefore $$DP[i]=max(DP[i-1],\lceil \frac{sum(v[1:i])}{i}\rceil )$$
For each query, The necessary condition is $t_{query}>=dp[n]$. In such a period of time , If take q A pipe , It is guaranteed that there will be sufficient time to q One full of .

• If before opening q There are two pipes $dp[n]$ All the reservoirs have been filled up within the time , be q The conditions must be satisfied . And there must be $t_{query}\cdot q\ge dp[n]\cdot q\ge sum(v[1:n])$
• Otherwise, it can be regarded as before q The pipeline is filled with water at the same time , Rate mixing . Therefore, it is necessary to ensure that $t_{query}$ In time , With q rate , Can fill the reservoir , Also have ：$t_{query}\cdot q\ge sum(v[1:n])$

So given q, Just checking
$$t_{query}\cdot q\ge sum(v[1:n])$$ Whether it is satisfied or not is enough . Find the smallest one q that will do .

#include <bits/stdc++.h>
using namespace std;
#include<stack>
#define int long long
signed main()
{
    
    int n;
    cin >> n;
    int v[n];
    int prev[n + 1];
    prev[0] = 0;
    for(int i = 0;i<n;i++) 
    {
    
        scanf("%ld",&v[i]);
        prev[i + 1]  = prev[i] + v[i];
    }
    int dp[n + 1];
    dp[1] = v[0];
    for(int i = 2;i<=n;i++) dp[i] = max(dp[i - 1],(long long)ceil((double)prev[i] / i));
    int q;
    cin >> q;
    for(int i = 0;i<q;i++)
    {
    
        int t;
        scanf("%ld",&t);
        if(t < dp[n]) printf("-1\n");
        else   // Find the first one greater than or equal to ceil(prev[n]/t) Of prefixsum The sum of the 
        {
    
            t = (int)ceil((double)prev[n]/t);
            printf("%ld\n",t);
        }
    }
    system("pause");
}