图的基本概念以及相关定义

先来看几个单词：

1.

2.

3.

 

4.

  

再来说下面几个概念：

        1.图：

        顶点的有穷非空集合和顶点之间边的集合组成，通常表示为G=(V,E),G表示一个图，V表示顶点的集合，E表示边的集合

        2.无向边与有向边：

                无向边：比如从顶点v1到v2的边没有方向，则称这条边为无向边，用无序偶对(v1，v2)表示

                有向边：从顶点v1到v2有有方向，则称这条边为有向边，也成为弧arc，用有序偶对(v1,v2)表示，其中v1表示弧尾，v2表示弧头，注意(v2,v1)与(v1,v2)是两个不同的方向，也就是是两条不同的有向边

        3.有向图与无向图

                无向图：图中任意两个顶点之间都是无向边

                

                有向图 ：任意两点之间的边都是有向边

                

        4. 无向完全图与有向完全图

                无向完全图：任意两个顶点之间都存在边，含有n个结点的无向完全图有n(n-1)/2条边

                

                有向完全图：在有向图中，任意两个顶点之间都存在方向互为相反的两条弧。含有n个结点的有向完全图含有n(n-1)条边

                

         

5.一些其他的基础定义

        

         

              下面说一下入度与出度：

                         

                对于A来说，如果把A当成头弧，入度就为2，从B->A,C->A

                如果把A当成弧尾，出度就为1,A->D

                弧的数量等于各顶点出度和，等于各顶点入度和 

         

 6.连通图

         在无向图中，任何两个顶点都是互通的，也就是可以到达的，就是连通图

        

        左边不是连通图，右边是

        下面说一下连通图生成树

                首先它是一个极小的连通图子图，它含有图中全部n个结点，但是只有足以构成树的n-1条边

        

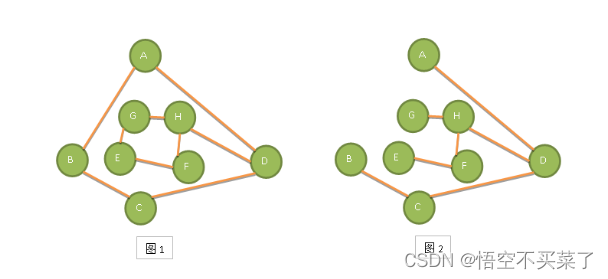
        图1有n个顶点，n条边，不是连通图生成树，图 2是，注意首先必须是连通图