Online notes on Mathematics for postgraduate entrance examination (8): Kego equations, eigenvalues and eigenvectors, similarity matrix, quadratic series courses

Video link ：https://www.cctalk.com/m/program/1629431535446012

Eigenvalues and eigenvectors

Inverse matrix multiplication and similarity are used to find eigenvalues

The rank is 1 Matrix , The characteristic value is n-1 individual 0 And a tr(A)（ The sum of the main diagonals ）

The sum of the elements in each row is the same , The eigenvalues are the sum ; The eigenvalue also satisfies f(A)=0

Trace is the sum of diagonal lines , It is also the sum of eigenvalues ;f(A)=0 What we get is the value of all eigenvalues , But not all eigenvalues

The eigenvalues are multiplied by the values of the determinant

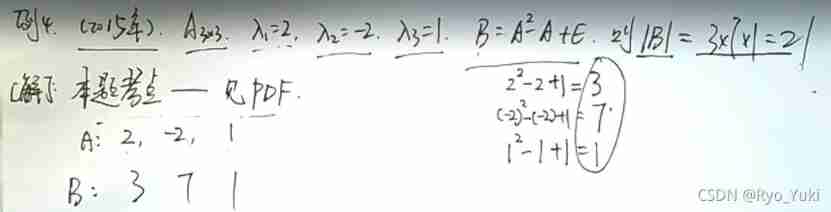
The adjoint trace is the sum of algebraic cofactors at diagonal positions

The eigenvalue ：A^*=|A|/λ

The eigenvalue corresponds to an eigenvector ; But there is no multiple relationship between eigenvalue and eigenvector ;

Characteristic polynomials must be zeroing polynomials

Similarity matrix and similarity diagonalization

P^-1AP=B, representative A And B be similar

A matrix similar to a diagonal matrix must be similarly diagonalized , And the eigenvalues are the same

The two matrices are similar , trace 、 Value of determinant 、 The characteristic values must all be equal ; Still can not judge , use r(A-λE)（ Necessary condition ） To do the elimination

Similarly diagonalized matrices have the same eigenvalues

When A The rank one matrix is ,A Can be similarly diagonalized with A The trace of is not 0 Equivalent

A rank one matrix can be decomposed into a column multiplied by a row , The trace of the matrix is the number calculated by multiplying a row by a column in another position

According to similar definitions , Use diagonal matrix to calculate

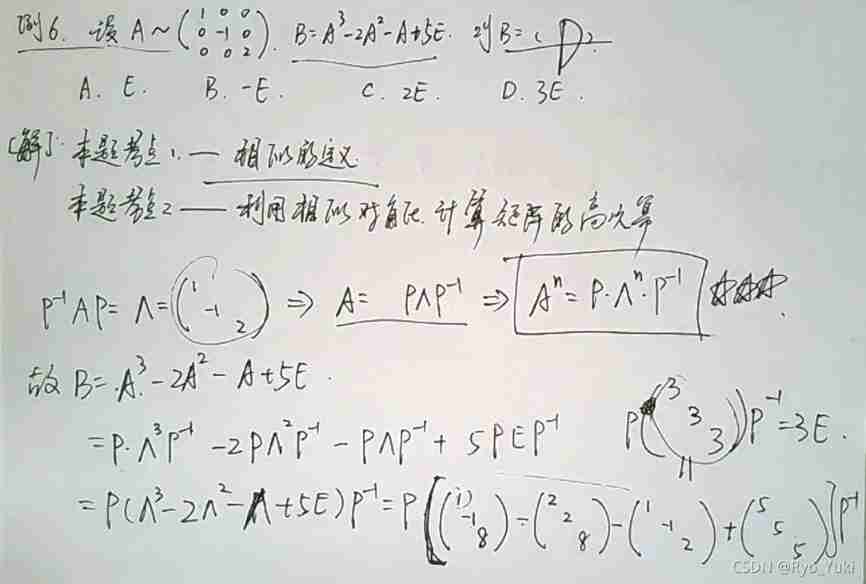
Of course , use 1、-1、2 The three eigenvalues are respectively represented by f(A) Calculate , It can also be calculated that the eigenvalue of the corresponding matrix is 3、3、3

The difference between no solutions and infinite solutions ： No solution requires that the right side is not 0, Infinite solutions require that the right side be 0

Real symmetric matrix

The transpose of a real symmetric matrix is equal to itself ; The matrix of a real antisymmetric matrix is the inverse of itself ; A real symmetric matrix can be similarly diagonalized by an orthogonal matrix , namely Q^-1AQ=E

The characteristic values are identical <–> Two real symmetric matrices are similar ; A method for computing eigenvalues with real symmetric matrices

A real symmetric matrix must be similarly diagonalized --> The number of nonzero eigenvalues is exactly r(A)

(B^T)^-1= (B^-1)^T

Eigenvalues and eigenvectors

Column vector groups are linearly correlated , There must be |A|=0, One eigenvalue is 0; The coefficient of inverse matrix multiplication is often the solution

Application of orthogonal matrix formula

The title continues

Use similarity to transform the research object , Be careful not to forget AQ=QB The step of transformation ;Q^-1AQ=B Plug in M^-1BM=∧, To get the invertible matrix P by QM

Use similarity to transform the research object , The unknown matrix can be transformed into a known matrix to calculate the eigenvalue

Similar traces are the same 、 The determinant is the same 、 The characteristics are the same ; Find the invertible matrix to make it similar , In general, each invertible matrix is obtained P₁、P₂, Simultaneous

A real symmetric matrix must be similarly diagonalized , So the number of nonzero eigenvalues is equal to the rank , Non full rank must have eigenvalue 0, The eigenvectors must be orthogonal

Real symmetric matrices are orthogonal to each other , There are eigenvalues and corresponding eigenvectors , Inverse real symmetric matrix A You can use the following method directly , Work out the result , Pretending on the test paper is still calculated in the old way

details ： Only when the same eigenvalue has two linearly independent eigenvectors can it be deduced that it is a double eigenvalue ; The sum of the elements in each row is 3, Eigenvalues have 3; There are eigenvalues and corresponding eigenvectors , Inverse real symmetric matrix A You can use the above solution directly

Aⁿ=P∧ⁿP^-1, Through similar diagonalization, it is transformed into a diagonal matrix n Power ; The above method cannot be used for non real symmetric matrices , The inverse must be found

Another kind of true topic in ancient times Aⁿ Test method ,

The method of undetermined coefficient is used to calculate the eigenvalue and eigenvector ; Orthogonal matrix Q Of Q^T Namely Q^-1, namely Q^TAQ=∧, Namely Q^-1AQ=∧; Real symmetric matrix from different eigenvalues （ Different values ） The eigenvector of a must be orthogonal , Irrelevant eigenvectors belonging to the same eigenvalue are not necessarily orthogonal

Add eigenvectors belonging to the same eigenvalue , Still eigenvectors ; Add eigenvectors belonging to different eigenvalues , Not eigenvectors

The eigenvector corresponding to a single eigenvalue is a straight line , The eigenvector corresponding to two eigenvalues is the whole plane ; Three different eigenvalues , When only one vector is known , The other two eigenvectors cannot be solved directly by orthogonality （ In the lower right corner ）

Standardization of quadratic form and positive definite quadratic form

just （ negative ） Inertia index means that the eigenvalue is positive （ negative ） The number of ; adopt |A-λE|=0 Find out the value of the characteristic value

21 Three years is the real problem

Positive definite matrix discrimination of concrete matrix ： The order principal and the subunits （ In the top left corner 1 To n rank ） Is greater than 0, We can deduce that it is a positive definite matrix ; A positive definite matrix must be a real symmetric matrix , All eigenvalues are positive

The coefficient of the standard form is the eigenvalue ; The eigenvector is multiplied by k, Does not change the characteristic value

In order to prevent irreversible transformation of the prepared quadratic form , Take apart to avoid mistakes

Equivalent 、 be similar 、 The difference between contracts

Similarity must be equivalent , The contract must be equivalent , But the opposite is not true ; Similarity is not necessarily related to contract , contract ： The positive and negative inertia indices are the same + Homosymmetry or homoasymmetry , be similar ： The eigenvalue corresponds to the eigenvector

When AB Are real symmetric matrices ,AB Similarity can lead to AB contract ; But the contract matrix does not require real symmetry , But it requires the same symmetry

The positive and negative inertia indices correspond to the same , Two matrix contracts ; From the positive and negative of determinant, we can see the positive and negative of eigenvalue

Without special skills , Calculate eigenvalues , If the eigenvalues are completely equal, they are similar （ No trace is alike ）, When the positive and negative inertia indices are equal, the contract is

Under the condition of real symmetric matrix , Similar contracts are necessary , The positive and negative inertia indices are the same

One quadratic form is transformed into another quadratic form , Both contracts

Quadratic problems

Orthogonal transformation is caused by Q^T=Q^-1, Implication AB be similar , The same old sites , The determinant is the same

When calculating parameters by reversible transformation , The nature of the problem , Only through positive and negative inertia index