当前位置:网站首页>[Supplementary Questions Diary] [2022 Niu Ke Summer Multi-School 4] A-Task Computing
[Supplementary Questions Diary] [2022 Niu Ke Summer Multi-School 4] A-Task Computing
2022-08-05 15:03:00 【cls1277】
Pro
https://ac.nowcoder.com/acm/contest/33189/A
Sol
先看m=2的情况,It is easy to list two equations: w 1 + w 2 × p 1 w_1+w_2\times p_1 w1+w2×p1和 w 2 + w 1 × p 2 w_2+w_1\times p_2 w2+w1×p2,Suppose the former is larger,即1在2的前面,The simplified formula is :
p 2 − 1 w 2 ≤ p 1 − 1 w 1 \frac{p_2-1}{w_2} \leq\frac{p_1-1}{w_1} w2p2−1≤w1p1−1,But in fact, it is not a problem to not come out of this formula,Because in order to avoid precision problems, it has to be multiplied back when writing overloads.
Then there is a proof(or guessing)This conclusion can be extended to m > 2 m>2 m>2的情况
After greedy sorting according to this method,就可以考虑dp的问题了
It can be obtained by extracting the common factor of the formula given in the question
原式 = w 1 + p 1 × ( w 2 + p 2 × ( w 3 + . . . ) ) 原式=w_1+p_1\times (w_2+p_2\times (w_3+...)) 原式=w1+p1×(w2+p2×(w3+...))
Therefore, the state transition equation can be obtained by reversing the order f i , j = m a x { f i + 1 , j , f i + 1 , j − 1 × p i + w i } f_{i,j}=max\{f_{i+1,j},f_{i+1,j-1}\times p_i+w_i\} fi,j=max{ fi+1,j,fi+1,j−1×pi+wi}
是不是有点像01背包了
Code
//By cls1277
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
#define Fo(i,a,b) for(LL i=(a); i<=(b); i++)
#define Ro(i,b,a) for(LL i=(b); i>=(a); i--)
#define Eo(i,x,_) for(LL i=head[x]; i; i=_[i].next)
#define Ms(a,b) memset((a),(b),sizeof(a))
#define endl '\n'
const LL maxn = 1e5+5;
LL n, m;
double f[maxn][25];
struct Node {
LL w;
double p;
}a[maxn];
bool operator < (const Node &x, const Node &y) {
return (x.w+y.w*x.p>=y.w+x.w*y.p);
}
inline LL read() {
LL x = 0, f = 1;char c = getchar();
while (!isdigit(c)) {
if (c == '-')f = -f;c = getchar(); }
while (isdigit(c)) x = (x << 1) + (x << 3) + (c ^ 48ll), c = getchar();
return x * f;
}
int main() {
// ios::sync_with_stdio(false);
// cin.tie(nullptr);
#ifdef DEBUG
freopen("data.txt","r",stdin);
#endif
n=read(); m=read(); // cin>>n>>m;
Fo(i,1,n) a[i].w=read(); //cin>>a[i].w;
Fo(i,1,n) {
LL x; x=read(); //cin>>x;
a[i].p = x*1.0/10000;
}
sort(a+1, a+n+1);
Ro(i,n,1) {
Fo(j,1,m) {
f[i][j] = max(f[i+1][j], f[i+1][j-1]*a[i].p+a[i].w);
}
}
printf("%.16lf",f[1][m]);
return 0;
}
边栏推荐
- [SQL Interview Questions You Shouldn't Miss--2022]
- Study Notes 251—XMind Shortcuts Summary
- Oracle自治事务详解
- 请指教同花顺究竟怎么开户?在线开户安全么?
- [Navicat] Navicat export database table design document specific instructions
- Generate a .pkl file and read the content of the .pkl file
- 2022最新综述 | 面向大规模场景的小目标检测:综述和 benchmark
- 概率论基础 - 3 - 方差
- 概率论基础 - 9 - 中心极限定理
- 统计遗传学:第四章,GWAS分析
猜你喜欢
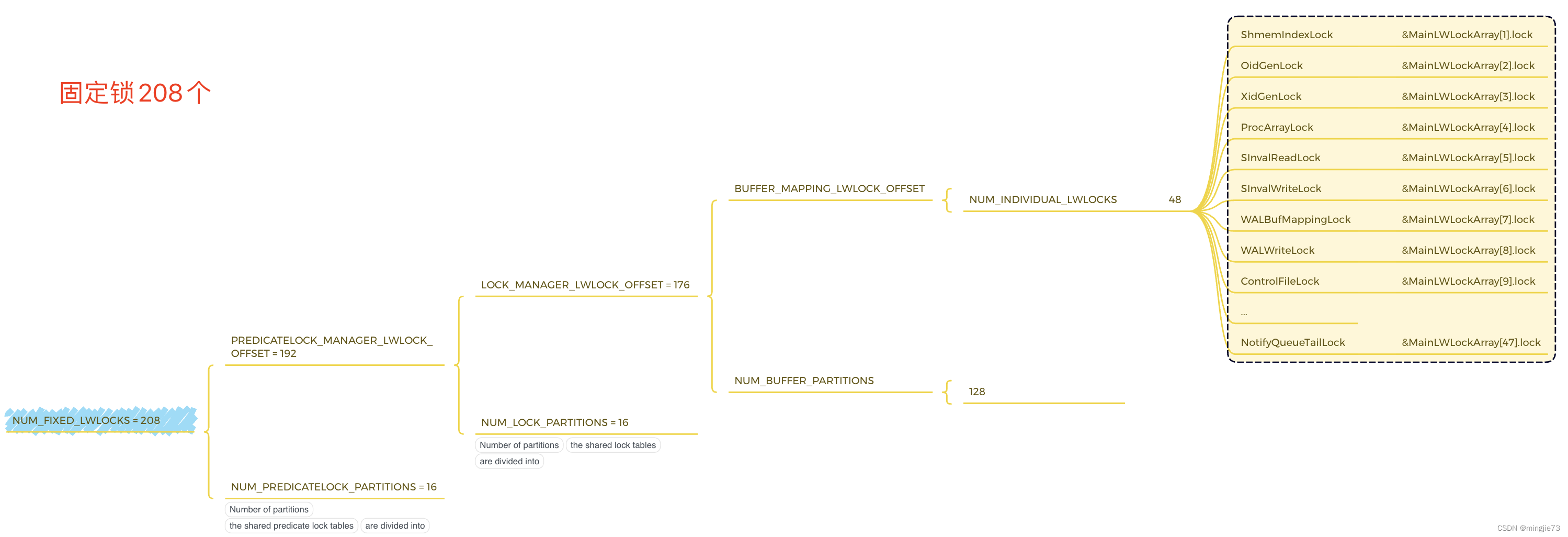
Postgresql源码(67)LWLock锁的内存结构与初始化

PR视频剪辑教程--视频特效和转场

Score-CAM|用kernel加权解释CNN的预测结果
GIS、多场景加载、溶解特效等功能首次公开,全网免费调用!

刷题《剑指Offer》day09

Blow it up!The 1658-page trial summary of Ali Gaogong and 18 architects that took 57 days to integrate is too fragrant

playwright录制脚本

自媒体爆文如何写作?学会这4点,能让你快速提升阅读量
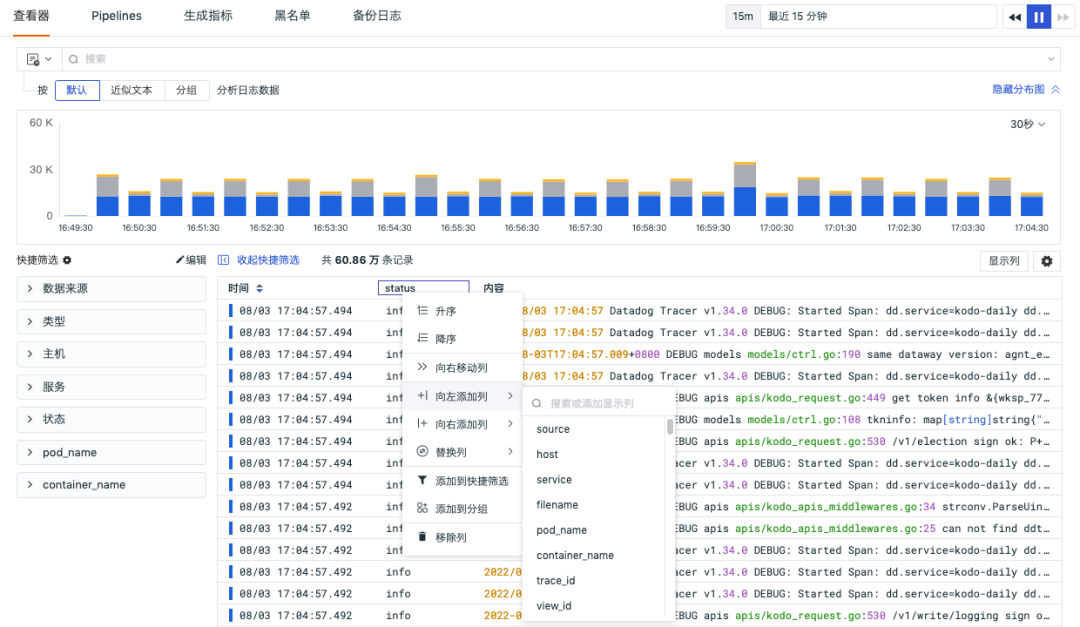
Observation cloud product update|DCA web terminal is online; new global viewer auto refresh configuration; new global blacklist function; new custom function menu, etc.
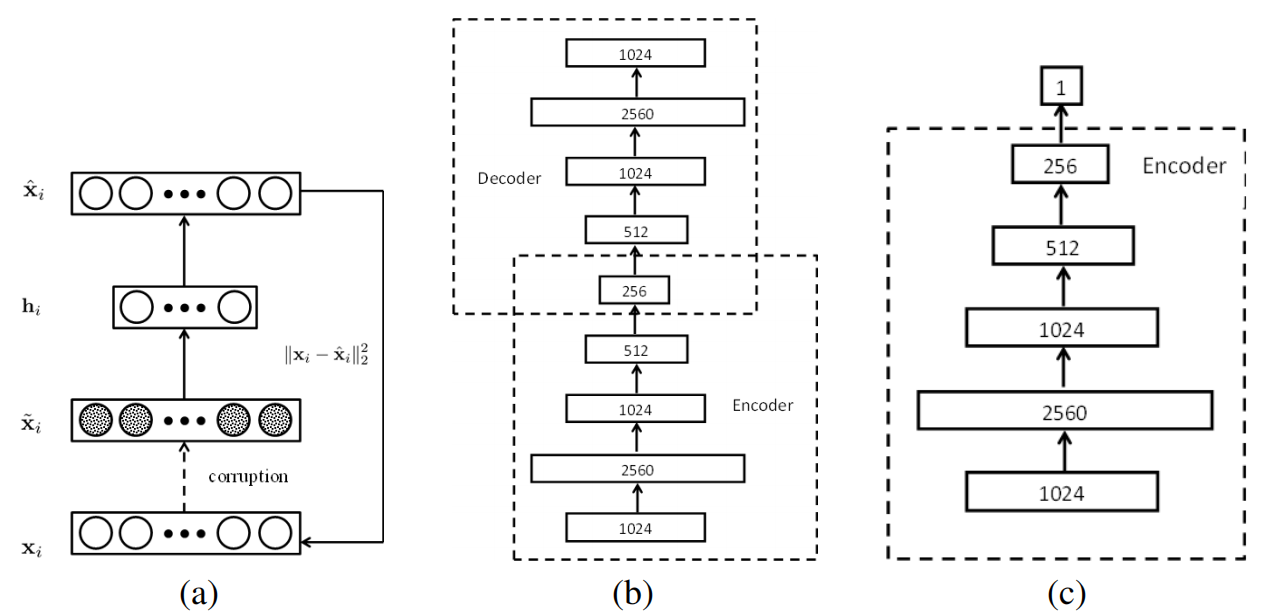
学习用于视觉跟踪的深度紧凑图像表示Learning a Deep Compact Image Representation for Visual Tracking
随机推荐
An in-depth long article discusses the simplification and speedup of JOIN operations
环境文件复制
GIS、多场景加载、溶解特效等功能首次公开,全网免费调用!
【绝对不要错过的sql面试题--2022年】
十五个AI图像放大工具
抖音自媒体运营的5个技巧,让你的账号快速涨粉
Voice Chat App Development - How Developers Do Code Analysis
请指教我想今天开户,可以么?手机开户安全么?
Fundamentals of Probability - 11 - Gaussian Distribution / Normal Distribution
playwright recording script
兆骑科创高层次人才创业赛事活动,创新创业人才引进平台
垃圾回收机制
生成.pkl文件,读取.pkl文件的内容
map 和 forEach 的区别
数据大屏rem适配方案
消失的遗传力的进一步剖分及应用
学习笔记251—XMind快捷键汇总
【kali-Metasploit】Armitage常见问题:sudo权限、连接不到数据库、service not found
华为分析&联运活动,助您提升游戏总体付费
Read it all!Adapter technology in NLP