当前位置:网站首页>HDU - 2586 How far away ? (multiply LCA)
HDU - 2586 How far away ? (multiply LCA)
2022-07-23 20:53:00 【WA_ automata】
HDU - 2586 How far away ?
Multiplication method Preprocessing (nlogn) + Inquire about (logn)
The key is to understand binary patchwork How is it reflected here
namely x,y After taking off from the same height at the same time , stay f[x][0]!=f[y][0] Under the constraint of The most steps we can jump... After jumping x,y That's it. LCA The lower floor of
Suppose we know x,y The starting point is 1 layer
LCA The next floor is 12 layer
Then the maximum number of steps you can jump t = 12-1 = 11 = (1011)2 = At most 2^3 + 2^2 + 2^0 Step
So we enumerate from large to small k Make us just jump 11 Step without jumping more than 12 Step
But in fact, we don't know to jump 11 Step , So we can pass f[x][0]!=f[y][0] To achieve
namely f[x][ in total >=12 Step ] = f[y][ in total >=12 Step ] Then don't jump ( No patchwork 2^k)
f[x][ in total <12 Step ] != f[y][ in total <12 Step ] Then jump ( Put together 2^k)
Preprocess each point to go up 2^k Who is the father of step's node
f[i][j] from i Start walking up 2^j The node that can be reached in one step 0<=j<=logn
1
/ \
2 3
/ \
4 5
/ \
6 7
f[6][0] = 4
f[6][1] = 2
f[6][2] = An empty set
j=0 f[i][j] = i Parent node
j>0 f[i][j-1]
i → mid → t
2^j-1 2^j-1
f[i][j-1] f[i][j]
mid = f[i][j-1]
t = f[i][j]
be f[i][j] = f[mid][j-1] = f[f[i][j-1]][j-1]
depth[i] Expressing depth / The layer number
1
/ \
2 y
/ \
4 5
/ \
x 7
step 1 Jump the two points to the same floor hold x Jump to and y Same floor
Binary patchwork 2^0 ~ 2^k t
give an example 2^0 ~ 2^4 11
1 2 4 8 16 11 Binary system
16>11 0
8<11 t = 11-8 = 3 1
4>3 0
2<3 t = 3-2 = 1 1
1>=1 t = 1 1
Binary system (1011)2
depth(x) - depth(y)
from x Jump to the y
from x jump 2^k The depth of the point after the step depth(f[x][k]) >= depth(y) when You can continue to jump
step 2 stay depth(x)==depth(y) after Jump up together 2^k(for k in [log(n),1]
situation 1 x==y Then the point is x and y The latest public ancestor of
situation 2 x!=y That is, they are on the same level but different
Then continue to let the two points jump up at the same time Jump to the next level of their nearest common ancestor
1 1
/ \ / \
2 y x y
/ \ / \
4 5 4 5
/ \ / \
x 7 6 7
why The next level of the nearest common ancestor not Recent public ancestor ?
Convenient judgment
If f[x][k] == f[y][k] <=> f[x][k] or f[y][k] yes x and y A common ancestor of But it's not necessarily recent
Take a chestnut
here f[x][1] == f[y][1] = node 2 yes x and y A common ancestor of But not the nearest public ancestor 4
, But because we are pieced together from big to small , If the end condition of patchwork is f[x][k] == f[y][k]
, Then it will stop at the common ancestor 2 Not the nearest public ancestor 4
1
/ \
2 3
/ \
4 5
/ \ /
x y 8
Step one x Come first y Same floor f[x][0]!=f[x][0] And k Can fill 1 All of them have been filled in
Put constraints on it f[x][k] != f[y][k]
Think about why : Because the first appeared f[x][k] == f[y][k] The node of is only a public ancestor, but it cannot be guaranteed to be the nearest public ancestor
So as long as f[x][k] != f[y][k]
that x y I haven't jumped to the nearest public ancestor , And on the lower layer
Enumerate from big to small k
During enumeration
as long as f[x][k] != f[y][k]
that x y I haven't jumped to the nearest public ancestor , And on the lower layer , be x,y Updated to f[x][k] f[y][k]
In the process f[x][k] == f[y][k] when
Do not perform jump 2^k Step to f[y][k] The operation of
until k Enumerate until
After enumeration, we go to the next level of the nearest public ancestor
Binary patchwork 2^0 ~ 2^k t
there k The maximum is logn
t by x and y Reach the same height (depth( start )) - The depth of the nearest common ancestor -1(depth( The ancestors )-1)
give an example 2^0 ~ 2^4 2
1 2 4 8 16 2 Binary system
16>2 0
8>2 0
4>2 0
2=2 t = 2-2 = 0 1
1>0 0
1
/ \
2 3
/ \ \
4 5 8
/ \ \
x 7 9
1 \
/ \ y
2 3
/ \ \
4 5 8
/ \ \
x 7 y
In this case k=4 t=2(4(x,y Departure floor )-2(LCA The next layer ))[ adopt f[x][k] != f[y][k] constraint ]
1
/ \
x y
/ \ \
4 5 8
/ \ \
6 7 9
At this time, their nearest common ancestor is x or y Jump up one step
namely LCA = f[x][0] or f[y][0]
#include<bits/stdc++.h>
using namespace std;
typedef pair<int,int> PII;
const int N = 40010;
int f[N][16],d[N],dist[N];
vector<PII> g[N];
void bfs()
{
queue<int> q;
q.push(1);
d[1]=1;
while(!q.empty())
{
int u=q.front();q.pop();
for(auto &p:g[u])
{
int j=p.first,w=p.second;
if(d[j]) continue;
d[j]=d[u]+1;
dist[j]=dist[u]+w;
f[j][0]=u;
for(int k=1;k<=15;k++)
f[j][k]=f[f[j][k-1]][k-1];
q.push(j);
}
}
}
int lca(int x,int y)
{
if(d[x]>d[y]) swap(x,y);
for(int i=15;i>=0;i--)
if(d[f[y][i]]>=d[x])
y=f[y][i];
if(x==y) return x;
for(int i=15;i>=0;i--)
if(f[x][i]!=f[y][i])
x=f[x][i],y=f[y][i];
return f[x][0];
}
int main()
{
int T;cin>>T;
while(T--)
{
int n,m;cin>>n>>m;
for(int i=1;i<=n;i++) g[i].clear();
for(int i=1;i<=n-1;i++)
{
int a,b,c;cin>>a>>b>>c;
g[a].push_back({
b,c});
g[b].push_back({
a,c});
}
bfs();
for(int i=1;i<=m;i++)
{
int x,y;cin>>x>>y;
cout<<dist[x]+dist[y]-dist[lca(x,y)]*2<<endl;
}
}
return 0;
}
边栏推荐
猜你喜欢

Opencv image processing Laplace pyramid

高数下|三重积分的计算2|高数叔|手写笔记

【复数 重载运算符】

OpenLayers实例-Advanced Mapbox Vector Tiles-高级Mapbox矢量贴图

Lingo basic use

《迷失》stray工人帽子获得方法 工人安全帽在哪里?
现在完全不知道怎么同步
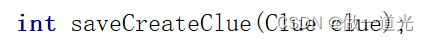
第3章业务功能开发(创建线索)

Unity解决动画不可用:The AnimationClip ‘XXX‘ used by the Animation component ‘XXX‘ must be marked as Legacy.

Addon plug-in 002 of CDR plug-in development - write an EXE program that can be run by double clicking in 1 minute
随机推荐
[PDD interview] analyze the activity of applications (cameras) in mobile phones
OpenIM重大升级-群聊读扩散模型发布 群管理功能升级
prime_series_level-1
Green-Tao 定理 (4): 能量增量方法
win7-vs2012下安装.net frame work 的过程图文详解
支付宝常用接口统一封装,可直接支付参数使用(适用于H5、PC、APP)
Interpretation of Flink catalog
Junior intern, ByteDance, after sharing, has been offered
OOM机制
【攻防世界WEB】难度四星12分进阶题:Confusion1
使用代码设置activity为透明
Educational codeforces round 132 A-D problem solution
Yiwen teaches you how to install MySQL
Cesium 键盘鼠标控制相机漫游(源码+原理讲解)
Visual slam learning | basic chapter 01
Now I don't know how to synchronize at all
哈希表、无序集合、映射的原理与实现
221. 最大正方形 ●● & 1277. 统计全为 1 的正方形子矩阵 ●●
第十二天:续第十一天(BGP相关知识)
MySQL(3)
