221. 最大正方形 ●● ＆ 1277. 统计全为 1 的正方形子矩阵 ●●

221. 最大正方形 ●●

描述

在一个由 ‘0’ 和 ‘1’ 组成的二维矩阵内，找到只包含 ‘1’ 的最大正方形，并返回其面积。

示例

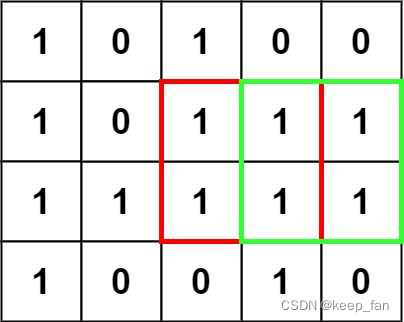
输入：matrix = [[“1”,“0”,“1”,“0”,“0”],[“1”,“0”,“1”,“1”,“1”],[“1”,“1”,“1”,“1”,“1”],[“1”,“0”,“0”,“1”,“0”]]
输出：4

题解

1. 暴力解法（超时）

要找到最大正方形的面积，首先需要找到最大正方形的边长，然后计算最大边长的平方即可。

暴力法是最简单直观的做法，具体做法如下：

• 遍历矩阵中的每个元素，每次遇到 1，则将该元素作为正方形的左上角；
• 确定正方形的左上角后，根据左上角所在的行和列计算可能的最大正方形的边长（正方形的范围不能超出矩阵的行数和列数），在该边长范围内寻找只包含 1 的最大正方形；
• 每次在下方新增一行以及在右方新增一列，判断新增的行和列是否满足所有元素都是 1。

---

• 时间复杂度：$O(mn\min (m,n{)}^2)$，其中 m 和 n 是矩阵的行数和列数。
  – 需要遍历整个矩阵寻找每个 1，遍历矩阵的时间复杂度是 O(mn)O(mn)。
  – 对于每个可能的正方形，其边长不超过 m 和 n 中的最小值，需要遍历该正方形中的每个元素判断是不是只包含 1，遍历正方形时间复杂度是 $O(\min (m,n{)}^2)$。
• 空间复杂度：$O(1)$。额外使用的空间复杂度为常数。

class Solution {
    
public:
    int maximalSquare(vector<vector<char>>& matrix) {
    
        int m = matrix.size();
        int n = matrix[0].size();
        int maxArea = 0;
        for(int i = 0; i < m; ++i){
    
            for(int j = 0; j < n; ++j){
    
                if(matrix[i][j] == '1'){
            	    // (i, j)为左上角坐标
                    int minLen = n+m;				    // 列上连续 1 的最小长度
                    for(int k = j; k < n; ++k){
    		    // 遍历每列
                        if(k - j + 1 > minLen) break;   // 当前列所在的行边长大于最小长度，跳出循环
                        int len = 0;				    // 记录该列连续 1 的个数
                        for(int l = i; l < m; ++l){
     
                            if(l-i+1 > minLen) break;	// 当前列边长大于最小长度，跳出循环
                            if(matrix[l][k] == '0') break;
                            ++len;  
                        }
                        maxArea = max(maxArea, min(len, k-j+1)*min(len, k-j+1));    // 遍历完一列之后，更新当前的最大面积，边长为 min(列长，行长)
                        minLen = min(len, minLen);      // 更新最小长度
                    }
                }
            }
        }
        return maxArea;
    }
};

2. 动态规划

1. dp[i][j] 表示 以 matrix[i][j] 为右下角时，只包含 1 的正方形最大边长。
2. 对第一行和第一列进行初始化，‘1’ 是边长置 1，否则为 0；
3. matrix[i][j] == '0'： dp[i][j] = 0；
matrix[i][j] == '1'：dp[i][j] = min(min(dp[i-1][j-1], dp[i-1][j]), dp[i][j-1]) + 1;
4. 从左往右，从上到下遍历。

---

• 时间复杂度：$O(mn)$，其中 m 和 n 是矩阵的行数和列数。需要遍历原始矩阵中的每个元素计算 dp 的值。
• 空间复杂度：$O(mn)$，其中 m 和 n 是矩阵的行数和列数。创建了一个和原始矩阵大小相同的矩阵 dp。
  由于状态转移方程中的 dp(i,j) 由其上方、左方和左上方的三个相邻位置的 dp 值决定，因此可以使用两个一维数组进行状态转移，空间复杂度优化至 O(n)。

class Solution {
    
public:
    int maximalSquare(vector<vector<char>>& matrix) {
    
        int m = matrix.size(), n = matrix[0].size(), maxLen = 0;
        vector<vector<int>> dp(m, vector<int>(n, 0));   
        // 边界条件处理
        for(int i = 0; i < m; ++i) if(matrix[i][0] == '1'){
    dp[i][0] = 1; maxLen = 1;}
        for(int j = 0; j < n; ++j) if(matrix[0][j] == '1'){
    dp[0][j] = 1; maxLen = 1;}
        for(int i = 1; i < m; ++i){
    
            for(int j = 1; j < n; ++j){
    
                if(matrix[i][j] == '1'){
    
                    dp[i][j] = min(min(dp[i-1][j-1], dp[i-1][j]), dp[i][j-1]) + 1;
                    maxLen = max(maxLen, dp[i][j]);
                }
            }
        }
        return maxLen * maxLen;
    }
};

1277. 统计全为 1 的正方形子矩阵 ●●

描述

给你一个 m * n 的矩阵，矩阵中的元素不是 0 就是 1，请你统计并返回其中完全由 1 组成的 正方形 子矩阵的个数。

示例

输入：matrix =
[
[0,1,1,1],
[1,1,1,1],
[0,1,1,1]
]
输出：15
解释：
边长为 1 的正方形有 10 个。
边长为 2 的正方形有 4 个。
边长为 3 的正方形有 1 个。
正方形的总数 = 10 + 4 + 1 = 15.

题解

动态规划

与 221. 最大正方形 ●● 类似，每次计算累加正方形个数和即可，以 (i, j) 为右下角的正方形个数即为最大边长值 dp[i][j]，注意处理边界条件时，(0,0) 不能重复处理。

class Solution {
    
public:
    int countSquares(vector<vector<int>>& matrix) {
    
        int m = matrix.size(), n = matrix[0].size(), sum = 0;
        vector<vector<int>> dp(m, vector<int>(n, 0));   
        for(int i = 0; i < m; ++i) if(matrix[i][0] == 1){
    dp[i][0] = 1; ++sum;}
        for(int j = 1; j < n; ++j) if(matrix[0][j] == 1){
    dp[0][j] = 1; ++sum;}
        for(int i = 1; i < m; ++i){
    
            for(int j = 1; j < n; ++j){
    
                if(matrix[i][j] == 1){
    
                    dp[i][j] = min(min(dp[i-1][j-1], dp[i-1][j]), dp[i][j-1]) + 1;
                    sum += dp[i][j];
                }
            }
        }
        return sum;
    }
};