Principle and Simulation of switching power supply buck circuit

The circuit principle diagram

• Buck circuit , Also known as step-down circuit , The characteristic is that the output voltage is lower than the input voltage . The input current is pulsating , The output current is continuous .

How it works

• When the switch tube Q1 The drive is high , The switch tube is on , Energy storage inductance L1 Magnetized , The current flowing through the inductor increases linearly , At the same time C1 Charge , Give load R1 Provide energy . The equivalent circuit is as follows ：
  
• When the switch tube Q1 The drive is at low level , Switch off , Energy storage inductance L1 Discharge through freewheeling diode , Linear reduction of inductive current , The output voltage depends on the output filter capacitor C1 Discharge and reduced inductive current maintenance , The equivalent circuit is as follows ：
  

Three working modes

CCM Mode

• Switch tube Q1 Conduction , according to KVL：$$V_{in}-L\frac{d{i}_L}{dt}-V_o=0,namelyL\frac{△i_L}{△t}=V_{in}-V_o\to L\ast △i_L=(V_{in}-V_o)\ast △t$$
• $△t$ by Q1 On time of ,$△t=T\ast D$,$T$ For duty cycle ,$D$ Is the duty cycle ：$$L△i_L=(V_{in}-V_o)TD$$
• Switch tube Q1 Turn off , according to KVL（ Ignore the on voltage drop of the diode ）：$$L\frac{d{i}_L}{dt}=V_{o}namelyL\ast △i_L=V_o\ast T(1-D)$$
• According to volt second balance ：$L△i_L=(V_{in}-V_o)\ast T\ast D=V_o\ast T(1-D)$
• Available ：$V_o=V_{in}\ast D$
• Usually when we design circuits , Often know the input and output voltage , So that we can go through $D=\frac{V_o}{V_{in}}$ To make sure CCM Duty cycle in mode .
• Load current I_o Relationship with inductive current
  • Analyze in one cycle , The load current is the average value of the current in a cycle .
  • The mathematical expression of the average value of the current ：$$I_{AV}=\frac{{\int }_0^{T}i(t)dt}{T}$$
  • That is, the area enclosed by the current function curve and time axis in a period divided by the period , Is the average value of the current .
  • According to the previous inductance current waveform , It is known that the area in a cycle is ：$$S=\frac{I_{Lmin}+I_{Lmax}}{2}T\ast D+\frac{I_{Lmin}+I_{Lmax}}{2}T\ast (1-D)=\frac{I_{Lmin}+I_{Lmax}}{2}T$$
  • therefore , The average current is $$I_o=\frac{S}{T}=\frac{I_{Lmin}+I_{Lmax}}{2}$$

BCM Mode

• contrast BCM Follow CCM The difference between ： It can be found that the minimum current of the inductance gradually decreases to 0, The working mode has gradually changed from CCM Gradient to BCM. According to volt second balance ：$$(V_{in}-V_o)\ast T\ast D=V_o\ast T(1-D)$$$$V_o=V_{in}\ast D$$
• Again , Analyze in one cycle , Output average current $I_o$: $$I_o=\frac{T\ast I_{Lmax}/2}{T}=\frac{I_{Lmax}}{2}$$

DCM Mode

• The circuit works in DCM In mode , Two conditions need to be met ：
  • The current flowing through the inductor at the beginning of magnetization and the end of degaussing is zero ;
  • The degaussing time of the inductor is less than the switch off time ;
• According to volt second balance ： $$(V_{in}-V_o)\ast T\ast D=V_o\ast T_d$$$$V_o=V_{in}\ast \frac{T_{on}}{T_{on}+T_d}$$
• Again , Analyze in one cycle , Output average current $I_o$: $$I_o=\frac{I_{Lmax}(T\ast D+T_d)}{2T}$$

The relationship between inductance value and working mode

• Give a picture
  
• Analyze the inductive current in one cycle ：$$I_o=\frac{(I_{Lmin}+I_{Lmax})\ast D\ast T}{2T}+\frac{(I_{Lmin}+I_{Lmax})\ast T_d}{2T}$$
• namely $$2T{I}_o=(I_{Lmin}+I_{Lmax})\ast (D\ast T+T_d)$$
• When Q The pipe is open : $$L\frac{d{i}_L}{dt}=V_{in}-V_o\to L\frac{I_{Lmax}-I_{Lmin}}{TD}=V_{in}-V_o$$
• namely $$I_{Lmax}=\frac{(V_{in}-V_o)\ast T\ast D}{L}+I_{Lmin}$$
• Into the above equation ：$$2T{I}_o=\left[I_{Lmin}+\frac{(V_{in}-V_o)TD}{L}+I_{Lmin}\right](TD+T_d)$$$$T_d=\frac{2TL{I}_o-2TDL{I}_{Lmin}-V_{in}{T}^2{D}^2+V_o{T}^2{D}^2}{2L{I}_{Lmin}+V_{in}TD-V_{o}TD}$$
• If you work in DCM Pattern , Then order $I_{Lmin}=0,T_d<T(1-D)$, namely $$\frac{2TL{I}_o-V_{in}{T}^2{D}^2+V_o{T}^2{D}^2}{V_{in}TD-V_{o}TD}<T(1-D)\to L<\frac{(V_{in}-V_o)TD}{2I_o}$$
• If you work in BCM Pattern , Then order $I_{Lmin}=0,T_d=T(1-D)$, namely $$\frac{2TL{I}_o-V_{in}{T}^2{D}^2+V_o{T}^2{D}^2}{V_{in}TD-V_{o}TD}=T(1-D)\to L=\frac{(V_{in}-V_o)TD}{2I_o}$$
• If you work in CCM Pattern , Then order $I_{Lmin}>0,T_d=T(1-D)$, namely $$I_{Lmin}=\frac{T{I}_o}{TD+T_d}-\frac{(V_{in}-V_o)TD}{2L}>0\to L>\frac{(V_{in}-V_o)TD}{2I_o}$$

Ideal design example

• Set the input voltage U_i=20V, Output voltage U_o=10V, Ripple voltage <1%,I_o=1A, Switch frequency f_s=100k, Try to design work in BCM The circuit of the mode meets the requirements .
• The calculation is as follows ：
  • Duty cycle ：$$D=\frac{U_o}{U_i}=\frac{10}{20}=0.5$$
  • Critical inductance of operating mode ：$$L_c=\frac{(V_{in}-V_o)TD}{2I_o}=\frac{(20-10)\ast 0.5}{2\ast 100k\ast 1}=25uH$$
  • Load resistance ：$$R_L=\frac{V_o}{I_o}=\frac{10}{1}=10\Omega$$
  • Output capacitance （ Don't consider ESR And transient overshoot voltage ） Calculation ：$$C_o=\frac{1}{8f_s}\ast \frac{△i}{△u}=\frac{1}{8\ast f_s}\ast \frac{I_{Lmax}-I_{Lmin}}{△u}=\frac{1}{8\ast 100k}\ast \frac{2-0}{10\ast 0.01}=25uF$$

saber Circuit simulation

Simulation circuit diagram

Several key device settings

• Analog switch tube ： stay saber Select... From the search results switch,analog SPST w/logic Enbl, Double click Add to schematic .

• Set parameters
  

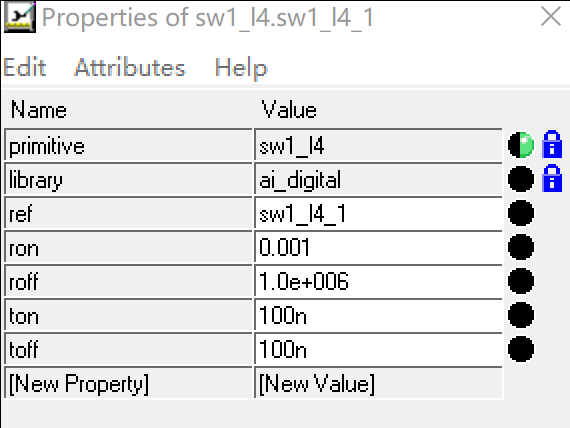
  • ron： Impedance when the switch is on , It can be set as the default value 0.001;
  • roff： Impedance when the switch is closed , It can be set as the default value 1M;
  • ton： Switch on time ;
  • toff： Switch off time ;

• Driving signal

  • After setting the switch tube , You need to give it a drive signal
    
  • freq： Drive signal frequency , Set here as 100k;
  • duty： Duty cycle , Set to 0.5;

• Other periods can be set by referring to the previously calculated values .

Simulation settings

Waveform analysis

• When the circuit starts simulation , The initial state of inductance and capacitance is 0, Go through an oscillating process , Reach a balance .
• Amplify the inductance current waveform , It can be seen that it works in BCM Pattern , Conform to the design .
• Amplify the output voltage , It can be seen that the ripple voltage meets the design requirements .
  

Closed loop control

• Compare with the above , We can find out , In open loop buck In circuit , The output voltage does not strictly follow the product of the input voltage duty cycle .
• In the actual circuit , The input power supply and output load fluctuate to some extent , The settings will change dramatically , These factors make the open-loop system unable to guarantee stable output , Therefore, feedback should be added to form a closed loop .
  
• Closed loop control method , At present, single closed-loop control is widely used , Most of them are closed-loop control schemes with negative voltage feedback , This is a linear control method , Simple control , The control algorithm adopts the classic PID control . By differential amplifier ,PI Regulator , as well as PWM Control composition .

Error amplifier （ Subtracter ）

• The negative phase input terminal is connected to the output voltage fed back , Positive phase input termination bandgap reference voltage .
  
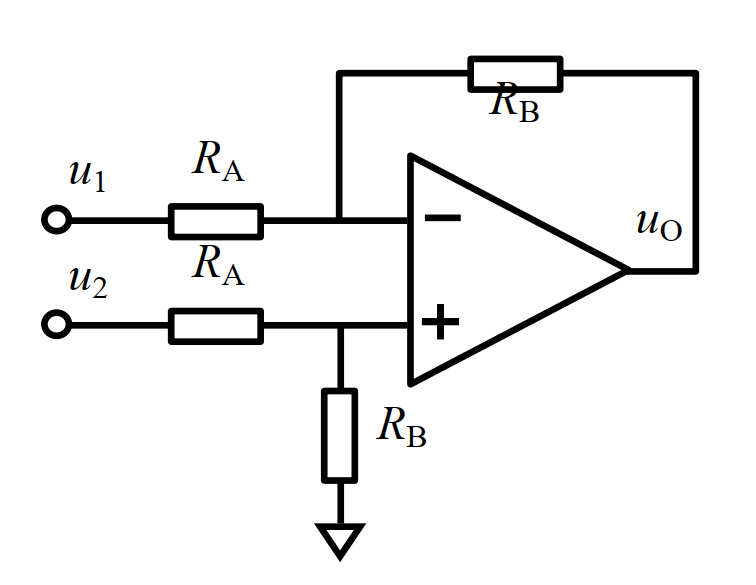
• Relation derivation ：$$U_{+}=\frac{R_B}{R_A+R_B}{u}_2=U_{-}$$$$i=\frac{u_1-U_{-}}{R_A}=\frac{U_{-}-u_o}{R_B}$$
• Jointly available ：$$u_o=\frac{R_B}{R_A}(u_2-u_1)$$
• Draw a simulation image , And set the magnification 250, The error signal to be collected is amplified 250 times .
  

integrator

• Integrator regulation ： The steady-state error is eliminated , Improve the accuracy . Because there are errors , Integral adjustment is done , Until there is no difference , Integral adjustment stop , The integrator outputs a constant . The strength of the integrator depends on the integration time constant σ,σ The smaller it is , The stronger the integral effect .σ The bigger it is , The weaker the integral , The dynamic response becomes slower when the integrator is added .
• Proportional regulation ： To react proportionally to the deviation of a system , There is a deviation in the system , The proportional adjustment immediately produces a regulating effect to reduce the deviation . It's a big proportion , It can speed up the adjustment , But too much of it , Reduce the stability of the system .
  

PWM Signal generator

• The comparator is DC/DC One of the common core modules in the converter , stay DC/DC The converter can not only be used as a separate module , It can also be used as a sub circuit of other modules . Do voltage comparator application , One end is connected to the signal of the error amplifier , The other end is connected to the sawtooth wave generated by the oscillator , The two are compared to produce a pulse width modulated signal , adopt PWM The signal controls the conduction and closing of the power switch tube .
• May refer to The principle of comparator

Improved complete circuit

• Simulation run , Get the following series of waveforms
  
• Output voltage waveform expansion , It can be seen that under the same electrolysis , The voltage ripple is greatly reduced , And basically close to 10V Output .