118. Yanghui triangle

Title Description

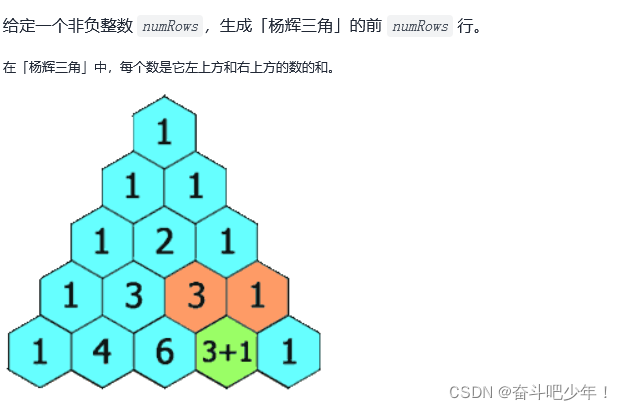
Their thinking

Solution 1 ： mathematics
Ideas ： There are two layers , Outermost list ret And the elements in the list （ It's also a list ）row. then , For each line of Yang Hui triangle , On both sides 1（j0 || j1）, The middle element , Use the previous line to correspond to the sum of the two elements （ret.get(i-1).get(j-1)+ret.get(i-1.get(j))）. Last , Add each row to ret in .
Time complexity ：O(numRows^2).
Spatial complexity ：O(1). Regardless of the space occupation of the return value

Code

 public static List<List<Integer>> generate(int numRows) {
    
            List<List<Integer>> ret = new ArrayList<List<Integer>>();
            for (int i = 0; i < numRows; ++i) {
    
                List<Integer> row = new ArrayList<Integer>();
                for (int j = 0; j <= i; ++j) {
    
                    if (j == 0 || j == i) {
    
                        row.add(1);
                    } else {
    
                        row.add(ret.get(i - 1).get(j - 1) + ret.get(i - 1).get(j));
                    }
                }
                ret.add(row);
            }
            return ret;
        }
}

link ：https://leetcode-cn.com/problems/pascals-triangle/solution/yang-hui-san-jiao-by-leetcode-solution-lew9/
source ： Power button （LeetCode）.