leetcode：1856. 子数组最小乘积的最大值

题目来源

• 1856. 子数组最小乘积的最大值

题目描述

给定一个只包含正数的数组arr，arr中任何一个子数组sub，一定都可以算出(sub累加和 )* (sub中的最小值)是什么，
那么所有子数组中，这个值最大是多少？

题目解析

题意

子数组是连续的。每一个子数组的累加和都可以算出来，这段数组的最小值也能求得，然后 A指标 = (sub累加和 )* (sub中的最小值)。

现在我们要求出当前数组中哪个子数组的A指标最大。

思考

问题：

• 以0位置的$3$作为最小值的子数组有哪些？
  • $[3]：3\ast 3=9$
  • $[3，4]：3\ast 7=21$，选它
• 以$1-->4$作为最小值的子数组有哪些？
  • $4：4\ast 4=16$
• 以$2-->2$作为最小值的子数组有哪些？
  • 得到：[3，4，2，3，4，6]$
    • 2尽量往左扩大，最多能扩到$[3，4，2$
    • 2尽量往右扩张，最大能扩到…2，3，4，6]
    • 为什么要尽量扩张，因为$指标A=sum\ast num$，指标A要尽量大，而num是固定的，所以sum应该尽量大
  • $[3，4，2，3，4，6]$含有$2$的所有子数组的指标A都会比2小
• 以$3-->3$作为最小值的子数组有哪些？
  • 。。。
• 以$4-->4$作为最小值的子数组有哪些？
  • 。。。
• 以$5-->6$作为最小值的子数组有哪些？
  • 。。。

第一个要解决的问题：

• 如何找出以$x$位置作为最小值的子数组的指标A最大呢？
  • x尽量往左看，找到比x更小的那个索引，假设为left
  • x尽量往右看，找到比x更小的那个索引，假设为right
  • 然后[left+1…right+1]这个区间范围内的所有数组全要，得到sum，然后sum * 2

第二个要解决的问题：求sum

• 用前缀和

注意，这里，单调栈不需要用链表。举个例子

（1）遍历数组，并入栈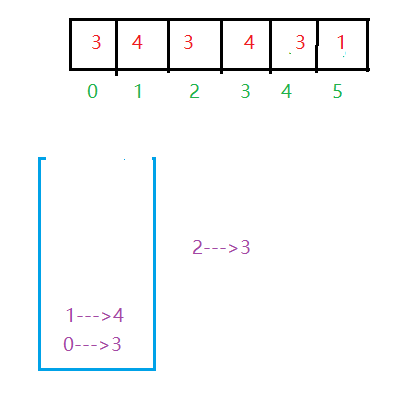

• 1—>4出栈，需要结算答案，得到
  • 1—>4：0—>3，2—>3
  • 也就是对于1—>4来说，它左扩不到0—>3位置，右扩不到2—>3，因此它只有它自己，{4}，得到4*4 = 16

那现在2—>3能入栈吗？不能，因为栈顶元素也是3，所以0—>3出栈：

• 0—>3出栈
  • 左边比我小的数：没有
  • 右边比我小的数：如果按照原来单调性的性质，应该是2—>3，但是实际上不对，应该是4—>3。怎么处理呢？
    • 无需处理，错了就错了，因为 0—>3和2—>3、4—>3是联通的，有朝一日会自动纠正的
    • 也就是说得到了子数组{3，4}，得到了7*3=21

现在栈变为：

继续遍历：

• 3—>4出栈：

  • 左边比 3—>4小的数：2—>3
  • 右边比 3—>4小的数：4—>3
  • 所以 3—>4向左扩到2—>3(不包括)为止，向右扩到4—>3(不包括)为止。得到子数组[4]，最终得到指标A=4*4=16

• 2–>3也需要出栈：

  • 左边比2–>3小的数：无
  • 右边比2–>3小的数：4—>3

继续遍历：5—>1可以入栈

5—>1可以入栈吗？不可以，为了满足栈单调增长，必须将4—>3出栈， 5—>1才能入栈

• 4—>3出栈
  • 右边比 4—>3小的数：5—>1，往右扩展到索引5(不包括)位置
  • 左边比4—>3小的数：没有，所以4—>3可以一直往左扩大，将索引4左边的所有数都放入到当前子数组中
  • 最终得到的子数组：[3、4、3、4、3]

小结：反正最后一个能算对，所以之前错了就错了，no care

实现