当前位置:网站首页>格林公式挖洞法中内曲线顺时针的直观解释
格林公式挖洞法中内曲线顺时针的直观解释
2022-06-23 22:16:00 【深海里的鱼(・ω<)*】
视频讲解:格林公式挖洞法中内曲线顺时针的直观解释
使用格林公式的时候,取曲线逆时针为正方向,但如果曲线包围的区域内存在奇点,则不能直接使用格林公式,需要先使用挖洞法,其中内曲线为顺时针,大家记忆口诀通常是“外逆内顺”,如图所示,A为平面上的奇点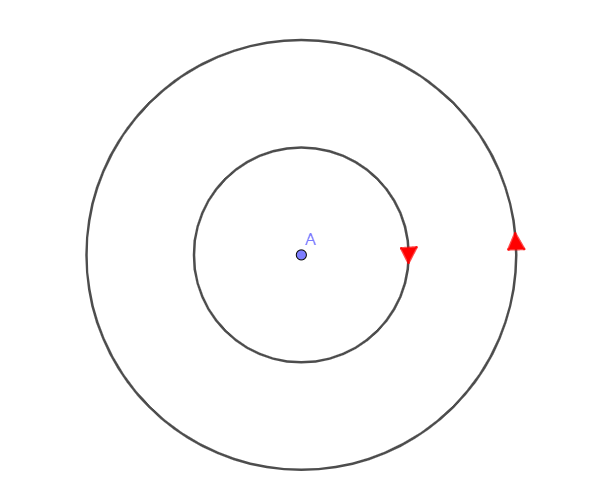
当然曲线可能并不像图示那么光滑,可能是凹凸不平,比如这样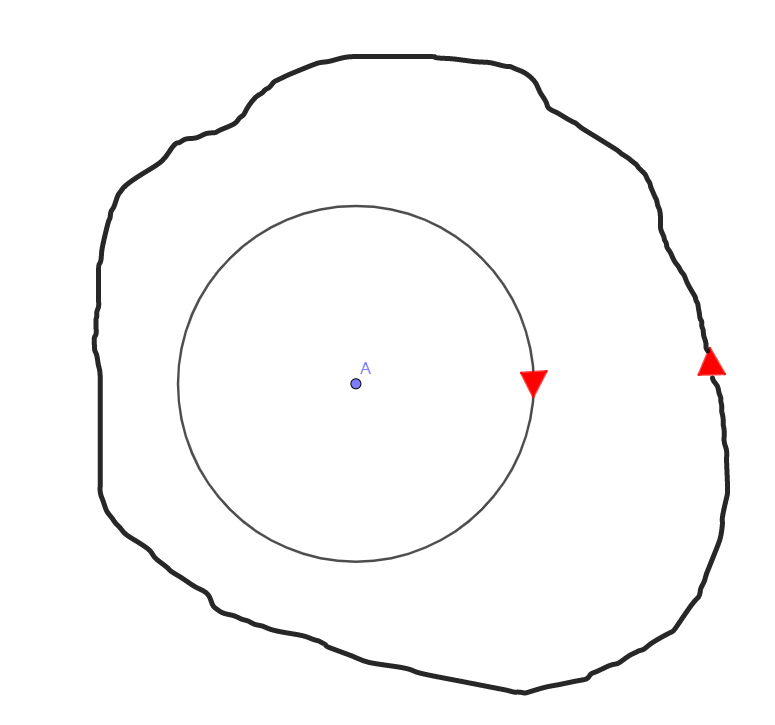
为了作图简单,本文将使用较为简单的曲面
那么为什么内曲线是顺时针呢,本文给大家一个直观的解释。
先来看一个这样的曲面,围成的区域为黄色部分,如图所示
此区域不包含奇点,所以可以放心的使用格林公式
∮ C = ∫ C 1 + ∫ l 1 + ∫ C 2 + ∫ l 2 = ∬ D \oint_C{}=\int_{C1}{}+\int_{l1}{}+\int_{C2}{}+\int_{l2}{}=\iint_D{} ∮C=∫C1+∫l1+∫C2+∫l2=∬D
我们将点B和C,点D和E逐渐靠近,直到重合,如图所示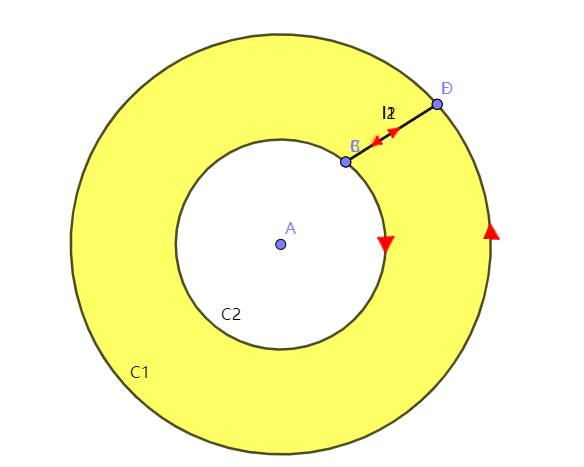
此时 l 1 l1 l1和 l 2 l2 l2重合,方向相反,则
∫ l 1 + ∫ l 2 = 0 \int_{l1}{}+\int_{l2}{}=0 ∫l1+∫l2=0
所以
∮ C = ∫ C 1 + ∫ l 1 + ∫ C 2 + ∫ l 2 = ∫ C 1 + ∫ C 2 = ∬ D \oint_C{}=\int_{C1}{}+\int_{l1}{}+\int_{C2}{}+\int_{l2}{}=\int_{C1}{}+\int_{C2}{}=\iint_D{} ∮C=∫C1+∫l1+∫C2+∫l2=∫C1+∫C2=∬D
所以我们可以将 l 1 l1 l1和 l 2 l2 l2去掉
所以最后可以得出
∮ C 1 + C 2 = ∬ D \oint_{C1+C2}{}=\iint_D{} ∮C1+C2=∬D
边栏推荐
猜你喜欢

19 MySQL optimizations commonly used in projects

Postman返回值中文乱码????

How to achieve the turning effect of wechat video recording?

2018/GAN:Self-Attention Generative Adversarial Networks自我注意生成对抗网络

项目中常用到的 19 条 MySQL 优化

MySQL索引底层为什么用B+树?看完这篇文章,轻松应对面试。

Some explanations of Tim timer of embedded interface and STM32 template library function of NVIC

【Proteus仿真】T6963C驱动PG12864示例(带中英文显示)
Task queue of laravel

ACM. HJ89 24点运算 ●●●
随机推荐
PyQt5_QTableWidget分页单选右键菜单控件
入参参数为Object,但传递过去却成了[object object] 是因为需要转为JSON格式
【Proteus仿真】T6963C驱动PG12864示例(带中英文显示)
【HackTheBox】 meow
Is the geTx status management in the flutter really so good to use?
AIX system monthly maintenance check (I)
Fabric. JS manual bold text iText
在OpenCloudOS使用snap安装.NET 6
7、STM32——LCD
CTF go topic recurrence
Analysis of Alibaba cloud Tianchi competition -- prediction of o2o coupon
Analysis on the advantages and disadvantages of the best 12 project management systems at home and abroad
Le roman du drapeau de l'imitation haute version flutter, apprenez - le
高仿书旗小说 Flutter 版,学起来
一款高仿腾讯漫画的漫画阅读类 APP
Facebook 开源微光效果 Shimmer
How can wechat video numbers be broadcast live on a PC?
PLC数据操作系列之构造不同应用场景的缓存栈FIFO(算法详解)
Stm32-------adc (voltage detection)
Sorry, your USB cable may be wrong!