当前位置:网站首页>[2013] [paper notes] terahertz band nano particle surface enhanced Raman——
[2013] [paper notes] terahertz band nano particle surface enhanced Raman——
2022-07-23 18:45:00 【Su Nianxin】
Preface
type
Terahertz + scattering Terahertz + scattering Terahertz + scattering
Periodical
Spectroscopy and spectral analysis Spectroscopy and spectral analysis Spectroscopy and spectral analysis
author
Wu Yudeng , Ren Guangjun , Hao Yun , Yaojianquan Wu Yudeng , Ren Guangjun , Hao Yun , Yaojianquan Wu Yudeng , Ren Guangjun , Hao Yun , Yaojianquan
Time
2013 2013 2013
Catalog
\;\\\;\\\;
Surface enhanced Raman scattering SERS
When material molecules are adsorbed on some specific metal surfaces , The Raman scattering intensity of molecules will be greatly enhanced
( The enhancement factor can reach 1 0 3 ∼ 1 0 7 10^3\sim 10^7 103∼107)
For nano scale rough surfaces , The enhancement of the signal can reach a million billion times
\;\\\;\\\;
Raman scattering
The frequency of light wave changes after being scattered
\;\\\;\\\;
Electromagnetic enhancement
Surface plasmon resonance SPR Local electromagnetic field enhancement caused
\;\\\;\\\;
Chemical enhancement
There is charge transfer between the substrate and the adsorbed material
Mainly due to The polarizability of molecules adsorbed on rough surfaces changes The enhancement of Raman signal caused by .
\;\\\;\\\;
research objective
1 Terahertz + Combination of low frequency Raman spectra
Intermolecular and intramolecular low-frequency stretching of some macromolecules 、 Bending vibration , Lattice phonon vibration , Hydrogen bond stretching 、 Torsional vibration
—— The corresponding absorption frequencies are distributed in THz Band
- Terahertz has great application prospects in the detection of macromolecules
But macromolecules THz Research Absorption frequency
Low frequency Raman spectroscopy can reflect the vibration characteristics of macromolecules
SERS Surface enhanced Raman scattering can make THz Combined with low-frequency Raman spectroscopy
\;\\\;\\\;
2 explain SERS
Is there anything else (2013) A complete theoretical explanation SERS( Surface enhanced Raman scattering ) Enhancement mechanism of
Recognized mechanism :
Based on surface plasmon theory Electromagnetic enhancement Mechanism + Based on charge transfer theory Chemical enhancement Mechanism
\;\\\;\\\;
Research methods
Electromagnetic enhancement : Including the surface plasma model 、 Antenna resonator model 、 Mirror field model
Based on the above model, we can use FDTD Finite difference time domain , The simple results are simulated accurately
FDTD There are different expressions in different media
This paper discusses the surface strengthening effect of metal nanoparticles
Mesh scale : 0.5 n m × 0.5 n m 0.5nm\times 0.5nm 0.5nm×0.5nm
The number of grids : 200 × 200 200\times 200 200×200
Nanoparticles : gold Au Nanoparticles
Model : Plane model
Particle size : 20 n m 20nm 20nm
Incident wave : Plane linearly polarized wave
For different sizes of two particles 、 Simulate with different spacing
\;
\;
\;
Research models
Metal nanoparticles are dispersive , use Drude The function represents its relative dielectric constant :
ε ( ω ) = 1 + ω p 2 ω ( i ν c − ω ) = 1 + χ ( ω ) \varepsilon(\omega) = 1 + \frac{\omega_p^2}{ \omega ( i \nu _c - \omega ) } = 1+ \chi (\omega) ε(ω)=1+ω(iνc−ω)ωp2=1+χ(ω)
among ω p \omega_p ωp Is the plasma frequency of dispersive medium , ν c \nu_c νc Is the plasma collision frequency of dispersive medium
\;
Dispersive medium , Time domain
D ( t ) = ε ∞ ε 0 E ( t ) + ε 0 ∫ 0 t E ( t − τ ) ⋅ χ ( τ ) d τ D(t)=\varepsilon_{\infty} \varepsilon _0 E(t) + \varepsilon_0 \int_0^tE(t - \tau) \cdot \chi(\tau)d\tau D(t)=ε∞ε0E(t)+ε0∫0tE(t−τ)⋅χ(τ)dτ
among χ ( τ ) \chi(\tau) χ(τ) Is the inverse Fourier transform of the polarization rate , ε ∞ \varepsilon_{\infty} ε∞ yes ω → ∞ \omega \rightarrow \infty ω→∞ The relative permittivity of
\;
Yee Coriolis grid
Use Yee The time is discretized by T-grid , t = n Δ t t=n\Delta t t=nΔt, be
D ( t ) ≈ D ( n Δ t ) = D n = ε ∞ ε 0 E n + ε 0 ∫ 0 n Δ t E ( n Δ t − τ ) ⋅ χ ( τ ) d τ D(t) \approx D(n\Delta t)=D^n=\varepsilon_{\infty} \varepsilon _0 E^n + \\\\\varepsilon_0\int_0^{n\Delta t}E(n\Delta t - \tau) \cdot \chi(\tau)d\tau D(t)≈D(nΔt)=Dn=ε∞ε0En+ε0∫0nΔtE(nΔt−τ)⋅χ(τ)dτ
When t < 0 t<0 t<0 when , D ( t ) = E ( t ) = 0 D(t)=E(t)=0 D(t)=E(t)=0
Take the field value of each step as a constant , Yes
D n = ε ∞ ε 0 E n + ε 0 ∑ m = 0 n − 1 E n − m ⋅ ∫ m Δ t ( m + 1 ) Δ t χ ( τ ) d τ D^n=\varepsilon_{\infty} \varepsilon _0 E^n + \varepsilon_0\sum_{m=0}^{n-1}E^{n-m}\cdot \int_{m\Delta t}^{ (m+1)\Delta t } \chi(\tau)d\tau Dn=ε∞ε0En+ε0m=0∑n−1En−m⋅∫mΔt(m+1)Δtχ(τ)dτ
D n + 1 = ε ∞ ε 0 E n + 1 + ε 0 ∑ m = 0 n E n − m + 1 ⋅ ∫ m Δ t ( m + 1 ) Δ t χ ( τ ) d τ D^{n+1}=\varepsilon_{\infty} \varepsilon _0 E^{n+1} + \varepsilon_0\sum_{m=0}^{n}E^{n-m + 1}\cdot \int_{m\Delta t}^{ (m+1)\Delta t } \chi(\tau)d\tau Dn+1=ε∞ε0En+1+ε0m=0∑nEn−m+1⋅∫mΔt(m+1)Δtχ(τ)dτ
\;
Isotropic metal medium
For isotropic metallic media , Yes
∇ × H = ∂ D / ∂ t ∇ × E = ∂ B / ∂ t B = μ H D = ε H \nabla \times H ={\partial D}/{\partial t} \\\\ \nabla \times E = {\partial B}/{\partial t} \\\\B=\mu H \\\\ D=\varepsilon H ∇×H=∂D/∂t∇×E=∂B/∂tB=μHD=εH
among μ and ε \mu and \varepsilon μ and ε They are the permeability and dielectric constant of dispersive medium
according to Yee Grid definition x = i Δ x , y = i Δ y , t = n Δ t x=i\Delta x, y=i\Delta y, t=n\Delta t x=iΔx,y=iΔy,t=nΔt, take D n And D n + 1 D^n And D^{n+1} Dn And Dn+1 Substituting into dispersive medium maxwell Fang Chengzhong , The electric field difference equation of dispersive medium is obtained :
E x n , s ( i , j ) = ε ∞ ε 0 ε ∞ ε 0 + σ Δ t + ε 0 χ 0 E x n − 1 , s ( i , j ) − σ Δ t ε ∞ ε 0 + σ Δ t + ε 0 χ 0 E x n , i ( i , j ) + ε 0 ε ∞ ε 0 + σ Δ t + ε 0 χ 0 Ψ x n ( i , j ) − ( ε ∞ − 1 ) ε 0 Δ t ε ∞ ε 0 + σ Δ t + ε 0 χ 0 ∂ E x n , i ( i + 1 / 2 , j ) ∂ t − ε 0 Δ t ε ∞ ε 0 + σ Δ t + ε 0 χ 0 ∂ ∂ t ∫ 0 n E x i ( t − τ ) χ ( τ ) d τ + Δ t ε ∞ ε 0 + σ Δ t + ε 0 χ 0 [ H z n − 1 / 2 , s ( i , j ) − H z n − 1 / 2 , s ( i , j − 1 ) Δ y ] E_x^{n,s}(i,j) = \frac{\varepsilon_{\infty} \varepsilon _0 }{ \varepsilon_{\infty} \varepsilon _0 + \sigma \Delta t + \varepsilon_0 \chi^0 } E_x^{n-1,s}(i,j) - \\\\ \frac{\sigma\Delta t}{\varepsilon_{\infty} \varepsilon _0 + \sigma \Delta t + \varepsilon_0 \chi^0} E_x^{n,i}(i,j) + \\\\ \frac{\varepsilon_0}{\varepsilon_{\infty} \varepsilon _0 + \sigma \Delta t + \varepsilon_0 \chi^0}\Psi _x^n(i,j ) - \\\\ \frac{( \varepsilon_{\infty} - 1 )\varepsilon_0 \Delta t }{\varepsilon_{\infty} \varepsilon _0 + \sigma \Delta t + \varepsilon_0 \chi^0} \frac{ \partial E_x^{n,i}(i+1/2,j) }{\partial t} - \\\\ \frac{ \varepsilon_0 \Delta t}{ \varepsilon_{\infty} \varepsilon _0 + \sigma \Delta t + \varepsilon_0 \chi^0 } \frac{\partial }{\partial t} \int_0^n E_x^i(t-\tau)\chi(\tau) d\tau + \\\\ \frac{ \Delta t }{ \varepsilon_{\infty} \varepsilon _0 + \sigma \Delta t + \varepsilon_0 \chi^0} [ \frac{H^{n-1/2,s}_z(i,j) - H^{n-1/2,s}_z(i,j-1)}{ \Delta y } ] Exn,s(i,j)=ε∞ε0+σΔt+ε0χ0ε∞ε0Exn−1,s(i,j)−ε∞ε0+σΔt+ε0χ0σΔtExn,i(i,j)+ε∞ε0+σΔt+ε0χ0ε0Ψxn(i,j)−ε∞ε0+σΔt+ε0χ0(ε∞−1)ε0Δt∂t∂Exn,i(i+1/2,j)−ε∞ε0+σΔt+ε0χ0ε0Δt∂t∂∫0nExi(t−τ)χ(τ)dτ+ε∞ε0+σΔt+ε0χ0Δt[ΔyHzn−1/2,s(i,j)−Hzn−1/2,s(i,j−1)]
among
Ψ x n ( i , j ) = E s n ( i , j ) Δ χ 0 + Ψ x n − 1 ( i , j ) e − ν c Δ t \Psi_x^n(i,j)= E_s^n(i,j)\Delta \chi^0 + \Psi_x^{n-1}(i,j) e^{ - \nu_c \Delta t } Ψxn(i,j)=Esn(i,j)Δχ0+Ψxn−1(i,j)e−νcΔt
χ 0 = ω p 2 ν c Δ t − ( ω p ν c ) 2 [ 1 − e − ν c Δ t ] \chi^0=\frac{ \omega_p^2 }{ \nu_c }\Delta t - ( \frac{ \omega_p }{\nu_c} )^2 [1 - e^{-\nu_c\Delta t}] χ0=νcωp2Δt−(νcωp)2[1−e−νcΔt]
Δ χ m = − ( ω p ν c ) 2 e − m ν c Δ t [ 1 − e − ν c Δ t ] 2 \Delta \chi^m=-( \frac{ \omega_p }{\nu_c} )^2 e^{ - m \nu_c \Delta t}[ 1 - e^{-\nu_c\Delta t} ]^2 Δχm=−(νcωp)2e−mνcΔt[1−e−νcΔt]2
χ ( τ ) = ω p 2 ν c [ 1 − e − ν c τ ] U ( τ ) \chi(\tau)=\frac{ \omega_p^2 }{ \nu_c }[ 1 - e^{-\nu_c\tau} ]U(\tau) χ(τ)=νcωp2[1−e−νcτ]U(τ)
Through the above analysis, free space 、 Perfect matching layer 、 The surface electromagnetic enhancement of nanoparticles is simulated by setting dispersive media respectively
\;\\\;\\\;
Analysis of simulation results
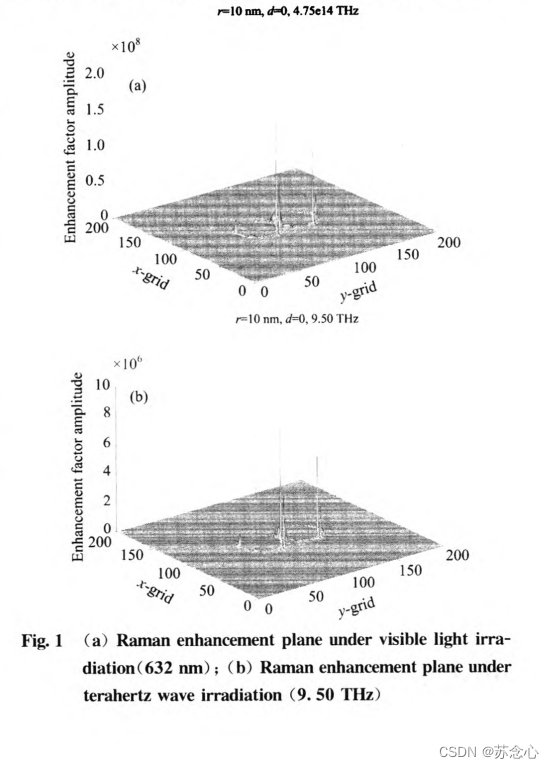
Sure ? See the plane wave incident spectral enhancement factor ( ∣ E E 0 ∣ 2 |\frac{E}{E_0}|^2 ∣E0E∣2) Concentrated at the junction and edge of the two nanoparticles , The enhancement of the junction reflects Interaction of nanoparticles under light wave irradiation Influence on the spectrum
\;\\\;\\\;
Conclusion
By changing the different parameters of metal nanoparticles , Under the irradiation of terahertz wave , Different electromagnetic enhancement effects are obtained
- It is proved that terahertz wave also has electromagnetic enhancement effect on the surface of metal nanoparticles
bring Surface enhanced Raman scattering SERS, From visible light + The infrared band is extended to THz Band
bring SERS Combined with terahertz wave Make it possible (2013)
\;\\\;\\\;
problem
2022 Year now ,SERS And THz How is the combination ? What are the results ?
Right now SERS Has the reason for the mechanism been modified ?
Chemical enhancement and THz What are the combined results ?
\;\\\;\\\;
边栏推荐
- How to capture the analyst rating data of Sina Financial Data Center?
- 次世代行业现状如何?90%转行建模师都在学习这套流程
- What happened behind kubectl's creation of pod?
- How to evaluate the accuracy of stock analysts' prediction?
- Installation and use of flame graphs
- [attack and defense world web] difficulty four-star 12 point advanced question: cat
- MySQL performance tuning
- 银行业如何实现数字化转型风口全速启航
- 使用kail破解wifi密码
- Alliance DAO创始人:100+Web3基础设施及Dapp创业清单
猜你喜欢

Rhcsa notes 7

银行业如何实现数字化转型风口全速启航

Problems and methods of creating multiple projects under one solution in VS2010

Is 3D modeling promising? Is employment guaranteed with high salary or is it more profitable to take orders in sideline industry
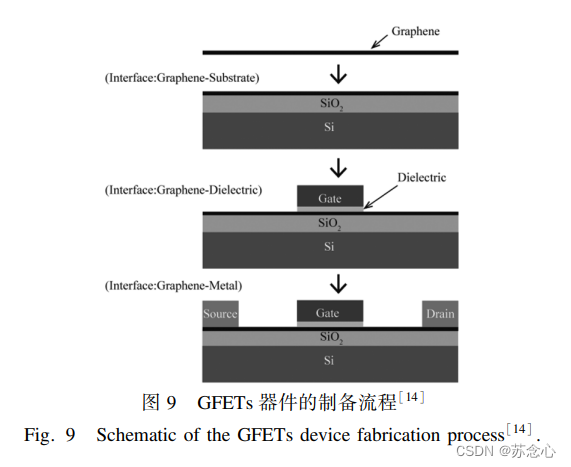
【2018】【论文笔记】石墨烯场效应管及【2】——石墨烯的制备、转移

LM393低功耗双电压比较器参数、引脚、应用详解

Is it suitable for learning 3D modeling? You can't lose one of these five points

Where should we start to learn modeling from zero foundation? How to learn game modeling well?

How does Apache, the world's largest open source foundation, work?

Installation and use of flame graphs
随机推荐
Redis [2022 latest interview question]
PCL:多直线拟合(RANSAC)
MQ【MessageQueue 图文详解及四大MQ比较】
我的创作纪念日
PCL: ajustement multiligne (RANSAC)
The original path is not original [if there is infringement, please contact the original blogger to delete]
OSI模型第一层:物理层,基石般的存在!
【游戏建模模型制作技巧分享】ZBrush如何调整笔刷大小
Stack / heap / queue question brushing (medium)
怎么将word中的times new roman的双引号替换成宋体双引号
Redis【超强超细 入门教程】
【游戏建模模型制作全流程】用ZBrush制作游戏士兵角色
SQLZOO——SELECT from Nobel Tutorial
Interface test overview
【2020】【论文笔记】基于二维光子晶体的光控分光比可调Y——
String length function strlen().. String function header file string.h "suggestions collection"
知乎二面:请问Redis 如何实现库存扣减操作和防止被超卖?
Can self-study 3D modeling succeed? Can self-study lead to employment?
BOM introduction of BOM series
【重磅】聚焦券商终端业务,博睿数据发布新一代券商终端核心业务体验可观测平台